一元线性回归模型参数的最小二乘估计方法

（一）回归系数的点估计

所谓最小二乘法就是通过使残差平方和为最小来估计回归系数的一种方法。

将Q对和求偏导数，并令其等于零，可得

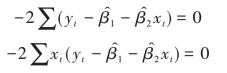
加以整理后有

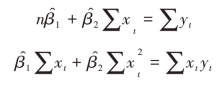
以上方程组称为正规方程组或标准方程组，式中的n是样本容量。求解这一方程组可得：

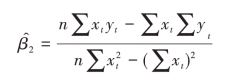
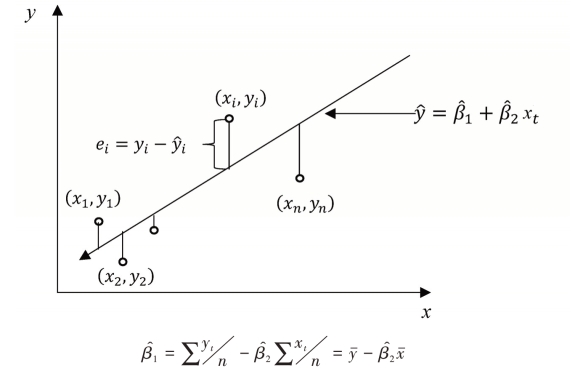
图6-7　回归模型估计

（二）最小二乘估计量的性质

按照最小二乘法求得的估计总体回归系数的数学公式是样本观测值的函数，通常称之为最小二乘估计量。

可以证明，在标准假定能够得到满足的条件下，回归系数的最小二乘估计量的期望值等于其真值，即有：

其方差为：

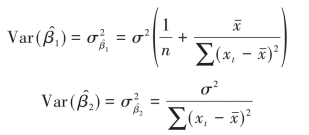
（三）总体方差的估计

除了β1和β2之外，一元线性回归模型还包括了一个未知参数，那就是总体随机误差项的方差s2，它反映理论模型误差的大小，由于随机误差项本身是不能直接观测的，因此，需要用最小二乘残差代替随机误差项来估计s2。(www.xing528.com)

数学上可以证明，s2的无偏估计S2可由下式给出：

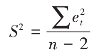
式中，分子是残差平方和，分母是自由度，其中n是样本观测值的个数，2是一元线性回归方程中回归系数的个数。S又叫作回归估计的标准误差。

一般采用以下公式计算残差平方和：

【例6-5】下表是2000—2019年我国城镇居民人均年消费性支出和人均年可支配收入的有关资料，我们利用表中已给出我国历年城镇居民人均消费支出和人均可支配收入的数据，来估计我国城镇居民的边际消费倾向和基础消费水平。

表6-5　2000—2019年我国城镇居民人均年消费性支出和人均年可支配收入

续表6-5

解：

样本回归方程为：=0.1214+0.6425xt

上式中：0.6425是边际消费倾向，表示人均可支配收入每增加1万元，人均消费支出会增加0.6425万元；0.1214是基本消费水平，即与收入无关最基本的人均消费为1214元。

【例6-6】根据例6-5中给出的有关数据和已得到的回归系数估计值，计算我国城镇居民消费函数的总体方差S2和回归估计标准差S。

解：根据例6-5中给出的有关数据和已得到的回归系数估计值，可得：

进而有：S=0.012546