一元线性回归模型在《统计学原理》中的标准

（一）总体回归模型

Yt=β1+β2 Xt+ut

上式被称为总体回归模型。式中的β1和β2是未知的参数，又叫回归系数。其中，Yt和Xt分别是Y和X的第t个观测值。ut是随机误差项，又称随机干扰项，它是一个特殊的随机变量，反映未列入方程式的其他各种因素对Y的影响。随机扰动项ut包含了丰富的内容，产生的原因主要有以下几个方面：

（1）忽略掉的影响因素造成的误差；

（2）模型关系不准确造成的误差；

（3）变量观测值的计量误差；

（4）随机误差。

（二）误差项的标准假定

假定1：误差项的期望值为0，即对所有的t总有

E(ut)=0

假定2：误差项的方差为常数，即对所有的t总有

Var(ut)=E(u2t)=σ2

假定3：误差项之间不存在序列相关关系，其协方差为零，即当t≠s时有：

Cov(ut,us)=0

假定4：自变量是给定的变量，与误差项线性无关。

假定5：随机误差项服从正态分布。

满足以上标准假定的一元线性模型，称为标准的一元线性回归模型。(www.xing528.com)

描述Y的平均值或期望值如何依赖于X的方程称为回归方程（回归函数），一元线性回归方程（回归函数）的形式如下：

E(Yt)=β1+β2 Xt

方程的图示是一条直线，也称为直线回归方程。β1是回归直线在Y轴上的截距，是当X=0时Y的期望值；β2是直线的斜率，称为回归系数，表示当X每变动一个单位时，X的平均变动值。

图6-6　回归方程

（三）样本回归函数

在现实问题研究中，由于所要研究的现象的总体单位数一般是很多的，在许多场合甚至是无限的，因此无法掌握因变量Y总体的全部取值。也就是说，总体回归函数事实上是未知的，需要利用样本的信息对其进行估计。一元线性回归函数的样本回归函数（回归方程）可表示为：

式中的是样本回归线上与xt相对应的y值，可视为E（Yt）的估计；是样本回归函数的截距系数，是样本回归函数的斜率系数，它们是对总体回归系数β1和β2的估计。

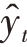实际观测到的因变量yt值，并不完全等于如果用et表示二者之差（et=yt-），则有：

上式称为样本回归模型。式中et称为残差。

样本回归函数与总体回归函数之间的区别。

（1）总体回归线是未知的，它只有一条。而样本回归线则是根据样本数据拟合的，每抽取一组样本，便可以拟合一条样本回归线。

（2）总体回归模型中的β1和β2是未知的参数，表现为常数。而样本回归模型中的和是随机变量，其具体数值随所抽取的样本观测值不同而变动。

（3）总体回归模型中的ut是Yt与未知的总体回归线之间的纵向距离，它是不可直接观测的。而样本回归模型中的et是yt与样本回归线之间的纵向距离，当根据样本观测值拟合出样本回归线之后，可以计算出et的具体数值。