统计学原理：相关分析的描述与测度

相关分析一般可以借助于相关表、相关图或相关系数来进行。

（一）相关表

相关表是一种反映变量之间相关关系的统计表。

【例6-1】假设对10户居民家庭的月可支配收入和消费支出进行调查，得到原始资料如表6-1。

表6-1　10户居民家庭的月可支配收入和消费支出

根据以上原始资料，将消费支出按从小到大的顺序排列，可编制相关表如表6-2。

表6-2　月可支配收入和消费支出相关表

由上表可见，消费支出与月可支配收入之间存在比较强的正相关关系。

（二）相关图

相关图又称散点图。它是以直角坐标系的横轴代表变量X，纵轴代表变量Y，将两个变量间相对应的变量值用坐标点的形式描绘出来，用来反映两变量之间相关关系的图形。

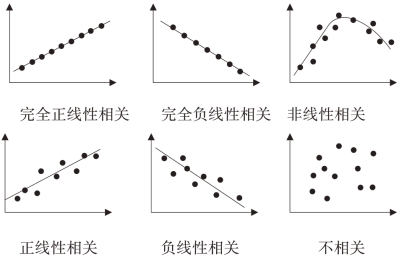
图6-2　相关图

利用相关图可以更直观、更形象地表现变量之间相关关系的方向、形式和强度。如果两个变量是正相关的，则相关图中的点呈由左到右向上倾斜；如果两个变量是负相关的，则相关图中的点呈由左到右向下倾斜。

观察相关图，要寻找整体形态以及明显偏离整体形态的偏差。要描述相关图的整体形态，可以描述点的形式、方向及相关关系的强度；一种重要形式的偏差是异常值，也就是落在相关关系的整体形态之外的个别值。

【例6-2】一家大型商业银行在多个地区设有分行，其业务主要是进行基础设施建设、国家重点项目建设、固定资产投资等项目的贷款。近年来，该银行的贷款额平稳增长，但不良贷款额也有较大比例的增长，这给银行业务的发展带来较大压力。为弄清楚不良贷款形成的原因，管理者希望利用银行业务的有关数据做些定量分析，以便找出控制不良贷款的办法。下面是该银行所属的25家分行的有关业务数据。

表6-3　25家分行的有关业务数据

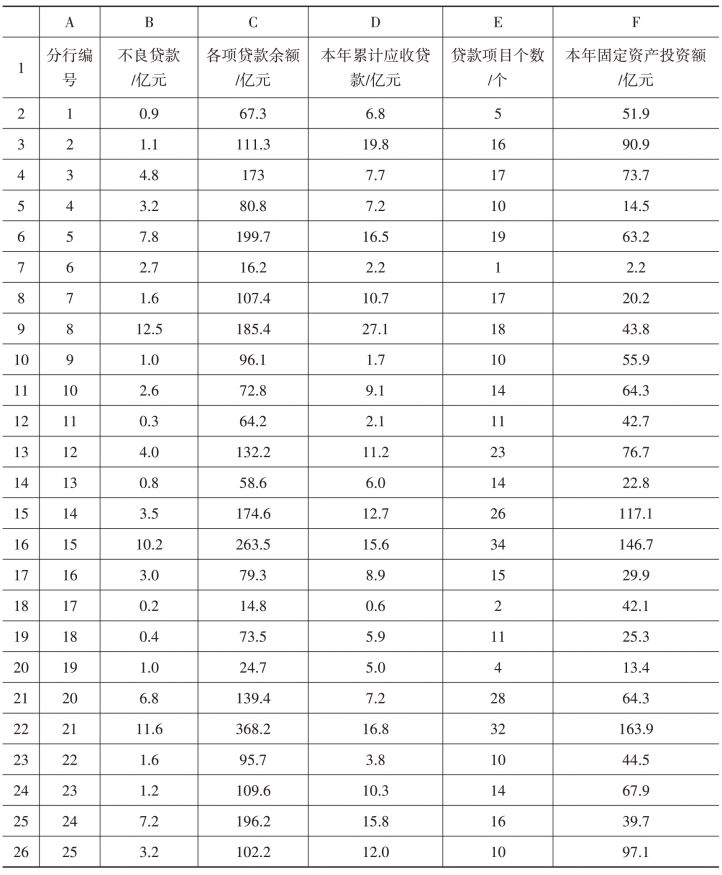
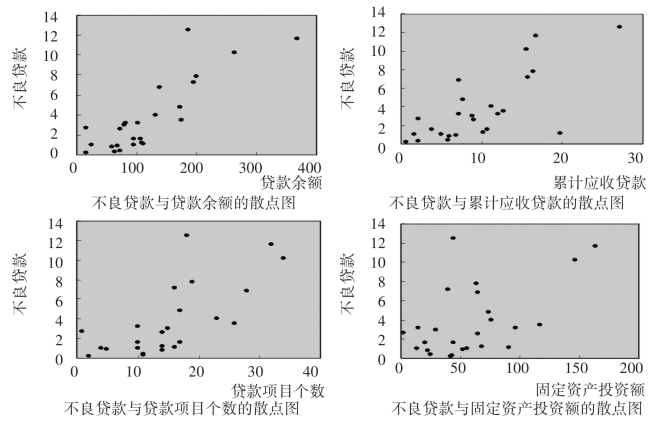
图6-3　各变量之间相关图

单纯用眼睛来观察相关图有时候不容易判断相关性的强弱。本来是同样的一组数据，只要图中坐标轴上的刻度不同，或者图中点和点之间的空白大小不同，肉眼观察的结果就可能受骗，从而得出相关程度不同的结论。所以我们得遵照数据分析的一般策略，除了图以外还要加上数值度量。相关系数就是我们要用的度量指标。

（三）相关系数

1.相关系数是度量变量之间关系强度的一个统计量。

2.对两个变量之间线性相关强度的度量称为简单相关系数。

3.若相关系数是根据总体全部数据计算的，称为总体相关系数，记为γ。

4.若是根据样本数据计算的，则称为样本相关系数，简称为相关系数，记为r，也称为线性相关系数（linear correlation coefficient）或称为Pearson相关系数（Pearson’s correlation coefficient）。

1.相关系数的定义

总体相关系数的定义式是

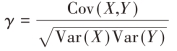
总体相关系数是反映两变量之间线性相关程度的一种特征值，表现为一个常数，一般是不知道的。

样本相关系数的定义公式是

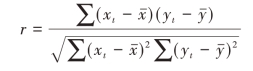
上式中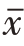，和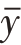分别是x和y的样本平均数。

样本相关系数是根据样本观测值计算的，抽取的样本不同，其具体的数值也会有所差异。样本相关系数是总体相关系数的一致估计量。

2.相关系数的性质

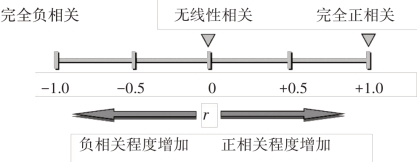
性质1：r的取值范围是[-1，1]，介于-1与1之间。

|r|=1，为完全相关；r=1，为完全正相关；r=-1，为完全负相关；r=0，不存在线性相关关系。

-1≤r＜0，为负相关；0＜r≤1，为正相关。

|r|越趋于1表示关系越强；|r|越趋于0表示关系越弱。

(www.xing528.com)

图6-4　相关系数的性质1

性质2：r具有对称性。即x与y之间的相关系数和y与x之间的相关系数相等，即rxy=ryx。

性质3：r数值大小与x和y原点及尺度无关，即改变x和y的数据原点及计量尺度，并不改变r数值大小。

性质4：r仅仅是x与y之间线性关系的一个度量，它不能用于描述非线性关系。这意味着，r=0只表示两个变量之间不存在线性相关关系，并不说明变量之间没有任何关系。

性质5：r虽然是两个变量之间线性关系的一个度量，却不一定意味着x与y一定有因果关系。

性质6：相关系数和平均数与标准差一样，也会受到少数异常观测值的严重影响。因此，当相关图中出现异常点时，使用相关系数要特别小心。

例如：对于变量1和变量2的如下取值：

变量1：38 56 59 64 74

变量2：41 63 70 72 84

相关系数为0.944，但如果将变量1的38改成60，则两变量的相关系数就将降为0.640。

性质7：由相关系数所反映出来的相关不一定是真实存在的，也有可能是虚假的。需要结合有关理论知识进行判断。

3.相关系数的经验解释

（1）|r|≥0.8时，可视为两个变量之间高度相关；

（2）0.5≤|r|＜0.8时，可视为中度相关；

（3）0.3≤|r|＜0.5时，可视为低度相关；

（4）|r|＜0.3时，说明两个变量之间的相关程度极弱，可视为不相关。

上述解释必须建立在对相关系数的显著性进行检验的基础之上。

4.相关系数的计算

具体计算样本相关系数时，通常利用以下公式：

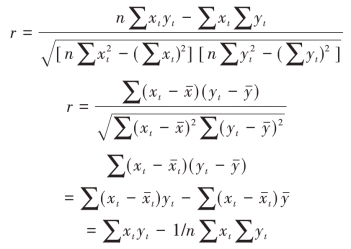
【例6-3】下表是2000—2019年我国城镇居民人均消费性支出和人均可支配收入的有关资料，试计算消费性支出与可支配收入的样本相关系数。

表6-4　2000—2019年我国城镇居民人均消费性支出和人均可支配收入

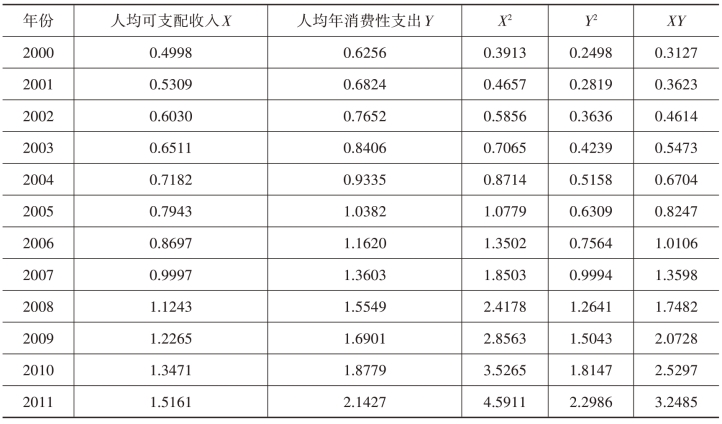
续表6-4

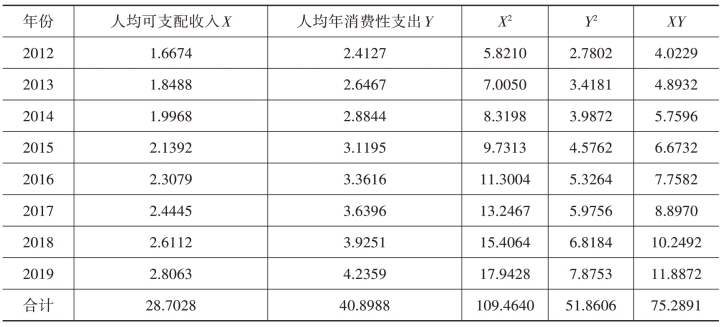
消费性支出与可支配收入的样本相关系数

当用样本相关系数估计总体相关系数时，其估计结果的准确性受样本量大小的影响（作为极端情形，样本量为2时，相关系数将为1，但实际上这可能是不正确的），也与所抽到的具体样本有关。

由于样本相关系数是一个随所抽到的具体样本而变动的随机变量，所以，就存在这样一个问题：由样本相关系数出发对总体相关系数的估计结果是否为抽样的偶然结果呢？为此，需要对相关系数的统计显著性进行检验。

5.相关系数的显著性检验

检验两个变量之间是否存在线性相关关系，也就是对总体相关系数g是否等于0进行检验。

检验的步骤为：

（1）提出假设：H0：g=0；H1：g1=0。

（2）计算检验的统计量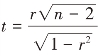，该统计量是服从自由度为（n-2）的t分布。

（3）根据给定的显著性水平a和自由度（n-2），查找t分布表中相应的临界值ta/2。若|t|≥ta/2，表明r在统计上是显著的，应拒绝原假设H0。若|t|≤ta/2，表明r在统计上是不显著的，应接受原假设H0。

【例6-4】假设根据6对样本观测数据计算出某公司的股票价格与气温的样本相关系数r=0.5，试问是否可以根据5%的显著水平认为该公司的股票与气温之间存在一定程度的线性相关关系？

解：H0：g=0；H1：g≠0

r的t检验值

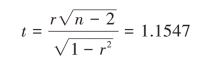
查表可知：

显著水平为5%、自由度为4的临界值ta/2=2.776，上式中的t值小于2.776，因此，r不能通过显著性检验。这就是说，尽管根据样本观测值计算的r达到0.5，但是由于样本单位过少，这一结论并不可靠，它不足以证明该公司的股票与气温之间存在一定程度的线性相关关系。