《统计学原理》中的假设检验流程

通过上面的引例，我们可以总结出假设检验的流程：

§ 提出假设

§ 确定适当的检验统计量并计算检验统计量的值

§ 规定显著性水平a

§ 做出统计决策

1.提出假设：原假设与备择假设。

原假设一般用H0表示，原假设是建立在假定原来总体没有发生变化的基础之上的，也就是总体参数没有显著变化。备选假设是原假设的对立，是在否认原假设之后所要接受的内容，通常这是我们真正感兴趣的一个判断，原假设与备择假设不可能同时成立。所谓假设检验问题实质上就是要判断H0是否正确，若拒绝原假设H0，则意味着接受备择假设H1。

如在引例中，我们可以提出两个假设：假设平均袋装咖啡质量与所要控制的标准没有显著差异，记为H0：m=150；假设平均袋装咖啡质量与所要控制的标准有显著差异，记为H1：m≠150。

根据假设的形式：双侧检验与单侧检验（表5-1）：

表5-1　假设的形式

假设检验中的两类错误：

显著性检验中的第一类错误是指：原假设事实上正确，可是检验统计量的观测值却落入拒绝域，因而否定了本来正确的假设。这是弃真的错误。发生第一类错误的概率a在双侧检验时是两个尾部的拒绝域面积之和；在单侧检验时是单侧拒绝域的面积。

显著性检验中的第二类错误是指：原假设事实上不正确，而检验统计量的观测值却落入了不能拒绝域，因而没有否定本来不正确的原假设，这是取伪的错误。发生第二类错误的概率是把来自θ=θ1（θ1≠θ0）的总体的样本值代入检验统计量所得结果落入接受域的概率b。

根据不同的检验问题，对于a和b大小的选择有不同的考虑。例如，在引例中，如果检验者站在卖方的立场上，他较为关心的是不要犯第一类错误，即不要发生产品本来合格却被错误地拒收这样的事情，这时，a要较小。反之，如果检验者站在买者的立场上，他关心的是不要把本来不合格的产品误当作合格品收下，也就是说，最好不要犯第二类错误，因此，b要较小。

在样本容量n不变的条件下，犯两类错误的概率常常呈现反向的变化，要使a和b都同时减小，除非增加样本的容量。为此，统计学家奈曼与皮尔逊提出了一个原则，即在控制犯第一类错误的概率a情况下，尽量使犯第二类错误的概率b小。在实际问题中，我们往往把要否定的陈述作为原假设，而把拟采纳的陈述本身作为备择假设，只对犯第一类错误的概率a加以限制，而不考虑犯第二类错误的概率b。

2.确定适当的检验统计量

所谓检验统计量，就是根据所抽取的样本计算的用于检验原假设是否成立的随机变量。检验统计量中应当含有所要检验的总体参数，以便在“总体参数等于某数值”的假定下研究样本统计量的观测结果。检验统计量还应该在“H0成立”的前提下有已知的分布，从而便于计算出现某种特定的观测结果的概率。

选择统计量的方法与参数估计相同，需考虑是大样本还是小样本，总体方差已知还是未知。

3.规定显著性水平a

在假设检验中，我们做出判断时所依据的逻辑是：如果在原假设正确的前提下，检验统计量的样本观测值的出现属于小概率事件，那么可以认为原假设不可信，从而否定它，转而接受备择假设。

至于小概率的标准是多大，这要根据实际问题而定。假设检验中，称这一标准为显著性水平，用来表示a，在应用中，通常取a=0.01，或a=0.05。一般来说，犯第一类错误可能造成的损失越大，a的取值应当越小。

4.做出决策

对假设检验问题做出判断可依据两种规则：一是P值规则；二是临界值规则。

什么是P值？（P value），它是一个概率值。

（一）P值规则

所谓P值，实际上是检验统计量超过（大于或小于）具体样本观测值的概率。如果P值小于所给定的显著性水平，则认为原假设不太可能成立；如果P值大于所给定的标准，则认为没有充分的证据否定原假设。

双侧检验的P值（图5-3）

图5-3　双侧检验的P值

左侧检验的P值（图5-4）

图5-4　左侧检验的P值

右侧检验的P值（图5-5）(www.xing528.com)

图5-5　右侧检验的P值

利用P值进行检验进行决策的准则

1.单侧检验

若P值＞a，不拒绝H0

若P值＜a，拒绝H0

2.双侧检验

若P值＞，不拒绝H0

若P值＜，拒绝H0

（二）临界值规则

假设检验中，还有另外一种做出结论的方法：根据所提出的显著性水平标准（它是概率密度曲线的尾部面积）查表得到相应的检验统计量的数值，称作临界值，直接用检验统计量的观测值与临界值作比较，观测值落在临界值所划定的尾部（称之为拒绝域）内，便拒绝原假设；观测值落在临界值所划定的尾部之外（称之为不能拒绝域）的范围内，则认为拒绝原假设的证据不足。这种做出检验结论的方法，我们称之为临界值规则。

临界值的双侧检验和单侧检验（图5-6）

图5-6　临界值的检验（双侧与单侧）

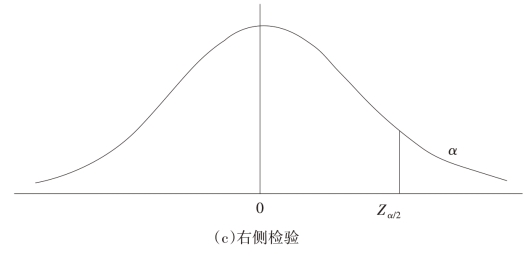
续图5-6 临界值的检验（双侧与单侧）

显然，P值规则和临界值规则是等价的。在做检验的时候，只用其中一个规则即可。

P值规则较之临界值规则具有更明显的优点。这主要是：第一，它更加简捷；第二，在P值规则的检验结论中，对于犯第一类错误的概率的表述更加精确。推荐使用P值规则。最后在得出结论时要注意，在假设检验中，相对而言，当原假设被拒绝时，我们能够以较大的把握肯定备择假设的成立。而当原假设未被拒绝时，我们并不能认为原假设确实成立。

【例5-1】引例中某品牌的咖啡厂商声称其生产的袋装咖啡每袋的平均质量是150克。现从市场上抽取简单随机样本n=100袋，测得其平均质量为149.8 g，样本标准差s=0.872 g。试问该厂商的装袋咖啡质量的期望值否是真如厂商所宣称的是150 g？

解：

H0:μ=150；H1:μ≠150。

由于咖啡的分袋包装生产线的装袋质量服从正态分布，所以其简单随机样本的均值也服从正态分布。我们把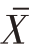标准化成为标准正态变量

根据样本数据计算

P值规则检验

假定a=0.05，根据前面的结果，计算该问题的P值，并做出判断。

解：查标准正态概率表，当z=2.29时，阴影面积为0.9890，尾部面积为1-0.9890=0.011，由对称性可知，当z=-2.29时，左侧面积为0.011。0.011≤a/2=0.025。

0.011这个数字意味着，假若我们反复抽取n=100的样本，在100个样本中仅有可能出现一个使检验统计量等于或小于-2.29的样本。该事件发生的概率小于给定的显著性水平，所以，可以判断μ=150的假定是错误的，也就是说，根据观测的样本，有理由表明总体的m与150 g的差异是显著存在的。

临界值检验

假定a=0.05，根据例6-1的结果，用临界值规则做出判断。

解：查表得到，临界值z0.025=-1.96。由于z=-2.29＜-1.96，即，检验统计量的观测值落在临界值所划定的左侧（即落在拒绝域），因而拒绝μ=150 g的原假设。上面的检验结果意味着，由样本数据得到的观测值的差异提醒我们：装袋生产线的生产过程已经偏离了控制状态，正在向装袋质量低于技术标准的状态倾斜。

这就是说，在假设检验中，相对而言，当原假设被拒绝时，我们能够以较大的把握肯定备择假设的成立。而当原假设未被拒绝时，我们并不能认为原假设确实成立。