所谓参数估计,就是用样本统计量去估计总体的未知参数(或参数的函数)。例如,估计总体均值,估计总体比例和总体方差等等。
参数估计有两种基本形式:点估计和区间估计。下面分别介绍点估计与区间估计的有关概念。前者是用一个数值作为未知参数q的估计值;后者则是给出具体的上限和下限,把q包括在这个区间内。下面分别介绍点估计与区间估计的有关概念。
(一)点估计
1.点估计的分类
点估计主要有矩估计法和最大似然估计法。
矩估计法是用样本矩去估计总体矩(或是用样本矩的函数去估计总体矩的相应函数)的一种估计方法,由此获得的估计量称作矩估计量;最大似然估计法是把待估计的总体参数看作一个可以取不同数值的变量,计算当总体参数取上述不同数值的时候,发生我们当前所得到的样本观测值的不同概率,总体参数取哪一个数值的时候这种概率最大,便把这个数值作为对总体参数的估计结果。
2.估计量的优良标准
前面,我们介绍了总体参数的两种常见的点估计方法,即矩估计法和最大似然估计法。对于同一参数,用不同的方法来估计,可能得到不同的估计量。但究竟采用哪种方法为好呢?这就涉及用什么标准来评价估计量的问题。
判别点估计优良性包括四条标准:无偏性、有效性、一致性和充分性。其中,充分性要求估计量包含了样本中关于θ的全部信息。
无偏性:估计量抽样分布的数学期望等于被估计的总体参数E( )=θ
)=θ
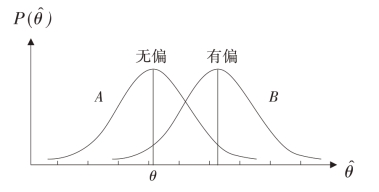
有效性:又称最小方差性。对同一总体参数的两个无偏点估计量,有更小标准差的估计量更有效。
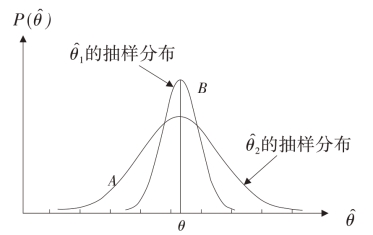
一致性:随着样本量的增大,估计量的值越来越接近被估计的总体参数。![]()

(二)区间估计
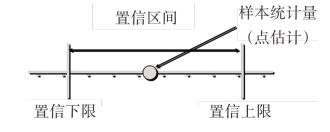
所谓区间估计,实质上就是用两个互相联系的样本统计量给出θ的区间。即以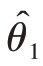 和
和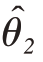 分别作为总体参数θ区间估计的下限与上限,同时要求该区间将θ包含在内的概率应达到一定的程度。即:
分别作为总体参数θ区间估计的下限与上限,同时要求该区间将θ包含在内的概率应达到一定的程度。即:
![]()
式中被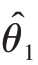 和
和 框定的区间叫作置信区间。
框定的区间叫作置信区间。![]() 叫作抽样极限误差,它可以反映抽样估计误差的最大范围。
叫作抽样极限误差,它可以反映抽样估计误差的最大范围。
置信水平(置信度或置信系数):将构造置信区间的步骤重复多次,置信区间中包含总体参数真实值的次数所占的比例称为置信水平。置信水平通常用1-α来表示,常用的取值是90%,95%,99%。
当样本量给定时,置信区间的宽度随着置信水平的增大而增大,从直觉上说,区间比较宽时,才会使这一区间有更大的可能包含总体参数的真实值。当置信水平固定时,置信区间的宽度随着样本量的增大而减小,换言之,较大的样本所提供的有关总体的信息要比较小的样本多。
因此,作为参数的区间估计,应满足以下两个要求:一是精度性;二是可靠性。
所谓精度性就是估计误差必须控制在一定的范围内。允许误差的最大值,可通过极限误差来反映。显然,Δ越小,估计的精度性越高;Δ越大,估计的精度性越低。极限误差的大小要根据研究对象的变异程度和分析任务的性质来确定。
所谓可靠性是指估计结果正确的概率保证,可用置信度来反映。在区间估计中,置信度十分重要。只有精度而没有置信度的估计是毫无意义的。能够给出置信度的前提条件是,能够证实估计量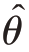 服从(精确地或是近似地)某种已知的常见分布。
服从(精确地或是近似地)某种已知的常见分布。
1.总体均值的估计
设随机变量X~N(μ,σ2),X1,X2,…,Xn是取自X的简单随机样本。根据简单随机样本的定义,自然有各个Xi(i=1,2,…,n)独立,并且与X有相同的分布,即xi~N( μ,σ2)。现在我们来估计X的均值μ。
(1)点估计

(2)区间估计
根据《抽样分布》一节的论述,我们已知![]() 为了进行区间估计,首先,把
为了进行区间估计,首先,把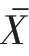 标准化:
标准化:

显然,Z是标准正态变量(见图4-1)。如果我们在图4-1的两个尾部各取面积![]() ,临界值(我们把截取尾部面积的横坐标点叫作临界值)分别为
,临界值(我们把截取尾部面积的横坐标点叫作临界值)分别为 和
和 ,那么,显然有:
,那么,显然有:


图4-1 标准正态分布的双侧临界值
通常,我们先给出置信度1-a的具体数值,根据这个数值查标准正态分布表求得值 ,然后计算置信区间的上、下限。
,然后计算置信区间的上、下限。
(3)总体方差σ2已知的情形
放回抽样的场合:
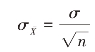
总体均值的置信度为1-α的区间估计为
抽样极限误差为:

不放回抽样的场合:

总体均值的置信度为1-α的区间估计为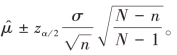
抽样极限误差为:

【例4-8】某企业加工的产品直径X是一随机变量,且服从方差为0.0025的正态分布。从某日生产的大量产品中随机抽取6个,测得平均直径为16 cm,试在0.95的置信度下,求该产品直径的均值置信区间。
解:本例产品数量很多,即总体单位数N很大,故采用放回抽样的有关公式计算。(https://www.xing528.com)
样本平均数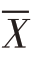 =16
=16
样本平均的标准差![]()
抽样极限误差![]()
所求μ的置信区间为:16-0.04<μ<16+0.04,即(15.96,16.04)。
(4)总体方差σ2未知的情形(大样本)
正态总体或非正态总体、大样本,方差未知时,由于总体方差σ2未知,因此,需要用总体方差的无偏估计量S2来代替总体方差σ2,此时样本均值的抽样分布服从![]() 同理可得,在给定的置信水平1-α下,总体均值μ的置信区间为
同理可得,在给定的置信水平1-α下,总体均值μ的置信区间为
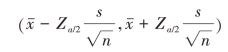
(5)总体方差σ2未知(小样本)的情形
正态总体、小样本,方差未知时,按照与总体方差已知场合相类似的方法,对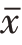 进行标准变换后得到:
进行标准变换后得到:
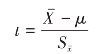
数学上可以证明,当总体为正态分布时,上式服从自由度为n-1的t分布。
在自由度为n-1的t分布的两个尾部各自截取面积 ,查表(或应用Excel工具中的TINV函数),得到各尾部临界值
,查表(或应用Excel工具中的TINV函数),得到各尾部临界值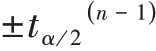 。于是可以写出
。于是可以写出
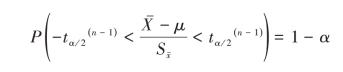
对括号内的不等式作等价变换以后得到
![]()
放回抽样的场合,总体均值的置信度为1-α的区间估计为:

不放回抽样的场合,总体均值的置信度为1-α的区间估计为:
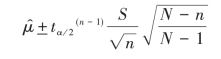
【例4-9】在例4-8中,若总体方差未知,但通过抽取的6个样本测得的样本方差为0.0025,试在0.95的置信度下,求该产品直径的均值置信区间。
解:
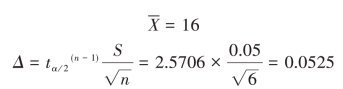
所求μ的置信区间为:16-0.0525<μ<16+0.0525,即(15.95,16.05)。
2.总体比率的估计
(1)点估计
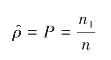
(2)区间估计
由于总体的分布是(0,1)分布,只有在大样本的情况下,才服从正态分布。总体比例可以看成是一种特殊的平均数,类似于总体均值的区间估计,总体比例的区间估计是:
![]()
式中的样本比例标准差在放回抽样条件下是:
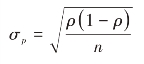
在不放回抽样的条件下是:
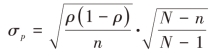
【例4-10】在某市区随机调查了300个居民户,其中6户拥有等离子电视机。试求该区(按户计算的)等离子电视机拥有率的0.95置信区间。
解:本例总体单位数N很大,故采用放回抽样的有关公式计算。
n=300,p=0.02,np=6≥5,可以认为户数n充分大,α=0.05,zα/2=1.96。

因此,所求电视机拥有率的置信区间为0.02-0.0158<r<0.02+0.0158,即(0.0042,0.0358)
3.总体方差的估计
(1)点估计
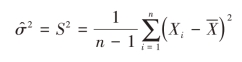
(2)区间估计
根据上一节的论述,我们已知

经推导总体方差的置信度的置信区间为

【例4-11】某公司生产一种健康食品,对每罐食品的质量有一定规定,不允许有过大的差异。设每罐食品的质量服从正态分布。现从生产线上抽查了10个样本,求得其样本方差为9.2,试对总体方差进行置信度为0.90的区间估计。
解: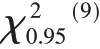 =3.33
=3.33  =16.92
=16.92
置信度为0.90的置信区间为:
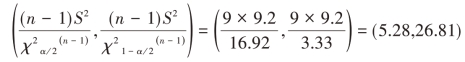
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




