统计学原理：大数定理、正态分布再生和中心极限定理

（一）大数定律

我们通过实例看到随机事件发生的频率在一个常数左右摆动，并且当试验的次数越来越多时，摆动的幅度就越来越小。我们还把这个常数定义为该随机事件发生的概率。但是，我们并没有从理论上证明当试验次数趋于无穷大时，随机事件发生的频率将会趋近于随机事件发生的概率。在本节，我们就来进一步探讨这一问题。

设随机变量序列X1，X2，…，Xn，…相互独立（即任意给定n＞1，X1，X2，…，Xn相互独立），且具有相同的（数学）期望和方差：

E（Xk）=μ，var（Xk）=σ2，k=1，2，…

那么，对于任意给定的ε＞0，有

大数定律表明：尽管个别现象受偶然因素影响，有各自不同的表现。但是，对总体的大量观察后进行平均，就能使偶然因素的影响相互抵消，消除由个别偶然因素引起的极端性影响，从而使总体平均数稳定下来，反映出事物变化的一般规律。

从大数定律来看，我们可以说，大量的独立随机因素对总体的影响当进行平均后在总体均值这里稳定下来，它反映了随机因素综合作用的结果，这就是大数定律的意义。

（二）正态分布的再生定理

如果变量X服从正态分布，总体的平均数是μ，标准差是σ，从这个总体中抽出一个容量是n的样本，则样本平均数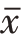也服从正态分布，其平均数E（）仍为μ，其标准差为σ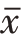。从正态分布的再生定理可以看出，只要总体变量服从正态分布，则从中抽取的样本，不管n是多少，样本平均数都服从正态分布。但是在客观实际中，总体并非都是正态分布。对于从非正态分布的总体中抽取的样本平均数的分布问题，需要由中心极限定理来解决。(www.xing528.com)

（三）中心极限定理

由概率统计我们知道相互独立的多个正态随机变量的线性组合仍然服从正态分布，这就是所谓的正态分布再生定理。由此可知，如果随机变量X1，X2，…，Xn相互独立，且服从同一正态分布N（μ，σ2），那么它们的平均数（均值）就服从正态分布N（μ，σ2/n）。现在的问题是，在实际问题中随机变量不见得都服从正态分布。如果随机变量X1，X2，…，Xn不服从正态分布，情况会是怎样呢？对此，我们有如下极其重要的定理。

1.样本平均数的中心极限定理

如果变量X的分布具有期望值μ和标准差σ，从这个总体抽取容量为n的样本，则当n趋于无穷大时，样本平均数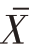近似服从正态分布，其平均数E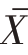（）仍为μ，其标准差为σ。

中心极限定理告诉我们无论总体服从何种分布，只要它的平均数与标准差客观存在，我们就可以通过增大样本容量n的方式，保证样本平均数近似服从正态分布。样本容量n越大，样本平均数的分布就越接近正态分布。

x的分布趋于正态分布的过程如下：

2.样本比例的中心极限定理

从任一总体比例为ρ、方差为ρ（1-ρ）的（0，1）分布总体中，抽取容量为n的样本，其样本比例P的分布会随着n的增大而趋近于平均数为ρ、标准差为σp的正态分布。