抽样类型有概率抽样和非概率抽样,其中非概率抽样是指采用非随机的方法从总体中抽选单元;概率抽样是指基于随机的原则从总体中抽取单元。
【例4-1】有10个同样的球,分别标有从1至10的号码。(1)从中有目的地抽出5号球;(2)从中随便地取一个球;(3)把10个球放在袋中,充分混匀,从中抽出一个球,抽取时,要求袋中各个球有相等的被抽中的概率。
解:显然,(1)和(2)的抽取行为都不是随机试验,因而不属于概率抽样。只有(3)的抽取行为是随机试验。总体的分布可用表4-1的分布列来描述,而(3)的随机试验中所观测的随机变量也有与表4-1有相同的分布。所以,(3)的抽取行为是概率抽样。
表4-1 10个球号码的分布

(一)非概率抽样
非概率抽样的优点是快速简便;费用相对比较低;不需要任何抽样框;对探索性研究和调查设计的开发很有用。缺点是不能对总体进行推断;由于不知总体单元的入样概率,故不能计算估计值的抽样误差。
非概率抽样的具体方法有随意抽样、志愿者抽样、判断抽样、配额抽样和滚雪球抽样。
1.随意抽样
样本单元的抽选以随意的方式进行。如街道拦截访问。
2.志愿者抽样
被调查者都是自愿参与调查。如网上问卷,自愿回答。
3.判断抽样
由专家有目的地挑选“有代表性”的样本进行调查。如典型调查。
4.配额抽样
从总体的各个子总体中选取特定数量的样本单元组成样本。如市场调查中,规定男女消费者的样本各多少。
5.滚雪球抽样
适合于总体中某种较为稀少的特殊子总体而又缺少完整的抽样框。抽样时通过已知的少数个体获得信息逐渐扩大。
(二)概率抽样
概率抽样是从总体中随机抽选样本单元,被抽中的单元既不取决于调查人员的愿望,也不取决于被调查者的态度;每一个单元都有一定的概率被抽中。它的优点是可以对总体进行推断,并能计算估计值的抽样误差;缺点是相对于非概率抽样,设计比较复杂,而且费用也比较高。
常见的概率抽样方法主要有简单随机抽样、系统抽样、整群抽样、分层抽样(STR)、多阶抽样以及多相抽样等。
1.简单随机抽样
(1)定义
简单随机抽样是从总体的N个抽样单元中,每次抽取一个单元时,使每一个单元都有相等的概率被抽中,连续抽n次,以抽中的n个单元组成简单随机样本。
(2)优点
①比较容易理解和掌握;
②抽样框不需要其他辅助信息;
③理论上比较成熟,有现成的方差估计公式。
(3)缺点
①没有利用辅助信息;
②样本分散,面访费用较高;
③有可能抽到较差的样本;
④抽选大样本比较费时。
当所研究的总体为有限总体时,简单随机抽样又分为放回抽样和不放回抽样:
①放回抽样
放回抽样的具体做法是:从总体中抽出一个样本单位,记录其标志值后,又将其放回总体中继续参加下一轮单位的抽取。放回抽样的特点是:第一,n个单位的样本是由n次试验的结果构成的。第二,每次试验是独立的,即其试验的结果与前次、后次的结果无关。第三,每次试验是在相同条件下进行的,每个单位在多次试验中选中的机会(概率)是相同的。在放回抽样中,样本可能的个数是Nn,N为总体单位数,n为样本容量。
②不放回抽样
不放回抽样是指从总体抽出一个单位,登记后不放回原总体,即不参加下一轮抽样,下一次继续从总体余下的单位中抽取样本。其特点是:第一,包含n个样本单位的样本是由n次试验的结果构成,但由于每次抽取后不放回,所以实质上相当于从总体中同时抽取n个样本单位。第二,每次试验结果不是独立的,上次中选情况影响下一次抽选结果。第三,每个单位在多次试验中选中的概率是不等的。在不放回抽样中,如果考虑顺序,其样本可能数为![]() ;如果不考虑顺序,其样本可能数为
;如果不考虑顺序,其样本可能数为![]()
2.系统抽样
(1)定义
系统抽样又称等距抽样,对研究的总体按一定的顺序排列,并按某种规则确定一个随机起点,然后每隔一定的间隔抽取一个单位,直到抽取n个单位形成一个样本。
(2)抽选方法
设总体单元数为N,要抽n个单元为样本,先计算抽样间隔k=N/n,在1到k之间抽取一个随机起点r,则被抽中单元的顺序位置是:r,r+k,r+2k,…。

(3)优点(https://www.xing528.com)
等距抽样方式相对于简单随机抽样方式最主要的优势就是经济性。等距抽样方式比简单随机抽样更为简单,花的时间更少,并且花费也少。
(4)缺点
使用等距抽样方式最大的缺陷在于总体单位的排列上。一些总体单位数可能包含隐蔽的形态或者是“不合格样本”,调查者可能疏忽,把它们抽选为样本。
3.整群抽样
(1)定义
调查时先将总体划分成若干群,然后抽样时以群为抽样单位从中抽取部分群,进而对抽中的各个群中所包含的所有单位进行调查或观察的抽样方法就称为整群抽样。
整群抽样的示意图:

(2)优点
①能大大降低收集数据的费用;
②当总体单元自然形成的群时,容易取得抽样框,抽样也更容易;
③当群内单元差异大,而不同群之间的差异小时,可以提高效率。
(3)缺点
①若群内各单元有趋同性,效率将会降低;
②通常无法预先知道总样本量,因为不知道群内有多少单元;
④方差估计比简单随机抽样更为复杂。
4.分层抽样
(1)定义
在抽样之前将总体分为同质的、互不重叠的若干子总体,这些子总体也称为层。然后从每一个层中独立地随机抽取一定数量的单位组成一个样本的抽样方式即为分层抽样。在分层时,应使层内各单位的差异尽可能小,而使层与层之间的差异尽可能大。
分层抽样示意图:
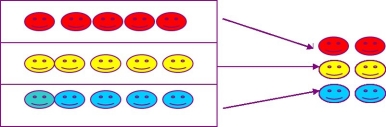
(2)优点
①由于性质相同的单元分在同一层,层内差异缩小,可以提高抽样效率;
②可以得到各层子总体的估计;
③操作与管理方便;
④能避免得到一个“差”的样本。
(3)缺点
①对抽样框的要求比较高,必须有分层的辅助信息;
②收集或编制抽样框的费用比较高;
③若调查变量与分层的变量不相关,效率可能降低;
④估计值的计算比简单随机抽样复杂。
5.多阶抽样
(1)定义
先将总体划分为R个群,从群中随机抽取r个群,再从r个群中随机抽取m个子群构成下一级抽样单位,以此类推,最后抽取其中范围更小的单元作为调查单位。
多阶抽样示意图:

(2)优点
①当群具有同质性时,多阶抽样的效率高于整群抽样;
②样本的分布比简单随机抽样集中,采用面访可以节约时间和费用;
③不需要整个总体单元的名录框,只要群的名录框和抽中群的单元名录框。
(3)缺点
①效率不如简单随机抽样;
②通常不能提前知道最终的样本量;
③调查的组织较整群抽样复杂;
④估计值与抽样方差的计算较为复杂。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




