统计学原理：中位数与众数的比较

（一）中位数

将总体中各单位的标志值按大小顺序加以排列，处在数列中间位置的标志值就是中位数。若总体单位数是奇数，中间位置的标志值是中位数；若总体单位数是偶数，则居中间的两个标志值的算术平均数是中位数。

中位数的确定方法依据掌握的资料不同而有所区别。对于未分组的资料，只需将各变量值按大小顺序排列，根据变量值的个数确定中位数所在位次，即中位数的位置=（其中：n代表变量值的个数）；对于单项式变量数列，其中位数的确定方法是累计次数（向上累计或向下累计）的一半，找出中位数组的数值即可；对于组距式变量数列，确定中位数所在组的方法与单项式变量数列相同，然后一般通过下列公式计算确定中位数：

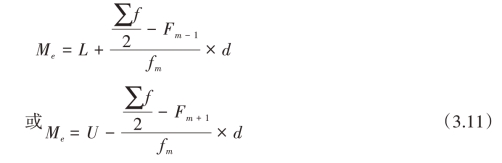
其中：Me代表中位数；∑f是总体单位总数；L为中位数所在组的下限；U表示中位数所在组的上限；fm是中位数所在组的次数；Fm-1为中位数所在组的前一组的累计次数（向上累计）；Fm+1为中位数所在组的后一组的累计次数（向下累计）；d为中位数所在组的组距。

例如，某公司30名工人劳动生产率（千克／时）资料如表3-7所示：

表3-7　某公司30名工人劳动生产率（千克／时）资料

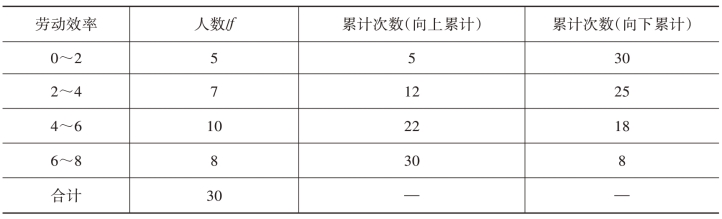
根据，可以看出中位数所在组为第三组。则中位数的计算如下：

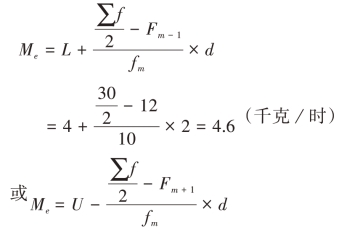
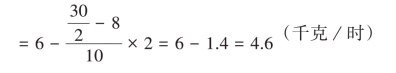
通过上述计算可以发现：中位数的确定仅取决于它在数列中的位置，所以不受极端数值的影响，在这一点上它优于算术平均数。因此，在某些经济现象中，用它来表示现象的一般水平比算术平均数更具有代表性。

（二）众数

众数是指分配数列中出现次数最多的标志值。它是总体中最常遇到的变量值，是最普遍、最一般的，因而，可以用来说明社会现象的一般水平。

众数的确定比较简单，对于未分组资料和单项式变量数列，只需直接观察找出次数最多的变量值即为众数；对于组距式变量数列，首先找出次数最多的组，即众数组，然后一般通过下列公式计算确定众数：

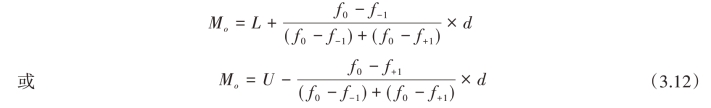
其中：Mo为众数；L为众数组的下限；U为众数组上限；f-1为众数组前一组的次数；f0为众数组的次数；f+1为众数组后一组的次数；d为众数组的组距。(www.xing528.com)

根据表3-7的资料，我们不难发现，出现次数最多的是第三组，即众数组4～6那一组。则众数计算如下：

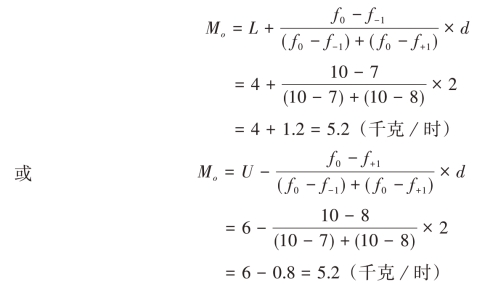
众数和中位数一样，也是一种位置平均数，它不受极端值的影响，在组距数列中出现开口组时，对众数也没有影响，只是当各标志值皆不相同或各标志值出现次数一致时，就不存在众数。

（三）四分位数、十分位数和百分位数

四分位数是将数据由小到大排序后，位于全部数据1/4位置上的数值。

十分位数是将数据由小到大排序后，位于全部数据1/10位置上的数值。

百分位数是将数据由小到大排序后，位于全部数据1/100位置上的数值。中位数也就是第二个四分位数、第五个十分位数、第五十个百分位数。

分位数与其他指标结合，可以更详细地反映数据的分布特征。

（四）众数、中位数和算术平均数的比较

1.算术平均数综合反映了全部数据的信息，众数和中位数由数据分布的特定位置所确定。

2.算术平均数和中位数在任何一组数据中都存在而且具有唯一性，但计算和应用众数有两个前提条件：数据项数众多；数据具有明显的集中趋势。

3.算术平均数只能用于定量（数值型）数据，中位数适用于定序数据和定量数据，众数适用于所有形式（类型、计量层次）的数据。

4.算术平均数要受数据中极端值的影响，而众数和中位数都不受极端值的影响。

为了排除极端值的干扰，可计算切尾均值，即去掉数据中最大和最小的若干项数值后计算的均值。

切尾均值是将均值与中位数取长补短的结果。

5.算术平均数可以推算总体的有关总量指标，而中位数和众数则不宜用作此类推算。

皮尔逊经验公式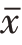：（-Mo）≈3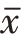（-Me）