数值平均数：几何平均数—统计学原理

几何平均数（G）是分配数列中n个单位标志值连乘积的n次方根。它适合于计算现象的平均比率或平均速度，反映现象增长率的平均水平。

几何平均数按掌握的资料不同，分为简单几何平均数和加权几何平均数两种。

（一）简单几何平均数

简单几何平均数适用于计算未分组变量值的平均比率或平均速度。

其计算公式为：

其中：G代表几何平均数；x代表各个变量值；n表示变量值的个数；∏代表连乘符号。

例如，某机械厂生产机器，设有毛坯、粗加工、精加工、装配四个连续作业的车间，本月份毛坯车间制品合格率为97%，粗加工车间制品合格率为93%，精加工车间制品合格率为91%，装配车间制品合格率为87%，在确定车间平均合格率时，由于后续车间的合格率是在前一车间制品全部合格的基础上计算的，全厂产品的总合格率并不等于各车间制品合格率之和，而是等于各车间制品合格率的连乘积。所以，不能采用算术平均数和调和平均数，必须利用几何平均数来计算，即：

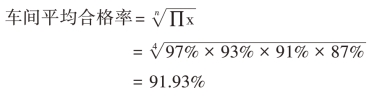
在标志值数量较多的情况下，计算几何平均数需开高次方，为了计算上的方便，可以用对数简化计算，对几何平均数计算公式的两边同时取对数，则有：

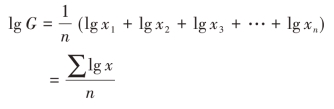
可见，几何平均数的对数，实质上是各个变量值的对数的算术平均数。求出了几何平均数的对数之后，再由反对数找出真数，即为几何平均数。

在上例中，按对数方法计算车间平均合格率为：

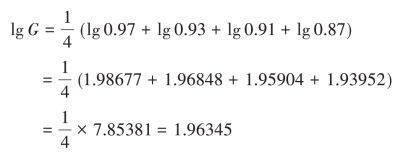
求反对数得车间产品合格率为91.93%。

（二）加权几何平均数(www.xing528.com)

加权几何平均数适用于计算分组数列的平均比率或平均速度。

其计算公式为：

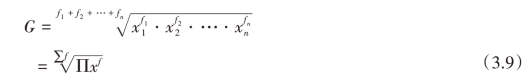
其中：f为变量值的次；∑f表示次数总和；x代表各组变量值；∏为连乘符号。

为了计算上的方便，对上述公式两边同时取对数，得：

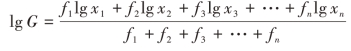
由此可见，加权几何平均数的对数，实质上是各变量值对数的加权平均数。求出几何平均数的对数后，再由反对数找到真数，即为几何平均数。

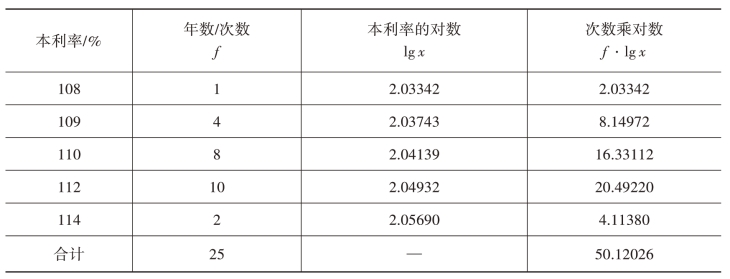
例如，建设银行某项投资的年利率是按复利计算的，25年的年利率分配是：有1年为8%，有4年为9%，有8年为10%，有10年为12%，有2年为14%。在确定平均年利率时，由于按复利计息，各年的利息是在前年的累计存款额（本金加利息）的基础上计息，所以，应先将各年的利率换算成各年本利率（1+年利率）。这时，总的本利率就等于各年本利率的连乘积，可以用加权几何平均数公式计算出年平均本利率，然后用年平均本利率扣除100%，即可得到平均年利率。计算过程如表3-6所示。

表3-6　平均本利率计算过程表

则按对数方法计算年平均本利率为：

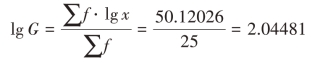
求反对数得年平均本利率是G=110.87%

平均年利率=110.87%-100%=10.87%

由此可见，凡是现象的变量值的连乘积等于总比率或总速度，都可以使用几何平均数来计算其平均比率或平均速度。