数值平均数的计算方法及意义

算术平均数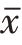（）是统计中最基本也是最常用的一种平均数。它是用分布数列中总体各单位标志值的总和除以全部单位数而得到的比值。其基本计算公式为：

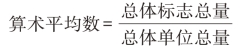
在实际应用中，由于所掌握的资料不同，算术平均数可分为简单算术平均数和加权算术平均数两种。

（一）简单算术平均数

它是直接将总体各单位的标志值相加之和除以总体单位的个数而得到的平均数。其计算公式为：

其中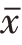：代表算术平均数；x代表各单位标志值；∑是总和符号；n代表总体单位个数。

例如，某工厂生产班组有5个工人，日产零件数分别为21件、23件、25件、27件和29件，则平均每人日产零件数为：

可见，简单算术平均数适用于资料未分组的情况下。

（二）加权算术平均数

为了体现各变量值轻重不同的影响作用，对各个变量值赋予不尽相同的权数（fi）。

当各变量值出现的次数不同，也就是资料已经分组形成变量数列的情况下，平均数的计算要采用加权算术平均数的形式。其计算公式为：

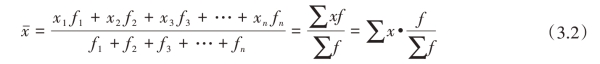
其中，x代表各组的标志值；f代表各组所对应的次数（权数）；表示各组次数占总次数的比重（频率）。

从上述计算公式中我们不难发现：加权算术平均数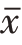（）的大小，不仅取决于各组变量值（x）的大小，而且受各组次数占总次数比重的影响。某组的次数占总次数比重越大，说明该组标志值对平均数的影响程度愈高；反之，某组的次数占总次数的比重越小，说明该组标志值对平均数的影响程度就小。平均数的数值大小总是趋近于次数占总次数比重较大的那一组的标志值。可见，各组次数占总次数比重的大小对平均数的大小起着权衡轻重的作用。当各组次数相等时，也就是各组次数占总次数比重完全相同时，权数（包括绝对数权数f和比重权数对平均数的影响作用也就消失了。这时，加权算术平均数就等于简单算术平均数。即：

当f1=f2=f3=…=fn时

这说明简单算术平均数是加权算术平均数的一种特例。

由于变量数列包括单项式变量数列和组距式变量数列两种，所以，加权算术平均数的计算也分为以下两种情况：

（1）根据单项式数列计算加权算术平均数时，直接用各组标志值与各组次数乘积的总和除以各组次数总和即可。

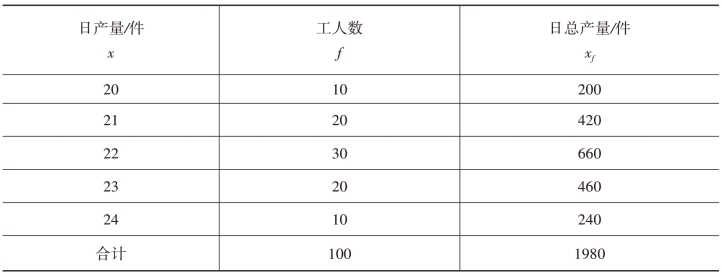
例如，某公司100名工人的日产量如表3-1所示：

表3-1　某公司工人日产量表(www.xing528.com)

则这100名工人的平均日产量为：

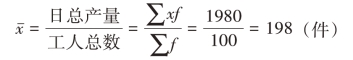
（2）根据组距式变量数列计算加权算术平均数时，首先在一定假定条件（即假定变量值在各组内是均匀分布的）下计算各组的组中值以代表各组的标志值，然后用各组标志值与各组次数乘积的总和除以各组次数总和即可。

例如，某轻工企业60名工人四月份、五月份包装某种产品的数量如表3-2所示：

表3-2　某轻工企业60名工人四月份、五月份包装某种产品的数量表

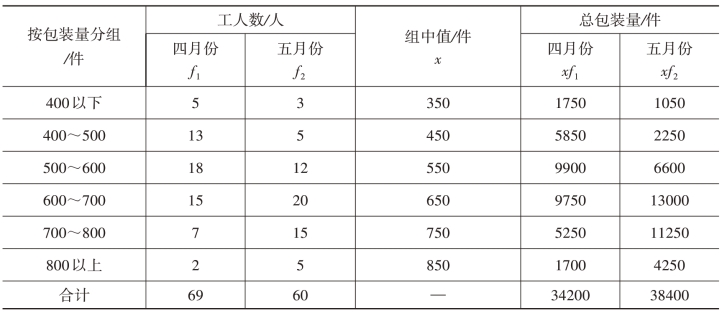
则60名工人平均每人日包装量为：

四月份：

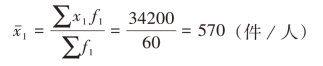
五月份：

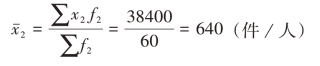
可见，在各组标志值不变的情况下，各组人数占总人数比重的大小，对平均数大小起着决定性的作用。四月份日包装量在600件以下的有36人，占总人数的60%，使得平均包装量低于600件；五月份日包装量在600以上的人有40人，占总人数的67%，导致平均包装量高于600件。

需要说明的是：在计算加权算术平均数时，对于权数（f）的选择必须慎重，务必使各组的标志值和权数的乘积等于各组的标志总量，具有实际的经济意义。

例如，某市某局所属15个企业产值计划完成情况如表3-3所示：

表3-3　某市某局所属15个企业产值计划完成情况

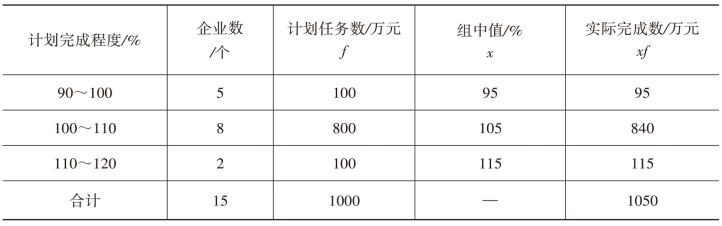
在计算15个企业产值计划平均完成程度时，究竟以企业数为权数还是以计划任务数为权数，是本题的关键。企业数虽然是完成产值计划不同程度的次数，但并不适合作权数。各组的计划完成程度（组中值）与企业数相乘没有实际经济意义，而各企业由于规模大小不同，下达的计划任务数也应有所区别，所以，分析产值计划平均完成程度时，必须联系下达的计划任务数来计算，即以计划任务数为权数；通过实际完成产值数与产值计划任务数对比来确定15个企业平均计划完成程度。计算过程为：

（三）算术平均数的主要数学性质

1.算术平均数与变量值个数的乘积等于各个变量值的总和。

2.各变量值与算术平均数的离差之总和等于零。

3.各变量值与算术平均数的离差平方之总和为最小。