学习统计学原理，图表分析成果

（一）条形图

条形图是用宽度相同的条形的高度或长短来表示数据变动的图形。条形图可以横置或者纵置，纵置时也称为柱形图。条形图有单式、复式等形式。例如，根据表2-3数据绘制的条形图如图2-1所示。

图2-1　某班学生考试成绩条形图

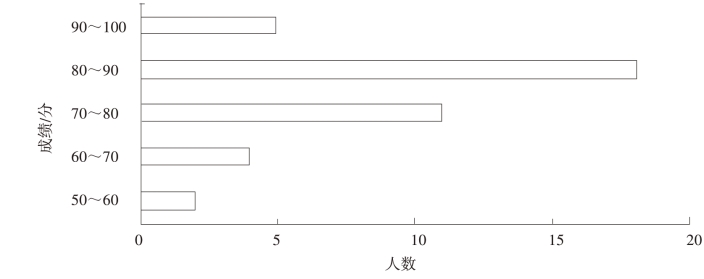
（二）饼图

饼图也称圆形图，是用圆形及圆内扇形的面积来表示数值大小的图形。饼图主要用于表示总体中各组成部分所占的比例，对于研究结构性问题十分有用。在绘制饼图时，总体中各部分所占的百分比用圆内的各个扇形面积来表示。

【例2-3】某年某学院5个专业考研报名人数情况如表2-5所示，用饼图来描述这5个专业的考研报名情况。

表2-5　某年某学院5个专业考研报名人数情况统计表

解：根据表2-5的资料绘制饼图，如图2-2所示。

图2-2　某年某学院5个专业考研报名人数统计图

（三）直方图

直方图是用直方形的宽度和高度来表示次数分布的图形。绘制直方图时，横轴表示各组组限，纵轴表示次数（一般标在左方）和比率（或频率，一般标在右方）。依据各组组距的宽度与次数的高度绘制成直方形。

（四）折线图

折线图是以线段的起伏表示其数量分布的特征，绘图时，可以在直方图的基础上，用折线将各组次数高度的坐标连接而成，也可以用组中值与次数求坐标点连接而成。例如，根据表2-3数据绘制的直方图和折线图分别如图2-3、图2-4所示。

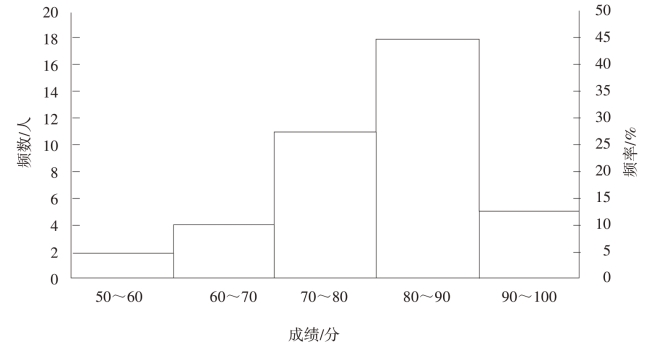
图2-3　某班学生考试成绩直方图

图2-4　某班学生考试成绩折线图

（五）散点图(www.xing528.com)

散点图是以一个变量为横轴，另一个变量为纵轴，利用散点的分布形态反映变量统计关系的一种图形。散点图能直观表现出影响因素、预测现象之间的总体关系趋势，还能反映变量间关系的密切程度。

【例2-4】水稻产量与化肥施用量的一组观测数据如表2-6所示，根据以下数据绘制散点图。

表2-6　化肥施用量与水稻产量相关数据

解：根据表2-6的资料绘制饼图，如图2-5所示。

图2-5　化肥施用量与水稻产量散点图

（六）茎叶图

茎叶图是由“茎”和“叶”两部分构成，其图形是由数字组成的，保留原始资料的信息。通常情况下是将高位数作为茎，而将末位数作为叶。用茎叶图表示数据，一方面可以看出数据分布的形状及数据的离散状况；另一方面茎叶图中的数据可以随时记录、随时添加，方便记录与表示。

（七）箱线图

箱线图是利用一组数据中的五个统计量（最小值、最大值、下四分位数、中位数、上四分位数与最大值）来描述数据的一种方法，主要用于反映原始数据的分布特征，还可以进行多组数据分布特征的比较。通过箱线图可以看出数据是否具有对称性、分布的分散程度等信息。

（八）线图

线图是在平面坐标上用折线表现数量变化特征和规律的统计图。线图主要用于显示时间序列数据，以反映事物发展变化的规律与趋势。

（九）累计曲线图

1.累计曲线图的绘制

累计频数（频率）分布图分为向上累计频数（频率）分布图和向下累计频数（频率）分布图。不论是向上累计还是向下累计，均以分组变量为横轴，以频数（频率）为纵轴。在直角坐标系上将各组组距的上限与其相应的累计频数（频率）构成坐标点，依次用折线（或光滑曲线）相连，即得到向上累计曲线图。在直角坐标系上将各组组距的下限与其相应的累计频数（频率）构成坐标点，依次用折线（或光滑曲线）相连，即得到向下累计曲线图。

2.洛伦茨曲线图

洛伦茨博士（Dr.M.O.Lorenz）把累计频数（频率）分布曲线运用于研究社会财富、土地和工资收入的分配是否公平，这种累计曲线又称洛伦茨曲线图。

3.基尼系数

统计学家基尼（Gini）在洛伦茨曲线图的基础上进一步提出了一个衡量收入分配公平程度的指标——基尼系数。