欧几里得生活于希腊化时代早期,与他大致同时代的还有两位空前绝后的大数学家,阿基米得和阿波罗尼奥斯。
阿基米得除了在力学上的工作之外,在数学上也有许多成就,如他创造大数计法描述非常庞大的数,计算椭球体和抛物线体的体积,用穷竭法把π精确到3.14等,他还使用了某些堪称微积分先驱的方法。但阿基米德的著作在古代世界影响较小,其抄本非常偶然地被保存下来,到文艺复兴时期才重新受到重视。还有一部重要的作品直到1906年才重见天日,它曾经被抄写在一卷羊皮书上,然后被擦除,重新抄写了一本祈祷书,20世纪的学者重新复原了其中幸亏并未被擦干净的字迹,复原出的作品中包含了两篇早已失传的文章。
阿波罗尼奥斯是本轮—均轮模型的创造者,他的《圆锥曲线论》更是影响巨大,他同时为托勒密和开普勒提供了数学模型。
他还有许多著作已经佚失了。《几何原本》和《圆锥曲线论》反映了希腊时期几何学的最高成就,以至于它们之前的许多著作都失传了。
阿波罗尼奥斯达到了解析几何之前研究圆锥曲线的最高成就,在某种意义上他是解析几何的先驱,但实质上还相差甚远,他在研究圆锥曲线时经常使用某些参照线,它们的功能有些类似于坐标轴,但这些参照线更多地仍然是根据具体情况在图形上作出的辅助线,而不是先于具体图形就被设立的坐标系。
阿波罗尼奥斯到托勒密之间,在三角学方面有许多发展,我们略过不讲,重点讲希腊化晚期的丢番图(约公元246年—330年)。
丢番图被称作代数学之父,他与传统的希腊数学风格迥异,不再基于几何学,而是用一系列缩写形式来描述方程与不定方程。
他也开始处理高次幂,4次方被称作平方平方,5次方是平方立方,都有某些缩写的表达方式。比如2x4+3x3-4x2+5x-6这个式子可以表达为形如:
SS2 C3 x5 M S4 u6(https://www.xing528.com)
这样的形式,其中S、C、x、M和u分别代表平方、立方、未知数、减和单元。[4]这里是用拉丁字母替换了丢番图的记号,他自己的写法看起来是下面这样:
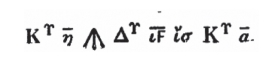
图11.5.1 丢番图符号
相当于x3·8-x2·16=x3。
但丢番图没有把他的研究定位于某种一般性的代数法则的研究,他的著作更多地是一部难题集,回答的都是有明确实例的问题,在方程有多个解时,往往只取其中的一个,甚至对那些无穷多解的不定方程,往往也只给出一个解就完了,当然负根和无理数都不被接受。
丢番图在古代数学史中显得独树一帜,当然这也可能是因为在他之前之后的数学著作都失传了。在中世纪,丢番图影响不大,代数学的渊源主要来自阿拉伯数学家花拉子米,但到了文艺复兴时期,韦达重新阐释了丢番图的著作(图11.5.2),推动了现代的符号代数的兴起。

图11.5.2 丢番图著作的拉丁文译本(1621年)
我在讲阿拉伯科学的时候提过了花拉子米,在某些方面花拉子米要比丢番图“落后”,他没有采用任何缩写形式,甚至连他本人引进的印度数字都很少使用,全文都是大量的文字叙述。他的代数方法也是基于几何学的,但如果翻译成现代符号的话,我们将发现他关注的问题更接近于现代的代数学。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




