我们说过,这些概念的梳理很大部分是由中世纪经院学者完成的,然而即便到了伽利略那里,亚里士多德的思维惯性仍然在发挥作用,例如伽利略仍然没有完全放弃自然运动和受迫运动的区分,他认为自由落体运动是自然运动。
提到伽利略,我们经常想到传说中的比萨斜塔落体实验,据说伽利略在比萨斜塔顶部让两个球同时下落,发现更重的球和更轻的球同时落地,从而反驳了亚里士多德物理学所认为的重球落得更快的说法。
我们不知道伽利略本人是否真的在比萨斜塔上做过实验,不过他的确应该做过类似的实验[1],这个实验本身不是最关键的,事实上稍早之前的斯台文(公元1548年—1620年)也做过类似实验,甚至在公元6世纪就有拜占庭学者做过。
这些实验的确显示了重球和轻球差不多同时落地,但这充其量只能说是对亚里士多德物理学的一种挑战,远远不能否定整个亚里士多德物理学。我们会说在许多情况下之所以观察到重物落地更快,是由于空气阻力,但亚里士多德也可以说,我们之所以观察到重球和轻球落得差不多快,也是因为空气介质的问题,比如我们可以再做个实验,把两个球放在水中让它们下落,就会发现在体积相同的情况下重球确实比轻球快。而在亚里士多德那里,运动之所以有速度就是为了克服介质的阻力,如果没有介质,物体就应该直接到达目的地,也就是具有无限快的速度,当然亚里士多德否认真空的存在,但我们也可以设想在越稀薄的介质中,运动受到的阻力越可以忽略不计,重物和轻物的速度差异也就会越小。
因此这个落体实验之所以能被认为是对亚里士多德的反驳,也同样需要一系列概念的重新建构,包括对运动和对空间的新理解,包括认识到空气阻力的特性等。当然最关键的是,伽利略不只是定性地反驳了亚里士多德,还给出了落体运动的量化规律,那就是“从静止开始下落的物体在相等时段内经过的距离彼此成从1开始的奇数关系。”[2]
我们提到过,定量计算匀加速运动的中速度定理已经在经院哲学家那里给出了。但经院哲学家只是停留于假设,而没有把他们的理论设想与现实世界结合起来,他们研究的是一种假设中的匀加速运动,并没有考虑它究竟对应于现实世界中的哪种运动,更没有把它与自由落体联系起来。
而伽利略的贡献在于把理论想象和实验研究整合在一起,他基于理论构想来设计实验,对实验结果进行理论阐发。
伽利略不是首先通过大量的实验最后才分析出量化关系的,他一开始就得到了落体运动是匀加速运动的结论,亦即速度与时间呈正比。理由是“自然喜欢简单”,他说道“既然自然已经赋予下落的重物某种特殊的加速……在运作这一切时,她习惯于使用那些最平常、最简单和最容易的手段……没有比永远以同样方式重复进行的增加或增长更为简单的了。”[3]
我们说过伽利略仍然坚持亚里士多德的“自然运动”概念,而他认为自由落体是自然运动,那么既然它是自然的,就应该是以最简单、最经济的方式完成的。它当然不可能是匀速运动,因为初速度为零嘛。那么如果它是加速运动,一定是以最简单的方式加速的,那么就是匀加速运动了[4]。
匀加速运动的中速度定理经院学者已经得到了,伽利略也表示这个大家都知道,所以说问题就是如何验证落体运动恰好就是匀加速运动。伽利略一方面通过对自然的简单性的直觉把握到了这件事,但他的实验更主要的目的是确认并演示这种对自然的把握,而不是指望从实验中直接总结出规律。在某些场合,伽利略甚至表示实验是完全不必要的,他说道“在我看来,没有实验,我也确信结果将会像我告诉您的那样发生,因为它必然会这样发生。”[5]
比起伽利略实际在斜塔上做的落体实验,下面这个思想实验更加重要:假设重球真的比轻球下落得快,那么如果把两个球绑在一起下落,轻球应该会拖重球的“后腿”,结果下落速度应该比单个重球更慢,但从另一个角度看,绑在一起的两个球相当于一个更重的物体,按照更重则下落更快的假设,绑在一起的两个球应该比重球落得更快。于是我们得到了矛盾的结果,证明最初的假设不成立,重球必定和轻球下落得一样快。
的确,当我们做完这一思想实验后,无论有没有再去实地做实验,都已经确信结果“必然会这样发生”。伽利略认为其他许多问题也是类似,如果我们能够在思想中考虑周全,实验就变得可有可无了。(https://www.xing528.com)
伽利略著名的“斜面实验”只是为了确认实际的落体运动就是理论中的匀加速运动,他不认为做这一实验是为了增加某些新知识,更不是为了在实验中归纳出匀加速运动的计算公式。伽利略通过对斜面运动的测量,证明它是匀加速运动,因此就确认了自由落体运动也是匀加速运动。
但为什么小球沿斜面的滚动是匀加速运动,就证明了自由落体也是匀加速运动呢?伽利略是这样考虑的:在斜面运动的研究中,我们发现小球的运动规律与斜面的坡度无关,那么我们就可以设想斜面的极限情形,其中之一就是这个斜面变成完全竖直(图10.2.1),那么此时就是自由落体运动了。当时的技术手段能够测量较平缓的斜面运动的情形,但难以精确测量自由落体运动,而伽利略通过理论推演确信他关于斜面运动的研究可以推广到自由落体运动。

图10.2.1 斜面运动的规律与角度无关
但这里伽利略的推理其实是错误的,因为在任何坡度的斜面上,小球实质上是滚下来的,越落越快的同时还越滚越快,但在自由落体的情形下,小球没有滚动。因此这两种情形下的运动结果肯定是不一样的。事实上伽利略在他所宣称的通过反复实验得到的炮弹自由落体的数据是错误的,这很可能就是因为他实质上没有直接做炮弹实验,而是拿斜面实验的数据去推测了。[6]
所以我们不应过高地估计实验在近代早期科学中的意义,伽利略他们的实验更多的是演示性而非发现性的,但是做实验这件事情本身仍然意义重大,这标志着理论想象和经验研究的统一化,标志着数学世界和现实世界的统一化。所以胡塞尔等哲学家把伽利略认作近代科学“自然的数学化”的标志,这是不无道理的。
斜面运动的极限情况除了完全竖直之外,还有一种是完全水平。伽利略发现小球在下坡的时候越跑越快,在上坡的时候越跑越慢,那么在既不上坡又不下坡的情况下会怎么样呢?他认为,如果没有阻力的话,小球在一个无限的水平面上应该会无限地保持其速度运动下去。
这里伽利略几乎已经得到了牛顿第一定律,也就是惯性定律。不过在这里,伽利略始终还差了一步,或许是因为他想得太多了。伽利略想,这个无限的“水平面”是否可能呢?注意到“水平面”不同于“平面”,只有在尺度非常小的情况下它们才近似等同。我们知道地球是圆的,在某一点沿着一条“直线”走,其实你是在不断上坡的,实际的“水平面”应该是沿着地球表面的弧形面(图10.2.2),所以说伽利略意义上的“惯性”不是维持匀速直线运动的倾向,而是维持围绕地球的圆周运动。
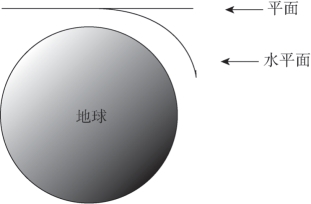
图10.2.2 平面和水平面
伽利略的运动概念仍然在很大程度上是亚里士多德式的,是有方向的,是相对的、有所归宿的,而不是牛顿那样的在一个各向同性的无限空间中的运动。伽利略同意亚里士多德的观点,认为“物体不可能朝着它不可能达到之处运动”[7],因此在宇宙意义上,理想的直线运动亦即朝向无穷远处的运动,是不可能存在的。
所以说牛顿所谓的“绝对空间”观念并不只是简单的画蛇添足,伽利略恰恰因为没有把空间绝对化,认为运动始终是相对于什么的运动,因而没能摆脱亚里士多德的束缚。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




