在珠算流行之前,中国人的计算方式主要是筹算,算筹最初就是竹制的小圆棍(图6.6.1),也许与八卦的长短棍同源。所谓“运筹帷幄之中”就是运的这些小竹棍了。老子就说过“善数者不用筹策”,可见筹算至少在春秋时期就已经流行了。算筹分横式和纵式记法,横式用横置的算筹表示1,竖置的算筹表示5,纵式反之。几组算筹横向排列,以十进制表示数字。筹算有一套四则运算的方式,并逐渐发展出开方、列方程等复杂的算法(图6.6.2)。

图6.6.1 汉代骨制算筹
到晚近时期,算盘取代算筹成为主要的算术工具。无论是算筹还是算盘,与笔算相比,其优点和缺点都是可以抹去中间过程,中国古代的数学始终是重结果、重实用,而不重视过程和证明的。
中国古代的代数方法最初也是由算筹形式表现的,古代中国和古代希腊数学中都没有现代这样以x、y、z、a、b、c等符号表达的简洁的等式,希腊人以几何学的方式做代数问题,而中国人也以某种方式把代数问题空间化。例如汉代的《九章算术》中就用把算筹放在不同方格的形式表达多元一次方程。
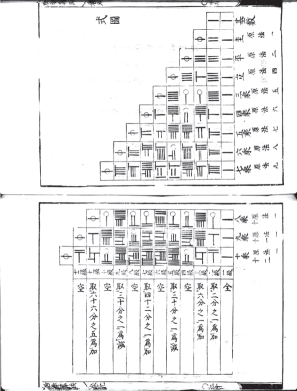
图6.6.2 日本18世纪教科书讲解筹算
在宋代,一套非常精致的代数表达和演算系统被发展出来,那就是“天元术”。天元术以表示常数的“太”出发,最多可以向四个方向延伸,分别为天、地、人、物,延伸的第1格为1次,第2格为2次,以此类推,在相应的格子里放入算筹,负数的话就多加一条斜线。如图6.6.3表示方程2x2+18x-316=0。
天元术在明朝已经逐渐失传,直到清朝在西学东渐的刺激下,才被中国数学家重新发现其价值。相比西方近代的符号化代数,天元术看起来非常优美,但终究还是缺乏灵活性和普遍性。
在几何学方面,中国人虽然不擅长证明,但在测算方面有所特长,魏晋时期刘徽的《九章算术注》创立割圆术,通过圆内接正192边形的面积,得出π≈3.14,南北朝时期的祖冲之(公元429年—500年)父子更是计算到圆内接正6144边形和正12288边形的面积,得出π=3.1415926~3.1415927,领先西方人将近一千年。刘徽还著有《海岛算经》(图6.6.5),用两次或多次测望所得的数据推算海岛的高度和远近。(https://www.xing528.com)
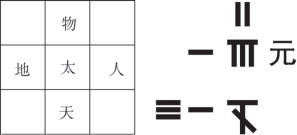
图6.6.3 天元术

图6.6.4 朱世杰在天元术基础上发展出的四元术,可以处理四元高次方程(图中字母是现代方程的表达方式)
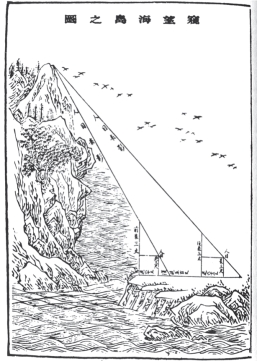
图6.6.5 刘徽《海岛算经》
当然中国人也不是完全不会证明。约成书于公元前1世纪的《周髀算经》就记录了“勾三股四弦五”的规律(图6.6.6),但没有给出完整的证明,三国时期的赵爽就这一图解补写了一个漂亮的证明,大致意思是4个直角三角形(ab/2)和一个小正方形(b-a)2加起来等于c2。
尽管赵爽的证明看起来比毕达哥拉斯学派的证明优美得多,但并不能掩盖中国古代数学与希腊几何学的明显差异。
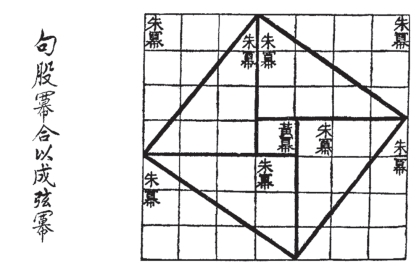
图6.6.6 《周髀算经》中的勾股定理
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




