数据分析、假设检验：众筹融资、网络关系与创业

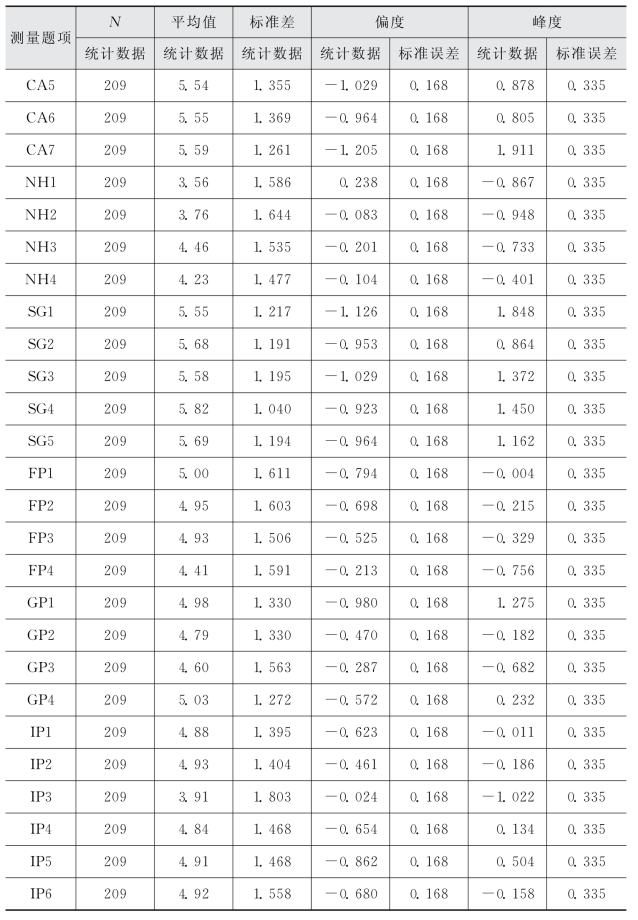
（一）描述性统计分析

在对通过调查问卷方法收集到的数据进行信度效度分析、验证性因子分析以及结构方程建模分析之前，为了判断数据的整体分布特征是否符合正态分布，需要对数据的均值、标准差、偏度和峰度进行描述性统计分析。本研究运用SPSS软件对此次调查所收集到的数据进行描述性统计分析，结果如表3．5所示，所有数据偏度和峰度的绝对值都小于2。结果表明该数据与正态分布基本一致，可以用于进一步的统计分析。

表3．5　各观察变量的描述性统计分析结果

续表

（二）信度分析

信度（reliability）是衡量测量结果的一致性、稳定性及可靠性的指标，目前比较常用的是Cronbach'sα系数法，用于检验测量结果的内部一致性。一般认为，当量表的Cronbach'sα系数值超过0．7时，则可以认为量表数据有良好的内部一致性。本研究同时采用了校正项总相关系数CITC来考察测量结果的内部一致性。一般认为，当测量指标的CITC值大于0．5，最低可接受范围为0．35，同时删除某一测量题项后的Cronbach'sα值（Cronbach's Alpha if Item Deleted）小于该量表的整体Cronbach'sα值，则可以认为该量表的测量结果具有良好的内部一致性，能够用于后续的统计分析。

1．效果推理的信度分析

按照上述方法对效果推理的数据实行了信度分析，结果见表3．6，全部12个测试题项的CITC值都大于0．5，且删除该题项后的Cronbach'sα值均小于该变量的Cronbach'sα值。变量的整体Cronbach'sα值大于0．7。可以认为对效果推理的测量信度良好。

表3．6　效果推理的信度检测结果（N＝209）

2．因果推理的信度分析

按照上述方法对因果推理的数据实行了信度分析，结果见表3．7，全部9个测试题项的CITC值都大于0．5，且删除该题项后的Cronbach'sα值均小于该变量的Cronbach'sα值。变量的整体Cronbach'sα值大于0．7。可以认为对因果推理的测量信度良好。

表3．7　因果推理的信度检测结果（N＝209）

3．创业绩效的信度分析

按照上述方法对创业绩效的数据实行了信度分析，结果见表3．8，全部14个测试题项的CITC值都大于0．5，且去掉该题项后的Cronbach'sα值均小于该变量的Cronbach'sα值。变量的整体Cronbach'sα值大于0．7，测量信度良好。

表3．8　创业绩效的信度检验（N＝209）

续表

4．网络异质性的信度分析

按照上述方法对网络异质性的数据实行了信度分析，结果见表3．9，全部4个测试题项的CITC值均大于0．5，且去掉该题项后的Cronbach'sα值均小于该变量的Cronbach'sα值。变量的整体Cronbach'sα值大于0．7。可以认为对网络异质性的测量信度良好。

表3．9　网络异质性的信度检验（N＝209）

5．共享目标的信度分析

按照上述方法对共享目标的数据实行了信度分析，结果见表3．10，全部4个测试题项的CITC值均大于0．5，且去掉该题项后的Cronbach'sα值均小于该变量的Cronbach'sα值。变量的整体Cronbach'sα值大于0．7。可以认为对共享目标的测量信度良好。

表3．10　共享目标的信度检验（N＝209）

综上所述，本研究5个变量的测量结果均具有良好的内部一致性，能够用于后续的统计分析。

（三）效度分析

效度（validity）反映了测量工具能准确衡量潜变量的程度，通过内容效度（content validity）和构念效度（construct validity）来评价。本研究依据效果推理和社会网络理论框架，采用在学术界被广泛使用的成熟量表，其中由国外学者开发的量表也都经过国内研究者科学翻译，且经研究证实在我国环境下同样可行，因此可以认为本研究问卷所使用的量表具有良好的内容效度。构念效度是指测量变量的具体方法和操作过程能够反映实际所要测量的变量的程度，通过收敛效度（convergent validity）和区分效度（discriminant validity）来评价。

收敛效度是指同一潜变量的所有测量题项之间应具有较高的相关关系，区分效度是指不同潜变量之间应具有显著的差异。通过考察总体量表中各测量题项的因子负荷，以及各量表的平均提取方差值（average of variance extracted，AVE），来检验各量表的收敛效度。一般来说，测量题项在潜变量上的标准化因子负荷需大于0．5且显著。平均提取方差值AVE是计算潜在变量的测量题项的变异解释能力的指标，若AVE越高，则表示构念的收敛效度越高。一般来说须大于0．5，0．36～0．5为可接受门槛。为检验各变量间的区分效度，本文对4个变量进行了验证性因子分析，在基本模型与竞争模型之间进行比较，并采用了χ2／df，RMSEA，GFI，CFI和TLI等拟合度指标来评价模型的适度。

1．收敛效度

本节运用AMOS23．0软件，得到总体测量模型中各测量题项的因子负荷，并人工计算每个量表的平均提取方差值，以此来检验各量表的收敛效度，计算结果如表3．11所示。计算结果显示，所有题项在潜变量上的标准化因子负荷均大于0．5，并且在P＜0．001水平上显著；各个变量的AVE值均大于0．36，为可接受范围。以上结果表明同一量表中各测量题项之间有良好的相关性，本研究所采用的量表均具有良好的收敛效度。

表3．11　总体测量模型收敛效度检验（N＝209）

续表

注：＊＊＊P＜0．001。

2．模型拟合度检验

为检验总体结构方程模型的拟合程度，本文进行了拟合度检验并采用了如表3．12所示指标。

表3．12　结构方程模型总体拟合度评价指标及其标准

模型拟合度检验结果为：χ2／df=2．589，小于3；RMSEA=0．068，小于0．08适配合理；GFI=0．818，大于0．8为可接受范围，CFI=0．918，TLI=0．949均大于0．9，拟合优度较好。

3．区分效度

为了检验“效果推理”“因果推理”“网络异质性”“共享目标”和“创业绩效”5个变量之间的区分效度，本文进行了验证性因子分析，将原模型（五因子模型）和合并因子后的竞争模型（四因子模型、三因子模型、二因子模型、单因子模型）进行对比，比较不同模型的拟合优度指标，结果如表3．13所示。结果显示五因子模型（χ2=2 150．873，χ2／df=2．659，RMSEA=0．068，GFI=0．818，CFI=0．918，TLI=0．949）的拟合优度比其他竞争模型都好，说明本文的研究模型具有良好的区分效度。其中EF为效果推理，CA为因果推理，NH为网络异质性，SG为共享目标，EP为创业绩效，“+”表示将2个因子合并为一个因子。

表3．13　区分效度检验（N＝209）

续表

（四）相关性分析

表3．14为各变量的均值、标准差和相关系数。其中，效果推理与创业绩效（r=0．493，P＜0．01）和网络异质性（r=0．339，P＜0．01）显著正相关，网络异质性和创业绩效显著正相关（r=0．355，P＜0．01），这为假设1、假设2、假设3的成立提供了初步证据；因果推理与创业绩效（r=0．551，P＜0．01）和共享目标（r=0．632，P＜0．01）显著正相关，共享目标和创业绩效显著正相关（r=0．419，P＜0．01）。这为假设5、假设6、假设7的成立提供了初步的证据。

表3．14　描述性统计和相关关系

注：＊＊P＜0．01，＊P＜0．050。

（五）结构方程模型分析

样本分布分析、描述性统计分析和信度效度分析结果说明本研究的数据已经达到了科学研究的标准，可以用来进行进一步的研究。本节将通过结构方程建模方法以及层次回归方法，对前文提出的理论假设进行逐一检验。总共包括4个部分：直接效应检验（假设1、假设2、假设3、假设5、假设6、假设7）、中介效应检验（假设4、假设8）、调节效应检验（假设9）。

1．直接效应的结构方程模型分析

对于直接效应，本文通过结构方程建模方法，进行了两部分内容的检验：一是直接效应的显著性指标，判断影响效应是否显著；二是拟合效果的分析，计算各测量量表的χ2／df、RMSEA、GFI、CFI和TLI值，检验模型的拟合效果。一般认为，显著性指标P＜0．001，说明影响效应显著；拟合效果指标的范围或临界值同表3．11所述。

（1）效果推理对创业绩效的影响效应检验。

运用AMOS软件对“效果推理对创业绩效的影响效应”进行结构方程建模，如图3．3所示。模型的拟合度指标：χ2=858．829，df=294，χ2／df=2．921，RMSEA=0．080，GFI=0．854，CFI=0．920，TLI=0．910；χ2／df＜3，RMSEA＜0．1，GFI＞0．8，CFI和TLI＞0．9，说明模型的拟合效果较好。“效果推理—创业绩效”的标准化路径系数为0．556，在P＜0．001水平下显著，说明这条路径显著。从模型拟合效果和显著性指标看，效果推理对创业绩效有显著的正向影响，即假设1得到了验证。

图3．3　效果推理对创业绩效影响效应的结构方程模型

表3．15　效果推理对创业绩效影响效应的结构方程建模结果

注：＊＊＊P＜0．001。

（2）效果推理对网络异质性的影响效应检验。

运用AMOS软件对“效果推理对网络异质性的影响效应”进行结构方程建模，如图3．4所示。模型的拟合度指标：χ2=278．054，df=99，χ2／df=2．809，RMSEA=0．076，GFI=0．851，CFI=0．945，TLI=0．935；χ2／df＜3，RMSEA＜0．08，GFI＞0．8，CFI和TLI＞0．9，说明模型的拟合效果较好。“效果推理—网络异质性”的标准化路径系数为0．264，在P＜0．001水平下显著，说明这条路径显著。从模型拟合效果和显著性指标看，效果推理对网络异质性有显著的正向影响，即假设2得到了验证。

图3．4　效果推理对网络异质性影响效应的结构方程模型

表3．16　效果推理对网络异质性影响效应的结构方程建模结果

注：＊＊＊P＜0．001。

（3）网络异质性对创业绩效的影响效应检验。

运用AMOS软件对“网络异质性对创业绩效的影响效应”进行结构方程建模，如图3．5所示。模型的拟合度指标：χ2=358．718，df=134，χ2／df=2．677，RMSEA=0．072，GFI=0．888，CFI=0．936，TLI=0．926；χ2／df＜3，RMSEA＜0．08，GFI＞0．8，CFI和TLI均大于0．9，说明模型的拟合效果较好。“网络异质性—创业绩效”的标准化路径系数为0．204，在P＜0．001水平下显著，说明这条路径显著。从模型拟合效果和显著性指标看，网络异质性对创业绩效有显著的正向影响，即假设3得到了验证。(www.xing528.com)

图3．5　网络异质性对创业绩效影响效应的结构方程模型

表3．17　网络异质性对创业绩效影响效应的结构方程建模结果

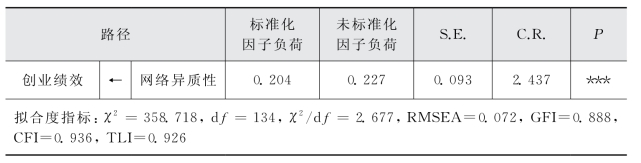
注：＊＊＊P＜0．001。

（4）因果推理对创业绩效的影响效应检验。

运用AMOS软件对“因果推理对创业绩效的影响效应”进行结构方程建模，如图3．6所示。模型的拟合度指标：χ2=634．809，df=188，χ2／df=3．377，RMSEA=0．071，GFI=0．841，CFI=0．922，TLI=0．938；χ2／df＜3，RMSEA＜0．1，GFI＞0．8，CFI和TLI＞0．9，说明模型的拟合效果较好。“因果推理—创业绩效”的标准化路径系数为0．632，在P＜0．001水平下显著，说明这条路径显著。从模型拟合效果和显著性指标看，因果推理对创业绩效有显著的正向影响，即假设5得到了验证。

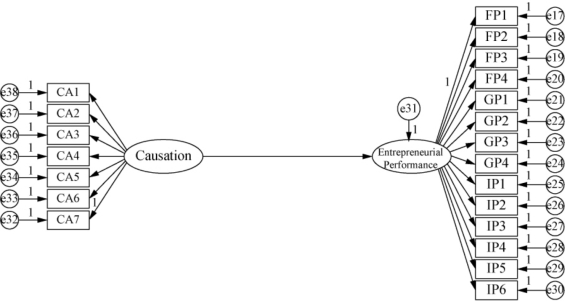
图3．6　因果推理对创业绩效影响效应的结构方程模型

表3．18　因果推理对创业绩效影响效应的结构方程建模结果

注：＊＊＊P＜0．001。

（5）因果推理对共享目标的影响效应检验。

运用AMOS软件对“因果推理对共享目标的影响效应”进行结构方程建模，如图3．7所示。模型的拟合度指标：χ2=166．510，df=53，χ2／df=3．142，RMSEA=0．071，GFI=0．881，CFI=0．902，TLI=0．918；χ2／df＜3，RMSEA＜0．08，GFI＞0．8，CFI和TLI＞0．9，说明模型的拟合效果较好。“因果推理—共享目标”的标准化路径系数为0．730，在P＜0．001水平下显著，说明这条路径显著。从模型拟合效果和显著性指标看，因果推理对共享目标有显著的正向影响，即假设6得到了验证。

图3．7　因果推理对共享目标影响效应的结构方程模型

表3．19　因果推理对共享目标影响效应的结构方程建模结果

注：＊＊＊P＜0．001。

（6）共享目标对创业绩效的影响效应检验。

运用AMOS软件对“共享目标对创业绩效的影响效应”进行结构方程建模，如图3．8所示。模型的拟合度指标：χ2=617．644，df=151，χ2／df=4．090，RMSEA=0．074，GFI=0．832，CFI=0．950，TLI=0．941；χ2／df＜5，RMSEA＜0．08，GFI＞0．8，CFI和TLI＞0．9，说明模型的拟合效果较好。“共享目标—创业绩效”的标准化路径系数为0．478，在P＜0．001水平下显著，说明这条路径显著。从模型拟合效果和显著性指标看，共享目标对创业绩效有显著的正向影响，即假设7得到了验证。

图3．8　共享目标对创业绩效影响效应的结构方程模型

表3．20　共享目标对创业绩效影响效应的结构方程建模结果

注：＊＊＊P＜0．001。

2．中介效应的结构方程模型分析

运用结构方程及建模法检验中介效应分为三个步骤，如图3．9所示，其中X为自变量，Y为因变量，M为中介变量。

图3．9　中介效应检验程序

步骤一，构建自变量和因变量的结构方程模型，检验两者间路径系数c的显著性。若显著，则进行下一步骤；若不显著，则自变量与因变量相关性不显著，停止中介效应分析。

步骤二，构建中介变量中介效应的结构方程模型，检验自变量到中介变量的路径系数a，和中介变量到因变量的路径系数b的显著性。

步骤三，若两系数均显著，则检验自变量到因变量的路径系数c′显著性，若显著，则部分中介效果显著，若不显著，则完全中介效果显著；若两系数至少有一个不显著，则需进行Sobel检定，若Sobel检定结果显著，则部分中介效果显著，若不显著，则不具备中介效果。

（1）网络异质性对“效果推理—创业绩效”关系的中介效应检验。

步骤一的检验结果如表3．21所示，路径系数显著，表明自变量和因变量之间有显著相关性，可以进行下一步分析。步骤二的中介效应结构方程模型如图3．10所示，模型拟合度指标：χ2=1 060．625，df=398，χ2／df=2．665，RMSEA=0．076，GFI=0．830，CFI=0．958，TLI=0．936；χ2／df＜3，RMSEA＜0．08，GFI＞0．8，CFI和TLI均大于0．9，拟合效果良好。显著性检验结果如表3．21所示，其中“效果推理—网络异质性”和“网络异质性—创业绩效”的路径系数均显著。且加入网络异质性之后，“效果推理—创业绩效”的路径系数由β=0．890（P＜0．001）降低为β=0．869（P＜0．05），显著性明显降低，由此可见网络异质性对效果推理与创业绩效之间的关系起到了部分中介的作用，假设4被部分验证。

图3．10　网络异质性对“效果推理—创业绩效”关系的中介效应的结构方程模型

表3．21　网络异质性对“效果推理—创业绩效”关系的中介效应的结构方程建模结果

注：＊＊＊P＜0．001，＊P＜0．050。

（2）共享目标对“因果推理—创业绩效”关系的中介效应检验。

步骤一的检验结果如表3．22所示，路径系数显著，表明自变量和因变量之间有显著相关性，可以进行下一步分析。步骤二的中介效应结构方程模型如图3．11所示，模型拟合度指标：χ2=898．466，df=296，χ2／df=3．035，RMSEA=0．069，GFI=0．826，CFI=0．927，TLI=0．967；χ2／df＜5，RMSEA＜0．08，GFI＞0．8，CFI和TLI均大于0．9，拟合效果良好。显著性检验结果如表3．22所示，其中“因果推理—共享目标”和“因果推理—创业绩效”的路径系数均显著。且加入网络异质性之后，“因果推理—创业绩效”的路径系数由β=0．813（P＜0．001）降低为β=0．756（P＜0．050），相关系数和显著性明显降低，由此可见共享目标对因果推理与创业绩效之间的关系起到了部分中介的作用，假设8被部分验证。

图3．11　共享目标对“因果推理—创业绩效”关系的中介效应的结构方程模型

表3．22　共享目标对“因果推理—创业绩效”关系的中介效应的结构方程建模结果

注：＊＊＊P＜0．001，＊P＜0．050。

（六）中介效应检验

以上通过结构模型建构检验中介效应的方法尚未得到学术界的一致认同。为更审慎地检验网络异质性和共享目标的中介作用，本研究采用层次回归法，分三个步骤对中介效应进行了再次检验。

（1）网络异质性对“效果推理—创业绩效”关系的中介效应验证。

步骤一，检验自变量对结果变量的影响。在引入控制变量（企业规模、成立年限、创业经验）的基础上，将自变量放入回归方程，检验效果推理对创业绩效的影响。

步骤二，检验自变量对中介变量的影响。在引入控制变量的基础上，将自变量放入回归方程，检验效果推理对网络异质性的影响。

步骤三，检验中介效应。在引入控制变量和自变量的基础上，将中介变量放入回归方程，检验效果推理和网络异质性对创业绩效的影响。结果如表3．23所示。

由模型4可知，效果推理对创业绩效有显著的正向影响（M4：β=0．609，P＜0．001），假设1再次得到验证。由模型2可知，效果推理对网络异质性有显著的正向影响（M2：β=0．444，P＜0．001），假设2再次得到验证。对比模型4和模型5，在引入网络异质性之后，效果推理对创业绩效的影响由0．609下降为0．536，显著性由在0．1%的显著性水平上显著变为在5%的显著性水平上显著，显著性明显降低。而网络异质性对创业绩效有显著影响（M5：β=0．164，P＜0．001）。因此网络异质性在效果推理与创业绩效的关系中起到部分中介作用。

表3．23　网络异质性的中介效应检验（N＝209）

注：＊＊＊P＜0．001，＊＊P＜0．01，＊P＜0．050。

（2）共享目标对“因果推理—创业绩效”关系的中介效应验证。

步骤一，检验自变量对结果变量的影响。在引入控制变量（企业规模、成立年限、创业经验）的基础上，将自变量放入回归方程，检验因果推理对创业绩效的影响。

步骤二，检验自变量对中介变量的影响。在引入控制变量的基础上，将自变量放入回归方程，检验因果推理对共享目标的影响。

步骤三，检验中介效应。在引入控制变量和自变量的基础上，将中介变量放入回归方程，检验因果推理和共享目标对创业绩效的影响。结果如表3．24所示。

由模型4可知，因果推理对创业绩效有显著的正向影响（M4：β=0．552，P＜0．001），假设5再次得到验证。由模型2可知，因果推理对共享目标有显著的正向影响（M2：β=0．638，P＜0．001），假设6再次得到验证。对比模型4和模型5，在引入共享目标之后，因果推理对创业绩效的影响由0．552下降为0．464，显著性由在0．1%的显著性水平上显著变为在5%的显著性水平上显著，显著性明显降低。而共享目标对创业绩效有显著影响（M5：β=0．137，P＜0．001）。因此共享目标在因果推理与创业绩效的关系中起到部分中介作用。

表3．24　共享目标的中介效应检验（N＝209）

注：＊＊＊P＜0．001，＊＊P＜0．01，＊P＜0．050。

（七）调节效应检验

本节采用层次回归法验证共享目标对网络异质性与创业绩效关系的调节作用，分三个步骤进行。

步骤一，考虑到控制变量（企业规模、成立年限、创业经验）可能对因变量（创业绩效）产生影响，因此首先将控制变量引入回归方程。

步骤二，在放入控制变量的基础上，将自变量（网络异质性）和调节变量（共享目标）同时放入回归方程中。

步骤三，在步骤二的基础上，将自变量和调节变量的交互项放入回归方程。层次回归分析的结果如表3．25所示。

由模型1可知，控制变量中仅企业规模对创业绩效的影响显著。企业成立年限和创业者创业经验对创业绩效的影响不显著。由模型2可知，网络异质性（β=0．248，P＜0．001）和共享目标（β=0．392，P＜0．001）对创业绩效均有显著影响，且R2显著提升，说明模型对整体的解释度显著提升。由模型3可知，网络异质性与共享目标的交互项（β=0．580，P＜0．001）对创业绩效有显著的正向影响，表明共享目标对网络异质性与创业绩效之间的关系有正向调节作用。共享目标程度越高，网络异质性与创业绩效之间的正相关关系越强；共享目标程度越弱，网络异质性与创业绩效之间的正相关关系越弱。因此，假设9得到了验证。

表3．25　调节作用回归分析（N＝209）

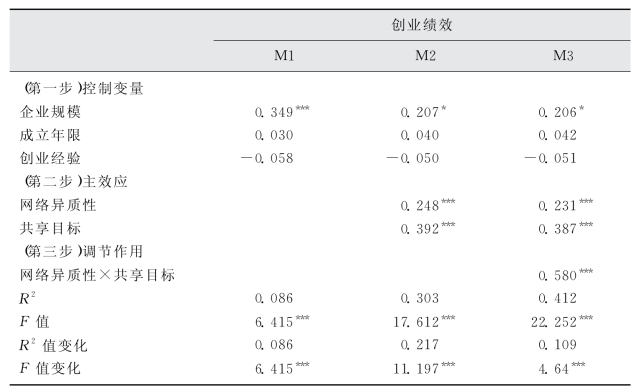
注：＊＊＊P＜0．001，＊＊P＜0．01，＊P＜0．050。

为更直观地展示调节效应，本节采用简单坡度分析法，将共享目标按均值加减一个标准差分为高共享目标和低共享目标两组，分别进行回归分析，得到回归系数，结果如图3．12所示，描绘了当合作企业间目标共享程度不同时，网络异质性对创业绩效的影响。

图3．12　共享目标的调节作用