八年级数学染色问题及方法

费古生，美国现代数学家兼雕塑家，他能用青铜雕塑出美丽的富有数学启发性的艺术品．

这一具有凹槽的造型优美的雕塑，是花托、十字帽和向量场的组合，于1988年创作，现在静静坐落在美国数学会总部的广场上．

知能概述

我们把要求作出或证明存在满足某种染色性质的点、格、线、区域或图形等问题叫染色问题，染色问题一般根据同色点或同色三角形展开分析．

把问题的对象恰当染色，以便观察、分析对象之间的关系，通过对染色图形的分析达到对原问题解决的目的，这种解题方法被称为染色方法．

染色方法是一种形象化的分类讨论方法．

问题解决

例1　对平面上的点染上黑色或白色（称为二染色）．求证：一定存在长为a（a＞0）的线段，它的两个端点同色．

分析　在平面上任画一条长为a的线段AB．若A，B两点同色，则结论已成立；若A，B两点不同色，为确定起见，不妨设A为黑色，B为白色．如图，以AB为边作正三角形ABC，这时，若C为黑点，则线段AC合于题设要求；若C为白点，则线段BC合于题设要求．

上述分析过程，其实已完成了证明．其中作单位正三角形ABC是关键，于是可以找到如下的简化证明方法．

证明　在二染色平面上作一个边长为a的正三角形，设三个顶点为A，B，C，根据抽屉原则，A，B，C三点中必有两点同色，比如A，B两点同色，又AB＝a，线段AB合于题设要求．

例2　用任意的方式，将平面上的每个点染黑色或白色．求证：一定存在一个边长为1或的正三角形，它的三个顶点同色．

我从人类原始数学文化的源泉中发掘材料，用我的雕塑把这些数学信息送向遥远的未来．

——费古生

二色定理

1840年德国几何学家莫比乌斯提出如下问题：平面上有n条直线把平面分成若干区域，能否用黑白两种颜色来染色，使任意两个相邻的区域（指有公共边界的区域）都染上不同的颜色？

该问题的结果被称为二色定理．

证明　若存在边长为1且顶点同色的正三角形，则问题得证．

若不存在边长为1且顶点同色的正三角形，则一定存在长为1的线段AB，两端点A，B异色．

以AB＝1为底作腰长为2的等腰△ABC，则点C与A或B总有一对是异色的．如图①，不妨设长为2的线段AC两端点异色．

图①

图②

取AC的中点O，则O必与A，C之一同色（如图②，不妨设O与A同色）．由于不存在边长为1的顶点同色的正三角形，于是，以AO为一边的等边三角形的另外的顶点D和E必与A异色．此时，△ECD就是一个边长为的顶点同色的正三角形．

例3　空间六点，任三点不共线，任四点不共面，成对地连接它们得十五条线段，用红色和蓝色染这些线段（一条线段只染一种颜色），求证：无论怎样染，总存在同色三角形．

证明　设A，B，C，D，E，F是所给六点．考虑以A为端点的线段AB，AC，AD，AE，AF，由抽屉原理知这五条线段中至少有三条颜色相同，不妨设就是AB，AC，AD，且它们都染成红色，再来看△BCD的三边，如其中有一条边是红色的（例如BC边），则同色三角形已出现（红色△ABC）；如△BCD三边都不是红色的，则它就是蓝色三角形，同色三角形也出现了．总之，不论在哪种情形下，都存在同色三角形．

例4　请你将下图中的5个图形拼成一个4×5的长方形，能完成吗？

分析　画出4×5的长方形，并将它分别涂上黑白两色，如图．试着把A，B，C，D放到长方形上，就会看到，不管怎么放，它们必定盖住两个黑正方形和两个白正方形．于是，前4块盖住的是8个黑正方形和8个白正方形．可是，对于E，情况就不同了，它总是盖住一种颜色的3个正方形和另一种颜色的1个正方形，而图中共有10个黑正方形和10个白正方形．无论把A，B，C，D摆在什么地方，它们必定盖住8个黑正方形和8个白正方形，然后E盖的是两个黑正方形和两个白正方形，然而E不能盖住两个白正方形和两个黑正方形．所以，我们用A，B，C，D，E五个图形不能拼成一个4×5的正方形．

染色问题有下列基本形式：

（1）按某种特定要求，构造出符合条件的染色图形，或给出染色方案；

（2）对一些任意染色图形，说明其存在的必然性．

对于例3，若视六点为六个人，两点连红线表示两人认识，两点连蓝线表示两人不认识，就得到一个变式命题：任何六个人中，一定有三个人或者互相都认识，或者互相都不认识．

国际象棋棋盘，交替染色是最直观、最常见的染色模型．通过对对象的染色，对象间的隐含关系变得明朗．当基本的交错染色方法失效时，寻找新的染色方法是解决问题的关键．

例5　120人参加数学竞赛，试题共有5道大题．已知第1，2，3，4，5题分别有96，83，74，66，35人做对．如果至少做对3题便可获奖，问：这次竞赛至少有多少人获奖？

（江西省竞赛题）

解　将这120人分别编号为P1，P2，…，P120，并视为数轴上的120个点．用Ak（k＝1，2，3，4，5）表示这120人之中未答对第k题的人所成的组，｜Ak｜为该组的人数．则｜A1｜＝24，｜A2｜＝37，｜A3｜＝46，｜A4｜＝54，｜A5｜＝85．

将以上五个组分别赋予五种颜色，如果某人未做对第k（k＝1，2，3，4，5）题，则将表示该人的点染第k色．

问题转化为：求出至少染有三色的点最多有多少个．

由｜A1｜＋｜A2｜＋｜A3｜＋｜A4｜＋｜A5｜＝246知至少染有三色的点不多于＝82个．

一方面，将点P1，P2，…，P85这85个点染第5色，因85＞82，而为使染有三色的点数尽可能多，需在上述85个点中将尽可能多的点再加染另两色，由于｜A1｜＋｜A2｜＋｜A3｜＋｜A4｜＝161，故加染另两色的点不会多于＝80个，即染有三色的点不多于80个．

另一方面，可以具体构造一种染法，使得有80个点染有三种颜色．例如，如图，将点P1，P2，…，P85这85个点染第5色；点P1，P2，…，P44以及点P79，P80这46个点染第3色；点P45，P46，…，P81这37个点染第2色；点P1，P2，…，P24这24个点染第1色；点P25，P26，…，P78这54个点染第4色．于是，至少染有三种颜色的点最多有80个．因此，染色数不多于两种的点至少有40个，即至少有40人获奖（他们每人至多答错两题，而至少答对三题，例如，P81，P82，…，P120这40个人）．

喜形于色

把实际问题抽象成染色图的问题，形象而直观，既便于思考分析，又有利于归纳总结．

例6　如图，是一个“L”形的4个小方格，无重叠地铺盖成一个m×n的矩形．试证：m×n必为8的倍数．

（北京市竞赛题）

染色问题的解决和染色方法的运用，常与构造性、奇偶分析、反证法、抽屉原理等方法联系，需要的不是较多的数学知识，而是缜密的思维和较强的推理能力．

寓知识于趣味，融方法于故事，在探索中深入问题，在最意想不到的地方去发现数学的奇妙．

证明　由于每个“L”形有4个小方格，若k个“L”形恰好拼成一个m×n的矩形，则mn＝4k，下面证明即可．

因mn＝4k，故m，n中必有一个为偶数，不妨设m为偶数，把矩形的列交错地涂上黑、白两种颜色，则两种颜色的方格各有2k个，每个“L”形占据奇数个（1个或3个）白格，由于白格的总数是偶数2k，若“L”形纸片为奇数个（即k为奇数），则奇数个奇数之和为奇数，不可能等于偶数2k，所以k必为偶数．

故

1．在一个m行、n列（m≥n）的方格表中，有mn个边长为1的小方格，每个小方格用红、黄、蓝三种颜色中的一种颜色染色．已知方格表的每一行有6个红色的小方格，每一列有8个黄色的小方格，整个方格表共有15个蓝色的小方格．如果n是两位的质数，那么m＝________，n＝________．

（“我爱数学”夏令营竞赛题）

2．用红、黄、蓝三种颜色染3×3表格的每一个方格，使满足：①每行三色都有；②每列三色都有；③邻格（有公共边的两个方格）不同色，则不同的染色方法有（　）种．

A．12　B．18　C．24　D．27

（全国初中数学联赛题）

3．将一条直线进行黑、白二染色，证明：必存在同色的三个点，使得其中一点是另两点为端点的线段的中点．

4．将正十三边形的每个顶点染成黑色或染成白色，每顶点只染成一色．证明：存在三个同色顶点，它们刚好成为一个等腰三角形的顶点．

5．如图，边长为7的正三角形被分成49个边长为1的小正三角形．问：最多可沿图所示的格线划分出多少个邻边长分别为1和2的平行四边形？

（乌克兰数学奥林匹克竞赛题）

（第5题）

（第6题）

（第8题）

6．如图，是半张中国象棋盘，中国象棋的马走“日”字，一匹马从起点A出发跳了n步又回到起点．试证明：n一定是偶数．

7．证明：只用2×2及3×3的两种瓷砖不能恰好铺盖23×23的正方形地面．(www.xing528.com)

8．如图，有一个正方形的铁丝架，把它的侧棱中点I，J，K，L也用铁丝连上．

（1）现有一个蚂蚁想沿着铁丝从A点爬到G点，问最近的路线一共有几条？并用字母把这些路线表示出来（用所经过的连接点字母来表示，譬如蚂蚁从A点出发，经过I点、L点，最后达到H点，这样的路线用AILH表示）．

（2）蚂蚁是不是可能从A点出发，沿着铁丝经过每一个连接点恰好一次，最后到达G点？如果可能，请找出一条这样的路线；如果不可能，说明为什么．

（江苏省竞赛题）

9．圆周上等间距地分布着27个点，它们被分别染为黑色或白色．今知其中任何2个黑点之间至少间隔2个点．证明：从中可以找到3个白点，它们形成等边三角形的3个顶点．

（俄罗斯圣彼得堡数学奥林匹克竞赛题）

10．将正2014边形的每一条对角线染上一种颜色，且要求任意两条在形内相交的对角线不同色，试求使用颜色数目n的最小值．

（英国数学竞赛题）

11．有足够多如图所示的三种拼板，用它们来覆盖一张9×11的棋盘，拼板的边必须与棋盘的网格线重合，且任意两片拼板都互不重叠，请问至少需要三单位正方形的那种拼板多少片？

（国际中小学数学能力检测题）

1．17，13　6m＋8n＋15＝mn，（m－8）（n－6）＝63＝1×63＝3×21＝7×9，而n是两位的质数，故m＝17，n＝13．

2．A　用A，B，C分别代表红、黄、蓝三色，为叙述方便，将各方格分别编号1，2，…，9（如图）．

考虑左上角形如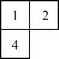的格，则1号格有A，B，C三种染色．先设染为A色：，则2，4格共有4种染法：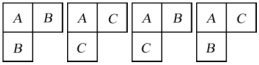

（第2题）

而当1，2，4号格的染色都确定后，其他格的染色情况便唯一确定；

由于每行三色都有，每列三色都有，则3，7号格染色情况随之确定．

又因2，3与5，6四格中所用的颜色数等于3，必有某种颜色要用两次，为避免同色格相邻，则5，6号格只有一种染法；而当前两行的格都染好后，第三行的每格颜色便随之确定．

因此，1号格染为A色时，全表有4种染法．

据对称性，当1号格染为B色或C色时，全表也各有4种染法．因此，共有12种染法，故选A．

3．将一条直线l黑、白二染色，直线l称为二染色直线．

在二染色直线l上任取三点，必有两点同色，不妨设A，B两点同为黑色，记AB的中点为C．

（1）若C为黑色，则结论已成立（图①）．

（2）若C是白点，在二染色直线l上再取D，E两点，使DA＝AB＝BE．

①若D，E中有黑点，比如D为黑点，则D，A，B三点合乎要求（图②）；

②若D，E均为白点，则D，C，E三点合乎要求（图③）．

（第3题）

4．设其13个顶点依次为A1，A2，…，A12，A13，若13个顶点都染成黑色或都染成白色，则结论显然成立．故只需考虑13个顶点中有染黑色也有染白色的情形．这时必有相邻两顶点同色，不妨设A1，A2同色．现考虑A13，A1，A2，A3，A8这5个顶点，由抽屉原理知其中必有三顶点同色，这又分为下列三种情形：

（1）A13，A1，A2，A3中有三点同色．已知A1，A2同色，则A13，A1，A2同色或A1，A2，A3同色．这时△A13A1A2或△A1A2A3即为三顶点同色的等腰三角形．

（2）A13，A3，A8同色，这时△A13A3A8为三顶点同色的等腰三角形．

（3）A1，A2，A8同色，这时△A1A2A8为三顶点同色的等腰三角形．

5．如图①，将49个小正三角形黑白相间地进行染色．

（第5题）

由于每个邻边长为1和2的平行四边形必须要包含2个白色的小三角形，又一共有21个白色小三角形，故满足题意的平行四边形的数目不超过10．

图②给出了一种划分出10个平行四边形的方法．

6．如图所示，在各交点涂上黑、白色．“马”从A点开始跳，起点是黑点，下一步不管怎么跳都是跳到白点，再下一步又跳到黑点……这样，“马”跳到的点的顺序是白、黑、白、黑……“马”要想跳回到起点即黑点，必须要跳偶数步，所以n一定是偶数．

7．将23×23的正方形地面中第1，4，7，10，13，16，19，22列中的小方格全染成黑色，剩下的小方格全染成白色，于是白色的小方格个数为15×23，这是一个奇数，因为每块2×2瓷砖总是盖住两黑格和两白格或者盖住四白格，每块3×3的瓷砖总是盖住三黑格和六白格．故无论多少2×2及3×3的瓷砖盖住的白格数总是一个偶数，不可能盖住15×23个白格，所以只用2×2及3×3的瓷砖不能盖住23×23的地面．

（第6题）

8．（1）一共有12条：ABCKG，ABJKG，ABJFG，ADCKG，ADLKG，ADLHG，AIJKG，AIJFG，AILKG，AILHG，AIEFG，AIEHG．

（2）不可能．如图将所有连接点染上黑白两色，凡与黑色相邻的都是白点，凡与白点相邻的都是黑点．

蚂蚁从黑点A出发，依次走过其他各点，由于一共有12个连接点，因此必须经历一条形如黑→白→黑→白→…→黑→白的路线，但现在G点也为黑点，所以蚂蚁不可能从A点出发，经过每一个连接点恰好一次，最后到达G点．

9．我们将27个点依次编号，则它们一共可以形成9个正三角形（1，10，19），（2，11，20），…，（9，18，27）．由染色规则知，其中至多有9个黑点．

若黑点不多于8个，则其中必有一个正三角形的所有顶点全为白色；若黑点恰有9个，则它们只能是一黑两白相间排列，其中也一定有一个正三角形的所有顶点全为白色．

（第8题）

10．若将连接正2014边形中正对着的两个顶点的对角线称为主对角线，则该多边形共有1007条主对角线，且这些主对角线交于一点，即正2014边形的中心．所以，至少需要1007种颜色．

接下来构造一个只用1007种颜色的图形满足题目要求．

令每一条从主对角线两个顶点出发且按顺时针方向连接得到的对角线与该主对角线同色，如图．

由此，可将多边形的每一条对角线均染上颜色，同时，由于具有相同颜色的对角线均在与其同色的主对角线的两侧，且只能在主对角线的顶点处相交，从而，上述图形中不存在两条在形内相交且同色的对角线．

综上，满足条件的颜色数目n的最小值为1007．

11．如图①所示，将棋盘上位于奇数行奇数列的小正方形涂成灰色，共有5×6＝30个灰色正方形．

（第10题）

（第11题）

显然，在给定的三种方块中，每一片方块至多可以覆盖1个红色正方形．因此至少需要30多片方块才可以覆盖整张棋盘．如果“L”形三方块使用了m片，另两种四方块共享了n片，那么

m＋n≥30．①

现在，每片“L”形三方块可以覆盖棋盘上3个正方形，另外两种四方块每片可以覆盖4个正方形，则

3m＋4n＝9×11＝99．②

根据①式，可得4n＝99－3m，

根据②式，得4m＋4n≥120，

因此4m＋（99－3m）≥120，

解得m≥21．即“L”形方块的数目不能小于21，如图②是恰使用21片“L”形方块的摆放方法．

（第11题）

综上所述，至少需要21片“L”形方块．