八年级数学教材：图论思想及应用

18世纪的哥尼斯堡城，有如左图所示的七座桥，连接着两岸（C，D）、河心岛（B）、半岛A．有人提出一个问题：能不能一次不重复地走遍所有七座桥，最后仍回到出发点？欧拉把实际中的“七桥问题”抽象成一笔画模型，以深邃的洞察力证明了这样的走法不存在，并于1736年公布了自己的研究结果．

知能概述

事物之间总存在某种关系，为了研究事物的关系，我们用点来表示事物对象，若两个对象之间存在某种关系，则用一条线把相应的点连接起来，这样就得到一个由点、线组成的图，通过研究图的性质探索出事物的关系，就是图论的基本思想．

对图的研究只关注线的关系，而不注重线的长短、曲直．

图论是一门古老的数学分支，主要研究用某种方式联系起来的若干事物之间的二元或多元关系，图论的引进改变了计算机科学、网络等领域的面貌．

问题解决

例1　A，B，C，D，E，F六个足球队进行单循环比赛，当比赛到某一天时，统计出A，B，C，D，E五队已分别比赛了5，4，3，2，1场球，则还没有与B队比赛的球队是________．

（江苏省竞赛题）

解题思路　用算术或代数法解，易陷入困境．用6个点表示A，B，C，D，E，F这6个足球队，若两队已经赛过一场，就在相应的两个点之间连一条线，这样用图来辅助解题，形象而直观．

如果一个特定的问题可以被转化为一个图形，那么思想就整体地把握了问题，并且能创造性地思索问题的解法．

——斯蒂恩

周游世界

哈密顿（1805—1865），英国数学家、物理学家，下面问题出自哈密顿之手．

一位旅行家打算做一次环游世界的旅行，他选择了20个城市作为游览点，这20个城市恰好均匀地分布在地球上，而每个城市均有三条航线或道路与其他毗邻城市连接，城市分布及航路如图．问：如何安排一条旅游路线，使这位旅行家可以不重复地游览完每一个城市后再回到出发点？

例2　下面的图形，共有（　）个可以一笔画（不重复也不遗漏；下笔后笔不能离开纸）．

A．0　B．1　C．2　D．3

（“五羊杯”竞赛题）

解题思路　略

例3　证明：在任何一群人中，认识这群人中奇数个人的人有偶数个．

证明　用点v1，v2，…，vn表示这群人，两个人互相认识就连一条边，则每个人认识人的个数就是该点的引线条数，记为d（vi）．若图中有n条边，由于每条边都有两个端点，因而d（v1）＋d（v2）＋…＋d（vn）的计算中，每条边都被重复计算了两次，得d（v1）＋d（v2）＋…＋d（vn）＝2n．

把左边的偶数都移到右边，可得右边仍为偶数，故左边的奇数必有偶数个，命题得证．

例4　若干台计算机联网，要求：（1）任意两台之间最多用一条电缆连接；（2）任意三台之间最多用两条电缆连接；（3）两台计算机之间如果没有连接电缆，则必须有另一台计算机和它们都连接有电缆．若按此要求最少要连79条．问：（1）参加联网的有多少台计算机？（2）这些计算机按要求联网，最多可以连多少条电缆？

（“华罗庚金杯”少年数学邀请赛试题）

解　将每台计算机当作一个点，如果两台计算机之间有电缆连接，那么就在相应的两个点之间连一条线，得出一个图G．

如果一个图中的任意两个点A，B，都可以沿着图中的线从A走到B，那么这样的图就称为连通图．

由于条件（3），图G是连通图．但一般的连通图不一定符合条件（3），如图就是连通图，但不满足（3）．

显然n个点可以用n－1条线连成连通图：这只要将这些点一个接一个连起来（A与B连，B与C连，……）或将一点A与其他n－1个点相连就可以了．所以80个点（80台计算机）可以用79条线相连，而少于80个点时，可以用少于79条线相连．即（1）的答案是80．

条件（2）说明图G中没有三角形．

我们证明更一般的结论：如果一个图的顶点个数是2n，图中没有三角形，那么图中最多有n2条线．

设顶点A1引出的线最多，与A1相连的顶点有k个，它们是B1，B2，…，Bk．

所谓一笔画，就是要求笔不离纸且一次把图画出，图上的每一条边都要画到而又不准重复．

若一个图可以从任一顶点沿着边走到另一个顶点，这种图叫连通图．

若一个图是连通的，并且它的聚结奇数条边的点的个数为0个或2个，则这个图能一笔画．

事物之间总存在某种关系．如人之间，相识或不相识；城市之间，有公路相通或无公路相通；国家之间，相邻或不相邻．

抽象出的图形象而直观，易借助图形展开推理．

运用图论思想解题的关键是：能将原问题转化为图，能正确分析图．

这时，B1不能与B2，…，Bk中任何一个相连（否则产生三角形，顶点是A1，B1及B2，…，Bk中的一点），所以B1至多引出2n－k条线．同理，B2，…，Bk也是如此，它们一共引出≤（2n－k）k条线．

对于B1，B2，…，Bk之外的点，每一个至多引出k条线，所以它们一共引出≤k（2n－k）条线，从而图中的线≤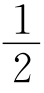［（2n－k）k＋k（2n－k）］＝k（2n－k）条（前面的系数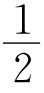是因为上述过程中，每条线被算了2次），而k（2n－k）＝－n2＋2nk－k2＋n2＝n2－（n－k）2≤n2．所以图中的线数≤n2．

当且仅当k＝n，并且2n个顶点分成两组，第一组n个点A1，A2，…，An，第2组n个点B1，B2，…，Bn，同一组的点之间不相连接，不同组的点之间互相连接（即Ai与Aj，Bi与Bj不相连接，而Ai与Bj互相连接，i，j＝1，2，…，n）．这时图中没有三角形，并且共有n2条线．

在本例中，2n＝80，所以n2＝1600，即最多可以连1600条电缆．

拉姆赛定理

1958年《美国数学月刊》登载了例5这样一个有趣的问题，这个聚会问题就是拉姆赛定理的特例．“任一个足够大的结构中必定包含一个给定大小的子结构”，这是旷世奇才拉姆赛理论的主导精神．

例5　世界上任意6个人聚会，一定有3个人互相认识，或者有3个人互相不认识．

（匈牙利数学奥林匹克竞赛题）

解法1　设A为其中一个人．

如果A认识的人数≥3，设B，C，D与A互相认识．B，C，D中如果有两个人互相认识，例如B，C互相认识，那么A，B，C这3人互相认识．B，C，D中如果每两个人互不相识，那么B，C，D就是互不相识的3个人．

如果A认识的人数＜3，那么A不认识的人至少有3（即5－2）个．设B，C，D都不认识A．B，C，D中如果有两个人互不相识，例如B，C互不相识，那么A，B，C这3个人互不相识．B，C，D中如果每两个人互相认识，那么B，C，D就是互相认识的3个人．

上面所分的两种情况，后一种（如果A认识的人数＜3）与前一种（如果A认识的人数≥3）的推理完全相同，只需将其中不相识改为相识，相识改为不相识．

解法2　用点A1，A2，…，A6代表6个人，两个人互相认识则在对应的两点间连一条红边，否则连一条蓝边．问题转化为图中必有三边同色的三角形．

考虑A1的5条引线，因为只染了两种颜色，由抽屉原理知必有3条同色．不妨设A1A2，A1A3，A1A4同为红色；若A2A3，A3A4，A4A2中有红边，则有红色△A1AiAj（2≤i，j≤4）；若A2A3，A3A4，A4A2无红边，则△A2A3A4为蓝三角形．无论哪种情况，图中都有同色三角形．

对于例5，解法1是用枚举法，解法2是用图论思想，即把所研究的事物抽象成几何中的点，而把两个事物之间的某种关系抽象成点与点间的连线，就可以画出一个图．原问题就等价于所画图形中的一个问题，只需研究所画图形的边、顶点之间的某些性质，就可以使原问题迎刃而解．

1．一个房间住了6个客人，当中至少有一个人没有与房间里的每个人握手，那么房间里可能与每个人都握手的人数的最大值是________．

2．下列各图中，无法不重复地一笔画成的是（　）．

3．有7个代表参加一个会议，已知他们每个人至少认识其中的一个人．证明：必有一个人至少认识其中的两个人．

4．某工厂生产由6种不同颜色的纱线织成的双色布，在这个工厂所生产的双色布中，每一种颜色的纱线至少与3种其他颜色的纱线搭配过．证明：可以挑出3种不同的双色布，它包含有全部6种颜色．

（匈牙利数学奥林匹克竞赛题）

5．大厅中有100个客人，每个人都与其余客人中至少67个人相识．证明：这些客人中一定可以找出4个客人，他们中任何两个人都互相认识．(www.xing528.com)

（波兰数学奥林匹克竞赛题）

6．有17位科学家，其中每一个人和其他所有人通信，通信中讨论的题目总共3个，并且每两个科学家之间只讨论同一个题目．求证：至少有3个科学家之间讨论的是同一个题目．

（国际数学奥林匹克竞赛题）

7．某地区网球俱乐部的20名球员举行了14场单打比赛，每人至少上场一次．求证：必有6场比赛，其12个参赛者各不相同．

（美国数学奥林匹克竞赛题）

8．安娜与杰瑞夫妇与其他四对夫妇参加一个聚会．抵达后，他们中有些人之间相互握手，但是夫妻之间、自己同自己没握过手．随后，杰瑞问聚会中的每一个人：“你同多少人握手了？”他得到9种不同的答案．问：有多少人同安娜握手？

（克罗地亚数学竞赛题）

9．一个国家公园准备建立急救服务系统，各急救站之间由电话线相互联络．每个急救站必须能够同其他所有急救站进行联络，直接联络或者最多通过另一个急救站来联络．每个急救站最多能够通出三条电话线．如图表示这种网络的一个例子，它联络着7个急救站．按这种方式建立的网络系统最多能够联络多少个急救站？

（第9题）

（英国数学奥林匹克竞赛题）

10．某国有n座城市，任意两座城市之间有双向直达航班．已知对任意两座城市，它们之间的两个方向的机票价格相同，不同城市对之间的航班机票价格互不相同．证明：存在由n－1段依次相连的航班，使得各航班机票的价格依次严格单调下降．

（俄罗斯数学竞赛题）

例1　E队　如图所示．

（例1）

例2　C

1．4　设6个客人分别为A1，A2，A3，A4，A5，A6，假设A1与A2没握手，则A1与A2都没有与每个人握手，从而，房间里可能与每个人握手的人数不会超过4．由图可见A3，A4，A5，A6与每个人握手是可以做到的，故与每个人都握手的人数的最大值为4．

2．D　图D中有4个奇顶点，多于2个，故不能一笔画．

（第1题）

（第3题）

3．将7个人表示为7个点A1，A2，…，A7，由于他们每个人至少认识其中的一个人，设A1与A2认识，A3与A4认识，A5与A6认识，得如图所示的3条线段，这时，无论A7与谁认识，都会出现一个顶点引出两条边的情况．

4．将6种颜色作为6个点A，B，C，D，E，F，如果两种颜色相配，就在相应的两个点之间连一条线．这样，每点引出3条线，要证明图中有3条线没有公共端点．

不妨设A，B之间有一条线．因为C与3个点相连，所以C除A，B外，还与一点D相连．

如果E与F相连，那么AB，CD，EF就是所求的3条线．

如果E与F不相连，可设E与A，C，D相连．这时如果F与B相连，那么EA，CD，FB就是所求的3条线；如果F与B不相连，那么F必与A，C，D都相连，EC，FD，AB就是所求的3条线．

在一个有2n个点的图中，如果可以找到n条没有公共端点的线，这n条线就称为这个图的一个匹配．本题就是要找出一个匹配．更一般的，在有2n个顶点的图中，如果每一点至少与n个点相连，那么必有一个匹配．

5．客人A认识67个人，设B是其中的1个，B不认识的人至多100－67－1＝32个，所以A所认识的67个人中，至少有67－1－32＝34个人，B是认识的，设C是其中之一．C不认识的至多32个，所以上述34个人中，去掉C，还有33个人，其中至少有1个人D，是C认识的．

所以A，B，C，D4个人互相认识．

本题的关键是考虑每个人不认识的人至多32个，从A认识的人中找B认识的人（去掉B不认识的人），再从A，B认识的人中，去掉C不认识的．

如果n个点，每两点都连一条线，则所得的图称为完全图或竞赛图，并记为Kn．

本题就是要证明：在100个点的图中，如果每点至少引出67条线，那么图中一定有四个点构成K4．

6．将科学家用点表示．两科学家通信时，就在相应的两点间连一条线，并根据讨论的题目分别染上红、黄、蓝三种颜色．问题即转化为：将完全图K17的线用红、黄、蓝三种颜色染色，证明必有同色三角形．

点A1引出16条线，其中必有6条同一种颜色．不妨设A1A2，A1A3，…，A1A7都是红色．

如果A2，A3，…，A7这6点之间的连线有一条为红色，那么A1与这条线的两个端点构成的三角形是同色三角形，三条边都是红色．

如果A2，A3，…，A7这6点之间的连线都不是红色，那么这6点所成的完全图的线只有黄、蓝两种颜色．必有一个同色三角形．因此结论成立．

7．考虑一个图，有20个顶点，14条边，并且每一个顶点至少引出一条边（即每个人至少上场一次）．

设点vi的次数为di，则d1＋d2＋…＋d20＝2×14＝28．

对每一点vi，去掉自它引出的di－1条边（同一条边可以同时被两个端点去掉），至多去掉（d1－1）＋（d2－1）＋…＋（d20－1）＝d1＋d2＋…＋d20－20＝28－20＝8条边，因而至少剩下14－8＝6条边．由于这时每个点至多引出一条边，所以这6条边的端点互不相同．即有6场比赛，参加比赛的12个人各不相同．

8．没有一个人会与多于8个人握手．则杰瑞得到的答案为：0，1，2，3，4，5，6，7，8．

安娜肯定不会与8个人握手，换言之，如果她与8个人握手，那么，在场的其他人（除杰瑞外）中的每一个人均与她握手．则不会出现答案0．

设同8个人均握手的人是A1．可知，没有同他人握手的唯一的人是A1的配偶，设其为A2．如果假设安娜同7个人握手，则除去杰瑞和A2的所有人均同安娜握手．所以，不会出现答案1（A1也同所有人握手）．

设同7个人均握手的人是B1．可知，给出答案1的那个人是B1的配偶（因为A1、B1与在场的其他人握手），设其为B2．

同理，配偶C1，C2给出的答案是6，2；配偶D1，D2给出的答案是5，3．

由此可知安娜给出的答案是4，即她同4个人握手，如图．

（第8题）

（第9题）

9．在这个问题中给出的例子说明，至少有7个急救站可以用这种方式进行联络．我们首先求出急救站的最多个数，然后验证是否可以构成具有这么多急救站的网络．让我们选取一个特定的急救站，把它看作基地．它可以同另外1个、2个或3个急救站联络，如图①所示．（考虑到可能存在三条电话线并未完全使用的基地，就是说A，B和C不一定不同．）急救站A，B和C中的每一个都还有两条未使用的电话线，因而每一个都能再与两个急救站联络，如图②所示．（同样图中所示急救站不一定不同．）现在，不可能再增加急救站了，因为再增加的任何急救站都不可能与基地“紧密”联络，即最多通过另一急救站联络．这说明网络中的急救站不能多于10个．现在来验证是否可以建立包含了10个急救站的网络．在图中，只有基地能与其他急救站紧密联络，例如，A距离B和C以外联络的急救站D，E，F，G“太远了”．但是这些外面的急救站中的每一个还有两条未使用的电话线，可以使用这些电话线把外面的急救站与所有的急救站紧密联络．这要求试凑着进行，最后确定会得到含有10个急救站的网络系统，如图③所示．

注：有趣的是，这个特定的网络图就是著名的彼得松图，这种图在一些看来并无联系的方面都会出现．然而其表示方式可能与图②不同，通常如图④所示．

10．用AB表示从城市A出发到城市B的航线．对任何一座城市A按如下方法构造一条从城市A出发的由航线组成的道路．

设A0＝A，A0A1的机票价格a1在所有从城市A0出发的航班中最高，A1A2的机票价格a2在所有从城市A1出发且机票价格小于a1的航班中最高……如此下去，直到某座城市Ak，使得所有从城市Ak出发的航班机票价格均大于ak．

于是，一共得到n条道路．

下面证明任意航班BC均会出现在某条道路中．

令B1＝B，B0＝C，b1为BC的机票价格．

设B2B1的机票价格b2在所有以城市B1为终点且机票价格大于b1的航班中最低，B3B2的机票价格b3在所有以城市B2为终点且机票价格大于b2的航班中最低……如此下去，直到某个BkBk－1在所有以城市Bk为终点的航班中机票价格最高．

从城市Bk出发的由航线组成的道路将依次路过Bk，Bk－1，…，B1（＝B），B0（＝C）．

由前面得到共n条道路包含了所有的共2C2n＝n（n－1）个航班．

故其中有一条道路至少含n－1个航班．