在自然界中，在建筑艺术中，在抽象图形中，对称给人以圆满而匀称的美感享受．对称之美，首先是和谐之美，正如科学家外尔所说：“对称是一种思想，通过它，人们希望借助它来解释和创造秩序、美和完善．”左图是法国欧普艺术杰出的代表人物瓦萨雷利（1908—1997）的作品，他利用节奏丰富的网格和对称变化的构成，在渐变构架的区域中，塑造立体造型．
知能概述
如图，图形F1的每一点关于直线l的对称点组成的图形F2称为F1关于直线l的轴对称图形．把一个图形变为关于直线l的轴对称图形的变换，叫对称变换．
对称变换前后的对应线段相等，对应角相等，对称轴垂直平分对应点连接的线段．
恰当运用对称变换可实现条件的相对集中．
问题解决
例1如图，∠MON＝50°，点P为∠MON内一定点，点A为OM上一点，点B为ON上一点，当△PAB的周长取最小值时，∠APB 的度数为________．
（湖北省黄冈市竞赛题）
解题思路 运用对称变换，化折为直．
对称是一个广阔的主题，在艺术和自然界中意义重大．数学是它的根本，并且很难找到可以论证数学智慧作用的更好的主题．
——外尔
纸片的折叠
2003年11月在上海召开的第二次“数学开放题及其教学”国际学术研讨会上，日本学者桥本吉彦先生以一张正方形纸片的简单折叠提出以下问题：
如图①、②，一张正方形纸片ABCD，将B折至AD的中点，FG为折痕，将C折至AD的中点，ML为折痕，你能得到哪些结论？
例2 如图，是某台球桌面所示的长方形，小球从A沿45°角击出，恰好经过5次碰撞到B处，则AB∶BC＝（ ）．
A 1∶2 B2∶3 C2∶5 D3∶5
（重庆市竞赛题）
解题思路 台球撞击的实质是对称变换．
例3 如图，已知平面直角坐标系中，A，B两点的坐标分别为A（2，－3），B（4，－1）．
（1）若P（x，0）是x轴上的一个动点，当△PAB的周长最短时，求x的值；
（2）若C（a，0），D（a＋3，0）是x轴上的两个动点，当四边形ABDC的周长最短时，求a的值；
（3）设M，N分别为x轴、y轴上的动点，问：是否存在这样的点M（m，0）和（0，n），使四边形ABMN的周长最短？若存在，求出m，n的值；若不存在，请说明理由．
解题思路 AB，CD的长都为定值，于是只要求PA＋PB最短或AD＋BC最短或MB＋MN＋NA最短，运用轴对称性质化折线为直线．
例4 将正方形ABCD折叠，使顶点A与CD边上的点M重合，折痕交AD于点E，交BC于点F，边AB折叠后与BC交于点G．
（1）如果M为CD边的中点，求证：DE∶DM∶EM＝3∶4∶5；
（2）如果M为CD边上的任意一点，设AB＝2a，问△CMG的周长是否与点M的位置有关？若有关，请把△CMG的周长用含CM的长x的代数式表示；若无关，请说明理由．
解题思路 折痕EF两旁部分图形是关于EF成对称的．对于（2），通过相似三角形性质，把△CMG的周长用相关代数式表示，解题的关键是几何问题代数化．
例3是以下列问题为基础的．
海伦是古希腊亚历山大里亚城精通数学、物理的学者，一天，一位将军向他请教一个问题：
（1）如图①，从A地出发，到笔直的河岸l去饮马，然后再去B地，走什么样的路线最短呢？
（2）如图②，从A地出发，然后沿着笔直的河边走固定的距离a，最后回到B地，怎样选择饮马点，才能使所走路程最短？
折叠问题可从对称观点认识：
（1）折痕两边是全等的；
（2）对应点连线被折痕垂直平分．
解折叠问题常用到勾股定理、相似形、方程等知识及方法．
例5 如图，在△ABC中，AB＝AC，∠BAC＝80°，O为三角形内一点，∠OBC＝10°，∠OCB＝30°，求∠BAO的度数．
（天津市竞赛题）
解题思路 条件与结论并无直接联系．若想到等腰三角形是轴对称图形，作出其对称轴，则能降低问题难度．
例6 如图，求出图中∠DCA的度数．
（日本算术奥林匹克竞赛题）
分析与解 已知角的度数都是12的倍数，36°＋24°＝60°，这使我们想到构造正三角形．
如图，作△ACD关于AD所在直线的轴对称图形△APD，则∠APD＝∠ACD，∠PAD＝∠CAD＝12°，∠PAB＝60°，AP＝AB＝AC，连接PB，则△PAB为正三角形，得∠PBD＝12°．
∵∠DAB＝12°＋36°＝48°＝∠DBA，
∴AD＝BD，
∴△PAD≌△PBD，故∠APD＝∠BPD＝30°，
∴∠ACD＝∠APD＝30°．
例7 如图，在△ABC区域内，小羊从路边AB某点出发跑到水沟边AC喝水，然后跑向路边BC吃草，再跑回到出发点处休息，为使所跑总路程最短，小羊从AB边上的哪一点出发，又按怎样的路线奔跑？
分析与解 （1）如图①，不妨先固定一个点P1，将问题转化为“双动点模型”下的最短路程
（2）改变该定点的位置到P2，仍利用“双动点模型”确定最短路程
（3）比较
与
的长短；
（4）问题转化为比较等腰三角形
与
底边的长短；
在解几何有关问题时，若图形是轴对称图形，则常作出其对称轴；若图形不是轴对称图形，则可选择某直线为对称轴，补为轴对称图形．
对于例6，图形的结构就是作△ACD关于AD所在直线的轴对称图形△APD，又作△APD关于PD所在直线的轴对称图形△BPD，解题就是围绕实现这两次轴对称进行的．
从单动点、双动点到多动点，化动为静，化繁为简．例7展示了转化与化归的思想方法，揭示了这类问题的本质联系．
（5）发现不变量——等腰三角形的顶点（均等于∠ACB的2倍），从而转化为比较两个等腰三角形的腰CP1与CP2的大小；
（6）由于P点是BC边上的动点，问题转化为求CP的最小值；
（7）从而确定P点为BC边上的高线所在的垂足．如图②，这就是小羊的奔跑路线．
台球桌上的数学
台球桌的形状是一个长方形，当母球被击打后可能在不同的边上反弹，为了使母球最终击中目标球，击球者需作出不同的设计，确定击球方向．因此，台球既复杂又有趣，台球运动成为智慧和技能的较量．
例8 （1）如图①，在长方形球台ABCD上，现在要击打P球，使它依次碰撞球台的AB边、BC边、CD边、AD边后，恰好撞到Q球，求P球打击的路线．
（2）如图②，当母球P在AB边中（不包括点A，B），先撞击BC边，反射到CD边，再反射到AD边，最后回到出发点．问母球P的初始路线应该满足什么条件？
图③揭示了台球运动的基本原理，其实质是对称变换．
1．在直角坐标系中，已知A（1，1），B（－1，2），点C在直线y＝－x上，则△ABC 的周长最小为________．
（世界数学团体锦标赛试题）
2．如图，在菱形ABCD中，∠DAB＝60°，AB＝1，点E在边AB上，使得AE∶EB＝2∶1，P为对角线AC上的动点，则PE＋PB的最小值为________．
（“新知杯”竞赛题）
（第2题）
（第3题）
3．如图，在矩形ABCD中，AB＝12，AD＝3，E，F分别是AB，DC上的点，则折线AFEC 长的最小值为________．
（四川省竞赛题）
对称是客观存在，对称是一个数学概念，对称是一种美的标准，对称是一种思维方法．
人们在漫长的岁月里，体验着对称，享受着对称．
4．如图，∠AOB＝30°，M是OA的中点，若BA＋BM＝6，则OA的最大值为________．
（世界数学团体锦标赛试题）
（第4题）
（第5题）
（第6题）
5．如图，在△ABC中，已知∠A＝60°，∠C＝75°，AB＝10，点D，E，F分别在边AB，BC，CA上．则△DEF 周长的最小值为________．
（全国初中数学联赛题）
6．如图，在△ABC中，D是AC边上的中点，连接BD，把△BDC沿BD翻折，得到△BDC′，DC′与AB交于点E，连接AC′．若AD＝AC′＝2，BD＝3，则点D到BC′的距离为（ ）．
（重庆市中考题）
7．如图，在矩形ABCD中，AB＝10，BC＝5，若点M，N分别是线段AC，AB上的两个动点，则BM＋MN的最小值为（ ）．
（黑龙江省中考题）
（第7题）
（第8题）
（第9题）
8．如图，在正方形ABCD中，点E，F将对角线三等分，且AC＝12，点P在正方形的边上，且满足PE＋PF＝9的点P的个数是（ ）．
A．0 B．4 C．6 D．8
（安徽省中考题）
9．如图，在矩形ABCD中，已知对角线长为2，且∠1＝∠2＝∠3＝∠4，则四边形EFGH的周长为（ ）．
（四川省竞赛题）
10．在直角坐标系中，设A（－1，－2），B（4，－1），C（m，0），D（n，n）为四边形的四个顶点．当四边形ABCD的周长最短时，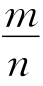
的值为（ ）．
（北京市竞赛题）
11．如图，在△ABC中，AD⊥BC于D，已知∠ABC＞∠ACB，P是AD上的任一点．求证：AC＋BP＜AB＋PC．
（“祖冲之杯”竞赛题）
（第11题）
（第12题）
12．如图，在边长为
的等边△ABC中，M是边BC的中点，P是AC上的点．
（1）当PC为何值时，BP＋PM有最小值？
（2）求出BP＋PM的最小值．
（“宗沪杯”竞赛题）
13．如图①，矩形MNPQ中，点E，F，G，H分别在NP，PQ，QM，MN上，若∠1＝∠2＝∠3＝∠4，则称四边形EFGH为矩形MNPQ的反射四边形，在图②、图③、图④中，四边形ABCD为矩形，且AB＝4，BC＝8．
理解与作图：
（1）在图②、图③中，点E，F分别在BC，CD边上，试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH．
（第13题）
计算与猜想：
（2）求图②、图③中反射四边形EFGH的周长，并猜想矩形ABCD的反射四边形的周长是否为定值？
启发与证明：
（3）如图④，为了证明上述猜想，小华同学尝试延长GF交BC的延长线于M，试利用小华同学给我们的启发证明（2）中的猜想．
（湖北省咸宁市中考题）
14．如图，一个台球桌是直角三角形，如果从斜边上某点朝着垂直于斜边的方向击出台球，那么球在其他两个直角边上反弹后，又能回到斜边上，请证明：台球滚过的距离长与击球点的位置无关（台球反射时服从入射角等于反射角的规律）．
（俄罗斯萨温市竞赛题）
（第14题）
（第15题）
（第16题）
15．如图，在△ABC中，∠ABC＝45°，点D在边BC上，∠ADC＝60°，且BD＝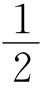
CD，将△ACD以直线AD为轴作轴对称变换，得到△AC′D，连接BC′．
（1）求证：BC′⊥BC；
（2）求∠C的大小．(www.xing528.com)
（天津市竞赛题）
16．如图，在△ABC中，已知∠ABC＝∠BAC＝70°，P为三角形内一点，∠PAB＝40°，∠PBA＝20°．求证：PA＋PB＝PC．
（北京市竞赛题）
折纸中的数学发现
折纸活动过程是一个充满着想象力、创造力和手脑并用的过程．通过折纸活动，观察折痕所形成的边角关系，可以帮助我们建立折纸操作与数学内容的联系．
数学寓于折纸之中，从折痕中能发现大量的几何对象和性质，如全等、对称、相似、比例等，因此，折纸已成为现代几何学的一个分支．
17．动手操作：
如图①，四边形ABCD是一张正方形纸片，先将正方形ABCD对折，使BC与AD重合，折痕为EF，把这个正方形展平，然后沿直线CG折叠，使B点落在EF上，对应点为B′．
数学思考：
（1）求∠CB′F的度数；
（2）如图②，在图①的基础上，连接AB′，试判断∠B′AE与∠GCB′的大小关系，并说明理由．
从数学的角度去研究折纸，从数学教学的视角去开发折纸．
折纸数学，所有从事这一领域研究的科学家几乎一开始都只是被折纸过程所蕴含的简单而纯粹的美所吸引，但他们的工作开启了一个科学和工程学的宝库．
（第17题）
解决问题：
（3）如图③，按以下步骤进行操作：
第一步 先将正方形ABCD对折，使BC与AD重合，折痕为EF，把这个正方形展平，然后继续对折，使AB与DC重合，折痕为MN，再把这个正方形展平，设EF和MN相交于点O；
第二步 沿直线CG折叠，使B点落在EF上，对应点为B′；再沿直线AH折叠，使D点落在EF上，对应点为D′；
第三步 设CG，AH分别与MN相交于点P，Q，连接B′P，PD′，D′Q，QB′．
试判断四边形B′PD′Q的形状，并证明你的结论．
（山西省中考题）
18．我们知道，A4，B5复印纸是彼此相似的长方形，它们的长宽比是
，我们称这样的长方形为
长方形．对于一张正方形的纸，仅使用折叠的方式就可以将它折成
长方形的形状，步骤如下：
（第18题）
第一步 折叠正方形ABCD，使其对角线BD为折痕；
第二步 折起∠C，折叠后将BC与BD重合，折痕为BH，点C关于BH的对称点为G；
第三步 折叠出过点G的折痕EF，使EF∥AD．
如图所示，则长方形BCFE为
长方形．
（1）请对上面得到的结论给出证明；
（2）请在正方形纸上折叠出
长方形，并叙述折叠的步骤和证明．
（北京市数学知识应用竞赛试题）
19．如图，从A点射入m×4的网格图中的一束光线，只要射到边AB，BC，CD，AD上，就发生反射，在遇到点A，B，C或D时从该点射出．若从A点射入的光线在经过2016个格点后从格点D射出（包括点A，D，重复经过的格点只计算一次），求m．
（第19题）
（世界数学团体锦标赛试题）
例1 80° 如图，∠CPD＝360°－90°－90°－50°＝130°，∠P′＋∠P″＝50°，从而∠P′PA＋∠P″PB＝50°，
∴∠APB＝130°－50°＝80°．
例2 C 如图，作A点关于BC的对称点A′，B关于AD的对称点B′，设CD的中点为M，作M点关于AD的对称点M′，关于BC的对称点M″，连接A′M′，交AD，BC于G，H，连接B′M″，交AD，BC于E，F．小球路线为A→H→G→M→F→E→B，AE＝EG＝2GD＝CD，AB∶BC＝2∶5．
（例1）
（例2）
（例5）
例8 （1）作法：
①作点P关于AB的对称点P1，再作点P1关于BC的对称点P2；
②作点Q关于AD的对称点Q1，再作点Q1关于DC的对称点Q2；
③连接P2Q2，分别交BC，CD于F，G，连接FP1交AB于点E，GQ1交AD于点H．折线PEFGHQ即为所求的路线．
需要指出的是，上面求得的路线，恰好也是一条最短路线．
（2）只要出发的线路是平行于台球桌的对角线的就一定能回到出发点．
（例8）
1．
作点A关于直线y＝－x的对称点A′（－1，1），当C落在A′B上时，BC＋CA的长最小．
2．
B，D关于AC对称，连接DE交AC于P，则PE＋PB＝DE的值最小．
3．15 如图，分别作A，C关于DC，AB的对称点A1，C1，连接A1C1分别交AB，DC于点E1，F1．连接A1F，C1E，过A1作BC延长线的垂线，G为垂足．又A1G＝AB＝12，C1G＝3AD＝9，则
＝15，故AF＋FE＋EC＝A1F＋FE＋EC1≥A1C1＝15．当点E，F分别与E1，F1重合时，取到最小值15．
（第3题）
（第4题）
（第5题）
（第7题）
7．B 作点B关于AC对称点B′，连接MB′，则BM＋MN＝B′M＋MN．当M，B′，N三点不共线时，B′M＋MN大于当M，B′，N三点共线时B′M＋MN的值；当M，B′，N三点共线，且B′N⊥AB时，B′M＋MN有最小值，如图，可得
8．D 作点F关于AB的对称点G，连接EG交AB于点P，此时PE＋PF的值最小，最小值 ＝
；而点P与点A重合时，PE＋PF＝4＋8＝12＞9；点P与点B重合时，PE＋PF＝
．故在AB上满足条件的点有2个；同理，在BC，CD，DA上满足条件的点P分别有2个．
9．B 根据反射关系，可作出如图所示的图形，则Rt△IJK的斜边就是四边形EFGH的周长，也可用特殊位置法验证．
10．A
（第9题）
11．以AD为对称轴，将△ABD翻折，B点落在CD上，设为点B′，连接P′B，AB′，设AB′与PC交于点E．
12．（1）如图，连接AM，把△ABC沿AC轴翻转180°得到△ADC，N是M的对称点（关于AC对称）．
此时，总有PM＝PN．
由于B，N是定点，故BP＋PN≥BN，等号成立条件是：当且仅当点P在边BN上．
以下求PC的值．
（第12题）
延长BC到E，使CE＝CN，得等边△CEN．由作法可知PC∥NE，
，即
故当PC＝＝
时，BP＋PM有最小值．
（2）过点N作NF⊥CE，F为垂足，则
BN＝
＝7，故BP＋PM的最小值为7．
13．（1）略
（2）图②、图③中反射四边形EFGH的周长为
．猜想：矩形ABCD的反射四边形的周长为定值．
（3）延长GH交CB的延长线于N，可证明NH＝EH，NB＝EB，EF＝MF，EC＝MC，GM＝GN，四边形EFGH的周长为
14．把Rt△ABC的斜边AB作为直线l，以直角边BC及AC为对称轴，作两条与l对称的直线l′和l″，它们相互平行，如图所示．当台球从M点处击出后，它的轨迹MNKL就相当于在对称变换后的线段M′L′，它垂直于直线l′及l″．由于这两条平行线上所有的点都和另一条直线上的点等距离，所以台球经过的路径就将与起点无关了．
15．（1）C′D＝CD，BD＝
C′D，∠BDC′＝60°，取C′D中点P，连BP，则△BDP为等边三角形，∠BC′D＝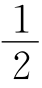
∠BPD＝30°，于是∠C′BD＝90°，即BC′⊥BC．
（第14题）
（2）如图，过点A分别作BC，C′D，BC′的垂线，E，F，G为垂足，则AE＝AF，AE＝AG，AG＝AF．
∴点A在∠GC′D的角平分线上．
∵∠BC′D＝30°，∴∠GC′D＝150°，∠AC′D＝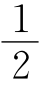
∠GC′D＝75°，
故∠C＝∠AC′D＝75°．
（第15题）
（第16题）
16．因为∠ABC＝∠BAC＝70°，所以，AC＝BC，∠ACB＝40°．
如图，在BP延长线上取一点N，使PN＝PA，连接AN，CN．易知，∠APB＝120°，则∠APN＝60°．
因此，△APN是等边三角形．
由∠PAC＝30°＝∠NAC，知AC为PN的垂直平分线，则NC＝PC，∠NCA＝∠PCA．
将△CAN逆时针旋转到△CBM的位置，则∠NCM＝∠ACB＝40°．
作CH⊥AB于点H，交PM于点K，由PC＝MC，得CH⊥PM．
因此，PM∥AB．
由∠MBC＝∠NAC＝30°，∠MBA＝40°，得∠MBP＝20°＝∠MPB．从而，PM＝BM＝PN．
则△NCP≌△MCP，⇒∠MCP＝∠NCP．故∠NCA＝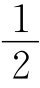
∠NCP＝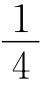
∠NCM＝10°．
于是∠NCB＝∠NCA＋∠ACB＝∠NBC，因此NB＝NC．
故PC＝NC＝NB＝NP＋PB＝PA＋PB．
17．（1）∠CB′F＝30°．
（2）∠B′AE＝∠GCB′＝15°．
（3）四边形B′PD′Q为正方形．
如图，连接AB′，由（2）知，∠B′AE＝∠GCB′．
由折叠知，∠GCB′＝∠PCN，∴∠B′AE＝∠PCN．
由对折知，∠AEB′＝∠CNP＝90°，AE＝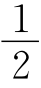
AB，CN＝
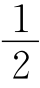BC．
（第17题）
又∵四边形ABCD是正方形，∴AB＝BC，AE＝CN，∴△AEB′≌△CNP，∴EB′＝NP．
同理可得，FD′＝MQ，由对称性可知，EB′＝FD′，∴EB′＝NP＝FD′＝MQ．
由两次对折可知，OE＝ON＝OF＝OM，
∴OB′＝OP＝OD′＝OQ，∴四边形B′PD′Q为矩形．
由对折知MN⊥EF于点O，∴PQ⊥B′D′于点O．
∴四边形B′PD′Q为正方形．
18．（1）过点G作BC边的垂线，与BC相交于点M（图①）．由折纸的第三步可知，折痕EF∥BC，从而四边形BMGE构成一个正方形，且有BG∶
∶1．由折纸的第二步可知BG＝BC．因此长方形BCFE的长宽比为BC∶BE＝BG∶
∶1．从而它是个
长方形．
（第18题）
（2）折叠
长方形，如图②．
第一步，将正方形ABCD的两对边AB与CD重合对折，折痕为EF；
第二步，过点B将点C折到EF上，折痕为BG，点C关于BC的对称点为H；
第三步，延长BH交AD于点M，折叠出过点M的折痕MN，使MN∥AB．
则四边形ABNM为
长方形．
证明：显然△BCH是正三角形，HF是这个三角形的高，故
又△BFH∽△BNM，所以
19．如图，由光线在网格图中反射的规律，可知光线只可能经过BC边上的点B，C或BC的中点G，由题意可知，当光线经过点B或C时，从该点射出，不符合题意，所以光线在G点发生反射．
观察图中光线经过的格点的规律可知，这些格点分别在AB，CD或EG上，且数量相等，由光线经过2016个格点可知，光线经过边AB上的格点数是2016÷3＝672，m＝672×2－1＝1343．
（第19题）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
