图形面积计算与应用，精英数学大视野

自然界的对称之美，曾使无数人为之倾倒．然而，科学家李政道和杨振宁却提出了基本粒子在弱相互作用条件下的宇称不守恒定律．

著名画家吴冠中的水墨画《对称乎，未必，且看柳与影》形象地显现了物理学理论关于自然界对称与不对称原则的深刻含义．

知能概述

几何学发端于测量土地的面积．面积是几何学研究的一个重要内容，运用公式、等积变换、面积比定理是计算面积的基本方法．

面积也是研究几何学的有力工具，借助于面积相关知识解决一些题目中不涉及面积问题的方法称为面积法．

熟悉下列基本图形、基本结论：

问题解决

例1如图，矩形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，点P在矩形ABCD内，若AB＝4cm，BC＝6cm，AE＝CG＝3cm，BF＝DH＝4cm，四边形AEPH的面积为5cm2，则四边形PFCG的面积为________cm2．

（浙江省竞赛题）

物理的日趋数学化意味着在我们的领域内这最后一种美越来越重要．

——杨振宁

海伦公式

海伦，古希腊数学家，找到了给出三角形三边a，b，c，求三角形面积的公式：S＝其中

我国宋代著名数学家秦九韶在《数书九章》中给出了与海伦公式等价的公式：

解题思路　把不规则四边形PFCG的面积表示为规则图形面积的和差．

例2　如图，在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD＝4，CE＝6，那么△ABC的面积等于（　）．

A．12　B．14

C．16　D．18

（全国初中数学联赛题）

解题思路　由中点想到三角形中位线，△ABC与四边形BEDC面积存在一定的关系．

例3　已知一个三角形的三边长分别为，求此三角形面积．

（“希望杯”邀请赛试题）

解题思路　直接运用海伦公式、勾股定理，借助三角形面积公式，运用的几何意义可使问题获得简解．

例4　如图，四边形PQMN是ABCD的内接四边形．

（1）若MP∥BC或NQ∥AB，求证：S四边形PQMN＝S▱ABCD；

（2）若S四边形PQMN＝S▱ABCD，问是否能推出MP∥BC或QN∥AB？证明你的结论．

（“宇振杯”上海市竞赛题）

如图，若四边形对角线d1，d2夹角为α，则其面积

特别地，当d1⊥d2时，则S＝d1d2．

有些几何问题，虽然题目中没有直接涉及面积，但由于面积关联着边、角两个重要元素，所以我们可从面积角度思考问题，这就是常说的面积法．

用面积法解题的基本步骤是：

（1）用不同方法或从不同角度计算某一图形面积，得到一个含边或含角的关系式；

（2）化简这个面积关系式，直至得到求解或求证的结果．

当问题涉及三角形的高、垂线或角平分线时，不妨用面积法试一试．

解题思路　由平行的条件或证明两直线平行，从等积定理入手．

例5　如图，设凸四边形ABCD的一组对边AB，CD的中点分别为K，M．求证：S四边形ABCD＝S△ABM＋S△CDK．

（俄罗斯莫斯科市竞赛题）

解题思路　S四边形ABCD＝S△ABM＋S△ADM＋S△BMC，只需证明S△CDK＝S△ADM＋S△BCM，这三个三角形底有联系，寻找高之间的关系是证题的关键．

（河北省竞赛题）

秦九韶（约1208－约1261）的代表作是《数书九章》，他对“大衍求一术”和“正负开方术”的研究，取得了卓越的成果，美国科学史家萨顿说：“秦九韶是他那个民族、他那个时代，并且确实也是所有时代最伟大的数学家之一．”

线段比与面积比的相互转化，是解面积问题的常用技巧．转化的基本知识有：

（1）等高三角形面积比，等于它们的底之比；

（2）等底三角形面积比，等于它们的高之比；

（3）相似三角形面积比，等于它们相似比的平方．

面积平分

例8　请你画出一条直线，将如图所示的图形分割成面积相等的两部分．

解题思路　从特殊情形看，通过割补把一个不规则图形化归为若干规则图形的组合；或居高临下建立直角坐标系，直观领悟这样的直线有几条、怎样画出这些直线．

在例7的基础上，我们可以进一步证明：

（1）＝2；

（2）中，至少有一个不大于2，也至少有一个不小于2．

三角形中一个点，简单的图形蕴含丰富的问题．在数学家眼中，一个基本图形犹如手中的万花筒，稍一转动，就生成美丽的图案，但拆开，只是几个涂有颜色的碎片．

1．如图，已知凸四边形ABCD的面积是a，E，F，G，H分别是AB，BC，CD，DA的中点，那么图中阴影部分的总面积是________．

（江苏省竞赛题）

2．如图，∠ADC＝30°，△ABC为正三角形，若AD＝3，BD＝5，则△ACD的面积是________．

（“希望杯”邀请赛试题）

（第1题）

（第2题）

（第3题）

3．如图，设D是△ABC的边AB上的一点，作DE∥BC交AC于点E，作DF∥AC交BC于F，已知△ADE，△DBF的面积分别为m和n，则四边形DECF 的面积为________．

（全国初中数学联赛题）

4．如图，设D，E，F分别为△ABC的边BC，CA，AB上的点，且＝1，，S△ABC＝24，则△DEF 的面积为________．

（浙江省竞赛题）

（第4题）

（第5题）

（第6题）

5．如图，正方形纸片ABCD中，E为BC的中点，折叠正方形使点A与点E重合，压平后折痕为MN．则梯形ADMN与梯形BCMN的面积之比为________．

（四川省竞赛题）

6．如图，在直角坐标系xOy中，已知点O（0，0），A（8，0），B（6，4），C（1，2），点P在OA上，直线PB平分四边形OABC的面积，则直线PB的解析式为________．

（“希望杯”邀请赛试题）

7．如图，已知P是ABCD内一点，且S△PAB＝5，S△PAD＝2，则S△PAC等于（　）．

A．2　B．3　C．3．5　D．4

（湖北省黄冈市竞赛题）

（第7题）

（第9题）

（第10题）

8．已知菱形ABCD的两条对角线AC，BD的乘积等于菱形的一条边长的平方，则菱形的一个钝角的大小是（　）．

A．165°　B．135°　C．150°　D．120°

（“希望杯”邀请赛试题）

9．如图，是一个由5张纸拼接成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形的面积为S3，则这个平行四边形面积一定可以表示为（　）．

A．4S1　B．4S2　C．4S2＋S3　D．3S1＋4S3

（浙江省宁波市中考题）

10．如图，在凸四边形ABCD中，E，F分别为边AB，CD的中点，AF，DE交于点G，BF，CE交于点H．四边形EGFH的面积为10，则△ADG与△BCH的面积和为（　）．

A．　B．10　C．15　D．20

（四川省竞赛题）

11．已知一个正八边形中最长的对角线等于a，最短的对角线等于b，则这个正八边形的面积等于（　）．

A．a2＋b2　B．a2－b2　C．a＋b　D．ab(www.xing528.com)

（北京市竞赛题）

12．如图，点D，E分别在△ABC的边AC，AB上，BD与CE交于点O，△OBE，△OBC，△OCD的面积分别为15，30，24．则AE∶BE＝（　）．

A．5∶2　B．2∶1

C．5∶4　D．9∶5

（第12题）

（全国初中数学邀请赛试题）

13．问题探究：

（1）请在图①中作出两条直线，使它们将圆面四等分．

（2）如图②，M是正方形ABCD内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M），使它们将正方形ABCD的面积四等分，并说明理由．

问题解决：

（3）如图③，在四边形ABCD中，AB∥CD，AB＋CD＝BC，点P是AD的中点，如果AB＝a，CD＝b，且b＞a，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？若存在，求出BQ的长；若不存在，说明理由．

（陕西省中考题）

（第13题）

（第14题）

14．如图，已知三角形ABC的面积为120，AB＝50，AC＝10，D，E分别是AB，AC的中点，∠BAC的平分线分别交DE，BC于点F，G，求四边形FDBG的面积．

（美国数学竞赛题）

15．如图，在凸五边形ABCDE中，已知AB∥CE，BC∥AD，BE∥CD，DE∥AC，求证：AE∥BD．

（加拿大数学奥林匹克试题）

（第15题）

（第16题）

（第17题）

16．如图，在锐角△ABC中，D，E，F分别是AB，BC，CA边上的三等分点，P，Q，R分别是△ADF，△BDE，△CEF的三条中线的交点．

（1）求△DEF与△ABC的面积比；

（2）求△PDF与△ADF的面积比；

（3）求多边形PDQERF与△ABC的面积比．

（“希望杯”邀请赛试题）

17．如图，依次延长四边形ABCD的边AB，BC，CD，DA至E，F，G，H，使＝m．若S四边形EFGH＝2S四边形ABCD，求m的值．

（上海市竞赛题）

梅涅劳斯定理和塞瓦定理是平面几何中的两个著名定理，前者可证明共线点问题，后者可证明共点线问题．两个定理证法较多，但面积法尤为独特简练．

18．如图，一直线截△ABC的边AB，AC及BC的延长线分别交于F，E，D三点，求证：＝1．（梅涅劳斯定理）

（第18题）

（第19题）

（第20题）

19．如图，在△ABC中，已知，求的值．

（“华罗庚金杯”少年数学邀请赛试题）

20．如图，以Rt△ABC（∠ACB＝90°）的三边CA，CB，AB向外分别作正方形CADE，正方形BCFG，正方形ABHI．记边CB，CA的长分别为a，b，凸六边形DEFGHI的面积为S．问：是否存在正整数a，b，使得S＝2016？若存在，求出所有的正整数a，b；若不存在，说明理由．

（四川省竞赛题）

例5　过A，K，B分别作CD的垂线，它们的长分别记作h1，h2，h3．

（例5）

例8　这样的直线有无数条，画法如下：

（1）设直线PQ被原图形截得的线段的中点为O；

（2）过点O任作一条直线MN（只要MN与AB，CD两边都有交点）都能把原图形分成面积相等的两部分．

（例8）

（第2题）

（第4题）

7．B　8．C　用面积法解．　9．A

10．B　特殊化，由AB∥CD，得S△ADG＝S△EGF，S△BHC＝S△EHF，故SADG＋SBHC＝SEGF＋SEHF＝S四边形EGFH＝10．

（第6题）

11．D　如图，正八边形ABCDEFGH中，最长的对角线AE＝BF＝CG＝DH＝a，最短的对角线AC＝BD＝CE＝DF＝EG＝FH＝GA＝HB＝b．进行割补，如图所示，可得S八边形ABCDEFGH＝SPQMN＝ab．

12．B　连接OA，设S△AOE＝x，S△AOD＝y，将面积比转化为线段比，建立关于x，y的方程组．

13．（1）如图①所示．

（2）如图②所示，证明略．

（第11题）

（第13题）

（3）存在．当BQ＝CD＝b时，PQ将四边形ABCD面积二等分．

理由如下：如图③，延长BA到点E，使AE＝b，延长CD到点F，使DF＝a，连接EF．

∵BE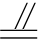CF，BE＝BC＝a＋b，

∴四边形EBCF是菱形．

连接BF交AD于点M，则△MAB≌△MDF，

∴AM＝DM，

∴P，M两点重合，

∴P点是菱形EBCF对角线的交点．

在BC上截取BQ＝CD＝b，则CQ＝AB＝a，设点P到菱形EBCF一边的距离为d，

20．如图，延长BA至点B′，使得B′A＝AB，连接B′C．

易证△B′AC≌△IAD．

则S△IAD＝S△B′AC＝S△ABC．

类似的，S△ECF＝S△ABC＝S△HBG．

故

（第20题）

＝2（a2＋b2＋ab）．

假设存在正整数a，b，使得S＝2016，即a2＋b2＋ab＝24×32×7．　①

易知，a，b均为偶数（否则，若a，b均为奇数或一奇一偶，得a2＋ab＋b2均为奇数，矛盾）．

令a＝2a1，b＝2b1．代入式①得

＋＋a1b1＝22×32×7．

类似的，a1，b1均为偶数．

令a1＝2x，b1＝2y．

从而，x2＋y2＋xy＝32×7．　②

不妨设x≤y，则32×7≥3x2．故x2≤21．

注意到，x，y为正整数，则x＝1，2，3，4．

代入式②，经检验，只有当x＝3时，

y2＋3y＝54⇒y＝6或－9（舍去）．

故（x，y）＝（3，6），（6，3）

⇒（a，b）＝（12，24），（24，12）．