八年级2020数学教材：第25讲几何不等式

艺术诠释了数学的内涵，使数学变得通俗易懂；数学开拓了艺术的内涵，使艺术变得意味深长．

计算机是一种工具，它把枯燥的数学公式翻译成能看得见的模式．左图是编程者和算法艺术家为研究波浪运动编写程序产生的线型图像．

知能概述

几何不等式是指平面图形中所含的线段长度、角的大小、周长、面积等所呈现出的不等关系．

解几何不等式问题，常用到下列基本知识：

（1）两点之间线段最短；

（2）垂线段最短；

（3）三角形三边关系，三角形内角、外角关系定理；

（4）同一个三角形中，大边对大角，小边对小角，反之亦然；

（5）在两边对应相等的两个三角形中，第三边大的所对的角也大，反之亦然．

问题解决

例1　（1）如图，在Rt△ABC中，∠B＝90°，AB＝4，BC＞AB，点D在BC上，以AC为对角线的所有平行四边形ADCE中，DE 的最小值是________．

（山东省东营市中考题）

（2）锐角三角形ABC中，AB＞BC＞AC，且最大内角比最小内角大24°，则∠A 的取值范围是________．

（江苏省竞赛题）

解题思路　对于（1），DE＝2DO，将问题转化为求OD的最小值，而O为定点．

对于（2）由AB＞BC＞AC，得∠C＞∠A＞∠B，设∠B＝x，把∠C，∠A用x的代数式表示，并建立关于x的不等式组．

我的许多工作是根据数学原理来做的，我发现无论从艺术的角度还是从设计理念的角度看，数学图形都是丰富的源泉．

——勃列森

厄尔多斯-莫代尔不等式

如图，P为△ABC内任一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，则PA＋PB＋PC≥2（PD＋PE＋PF）．

例2　如图，在△ABC中，∠BAC＝120°，点P是△ABC内一点，则（　）．

A．PA＋PB＋PC＜AB＋AC

B．PA＋PB＋PC＞AB＋AC

C．PA＋PB＋PC＝AB＋AC

D．PA＋PB＋PC与AB＋AC的大小关系与点P的位置有关

解题思路　旋转△APC，化折线为直线．

例3　如图，在等腰△ABC的一腰AB上取一点D，在另一腰AC的延长线上截取CE＝BD，连接DE，求证：DE＞BC．

（陕西省西安市竞赛题）

解题思路　平移DE，构造以DE和BC为边的三角形．

例4　如图，在△ABC中，AB＝AC，BC的中点为D，E为△ABD内任意一点，连接AE，BE，CE．求证：∠AEB＞∠AEC．

解题思路　作点E关于AD的对称点E′，连接AE′，E′C，EE′，并延长EE′交AC于F，利用对称性，把角集中到一个易讨论的图形中．

例5　如图，P为边长为1的等边三角形ABC形内任意一点．设l＝PA＋PB＋PC，求证：1．5＜l＜2．

（北京市竞赛题）

解题思路　从三角形三边关系入手，解题的关键是运用不等式性质，对于证明l＜2，需构造等边三角形．

例6　设△ABC中内角A，B，C所对的边分别为a，b，c，面积为S，求证：

（1）3（a2＋b2＋c2）≥（a＋b＋c）2；

（2）（a＋b＋c）2≥

（3）a2＋b2＋c2≥

解题思路　三角形的边长与面积之间有相等关系，也有不等关系，充分运用作差、基本不等式、放缩等代数技巧方法，是证明的关键．

把欲证的不等量尽可能集中到一个三角形（或两个具有紧密关系的三角形）中，以便运用三角形不等关系的性质，这是解几何不等式问题的常用思路，为此需用到几何变换．

几何不等式将几何的论证与不等式的技巧有机地结合在一起，简单而不平凡，优美而不单调．

费马点

人类每天为解决最值问题而忙碌着，大自然亦是如此．最早指出自然界中到处都潜藏着最值问题的人，大概是费马．

在已知△ABC所在平面上求一点F，使它到三角形三顶点的距离之和为最小．

这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的．这个问题中所求的点被人们称为“费马点”．

例7　如图，设F是锐角△ABC内一点，使∠AFB＝∠BFC＝∠CFA＝120°，而P是△ABC内任意一点，求证：PA＋PB＋PC≥FA＋FB＋FC．

证明　将△ABF，△ABP绕B点依逆时针方向旋转60°，得到△A′BF′和△A′BP′，连接FF′，PP′，由旋转的性质得△BPP′与△BFF′都是正三角形，故FF′＝FB，PP′＝PB．

又△A′BF′≌△ABF，

∴∠A′F′B＝∠AFB＝120°．

∵∠FF′B＝60°，∴A′，F′，F三点共线．

同理，由∠F′FB＝60°以及∠BFC＝120°知C，F，F′也三点共线．从而，C，F，F′，A′四点共线．

类似的，由旋转的性质知△A′P′B≌△APB，

∴∠A′P′B＝∠APB＝120°．

又∠BP′P＝60°，∴A′，P′，P三点共线．

∵A′C是直线段，而A′P与PC是折线段，

∴A′P＋PC≥AC′，即A′P′＋P′P＋PC≥A′F′＋F′F＋FC，

注意到A′P′＝PA，P′P＝PB，A′F′＝AF，F′F＝FB，

故有PA＋PB＋PC≥FA＋FB＋FC．

1．△ABC的内角中，∠A为最小，∠B为最大，且2∠B＝5∠A，则∠B的取值范围是________．

（江苏省竞赛题）

2．如图，在△ABC中，AE是∠BAC的外角平分线，D是这条平分线上的任一点，则AB＋AC和BD＋DC之间的大小关系是：AB＋AC________BD＋DC（填“＞”“＝”或“＜”号）．

（第2题）

（浙江省杭州市“求是杯”竞赛题）

（1）如图①，当△ABC三内角均小于120°时，F在△ABC内部，此时，∠AFB＝∠BFC＝∠CFA＝120°．

（2）如图②，当△ABC有一角（不妨设为∠A）≥120°时，F点与A点重合．

费马（1601—1665），他在大学里学的是法律，后来当了律师，却把几乎全部业余时间用于数学研究．费马在17世纪创立的解析几何、概率论和数论等领域，都做出了开创性的贡献，成为17世纪最著名的数学家之一，人称“业余数学家之王”．

3．问题背景：如图①，将△ABC绕点A逆时针旋转60°得到△ADE，DE与BC交于点P，可推出结论：PA＋PC＝PE．

问题解决：如图②，在△MNG中，MN＝6，∠M＝75°，MG＝．点O是△MNG内一点，则点O到△MNG三个顶点的距离和的最小值是________．

（湖北省武汉市中考题）

（第3题）

4．如图，在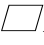ABCD中，AD＝a，CD＝b，过点B分别作边AD，CD上的高ha，hb，已知ha≥a，hb≥b，对角线AC＝20，则S▱ABCD ＝________．

（北京市竞赛题）

（第4题）

（第5题）

（第6题）

5．在Rt△ABC中，∠ABC＝90°，AB＝4，BC＝2，如图，将直角顶点B放在原点，点A放在y轴正半轴上，当点B在x轴上向右移动时，点A也随之在y轴上向下移动，当点A到达原点时，点B停止移动，在移动过程中，点C 到原点的最大距离为________．

6．如图，在Rt△ABC中，AB＝10，∠BAC＝45°，∠BAC的平分线交BC于点D．E，F分别是线段AD和AB上的动点，则BE＋EF的最小值为________．

（山东省日照市中考题）

7．在锐角△ABC中，已知其两边a＝1，b＝3，那么第三边c的变化范围是（　）．

（“祖冲之杯”竞赛题）

8．平面直角坐标系xOy中，已知A（－1，0），B（3，0），C（0，－1）三点，D（1，m）是一个动点，当△ACD的周长最小时，△ABD的面积为（　）．

（江苏省南通市中考题）

9．在△ABC中，∠A，∠B，∠C的对边为a，b，c，已知a2＝b（b＋c），∠C为钝角，则a，2b，c的大小关系是（　）．

A．a＜2b＜c　B．a＜c＜2b

C．2b＜a＜c　D．a＝2b＜c

（湖北省黄冈市竞赛题）

10．如图，在△ABC中，D为BC中点，DM平分∠ADB交AB于点M，DN平分∠ADC交AC于点N，则MN与BM＋CN的关系为（　）．

A．BM＋CN＝MN　B．BM＋CN＜MN

C．BM＋CN＞MN　D．无法确定

（北京大学自主招生试题）

11．如图，在等边△ABC中，BD＝2CD，DE⊥BE，CE，AD相交于点P，则（　）．

A．AP＞AE＞EP　B．AE＞AP＞EP

C．AP＞EP＞AE　D．EP＞AE＞AP

（湖北省武汉市竞赛题）

（第10题）

（第11题）

（第12题）

12．如图，∠MON＝90°，矩形ABCD的顶点A，B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB＝2，BC＝1，在运动过程中，点D到点O的最大距离为（　）．

（山东省济南市中考题）

13．如图，已知正方形ABCD内一动点E到A，B，C三点的距离之和的最小值为，求此正方形的边长．

（广东省竞赛题）

（第13题）

（第14题）

14．如图，设凸四边形ABCD的对角线相交于O，且AC⊥BD，已知OA＞OC，OB＞OD，求证：BC＋AD＞AB＋CD．

（“祖冲之杯”竞赛题）(www.xing528.com)

15．如图，在凸四边形ABCD中，AB是最短的边，CD是最长的边．

求证：∠A＞∠C且∠B＞∠D．

（青少年数学国际城市邀请赛试题）

（第15题）

（第16题）

16．（1）如图①，在四边形ABCD中，BC⊥CD，∠ACD＝∠ADC，求证：AB＋AC＞

（2）如图②，在△ABC中，AB边上的高为CD，试判断（AC＋BC）2与AB2＋4CD2之间的大小关系，并证明你的结论．

（江苏省竞赛题）

17．如图，已知点P是锐角△ABC内的一个点，且使PA＋PB＋PC最小，试确定点P的位置，并证明你的结论．

（天津市竞赛题）

（第17题）

（第18题）

（第19题）

18．如图，在凸四边形ABCD中，若AB＋BD≤AC＋CD，求证：AB＜AC．

（匈牙利数学竞赛题）

19．如图，悬空放置的长方体ABCD－EFGH中，AE＝6，AB＝7，AD＝8，点M是矩形ABFE的中心，点N是线段FG的中点．已知点M，点N处各有一块糖，点D处有一只蚂蚁，问：蚂蚁最少爬多远能找到糖？

（世界数学团体锦标赛试题）

20．证明：任意三角形的三个内角平分线的乘积必小于三边的连乘积．

（上海市竞赛题）

例1　（1）4　当OD⊥BC时，OD的值最小．

（2）52°＜∠A＜68°　∠C＝x＋24°，∠A＝156°－2x，

则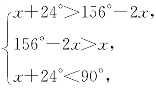解得　44°＜x＜52°，

∴52°＜156°－2x＜68°，即52°＜∠A＜68°．

例2　B

将△APC绕点A逆时针旋转60°得△AP′C′，连接PP′，CC′，则△APC≌△AP′C′，AC′＝AC，PC＝P′C′，PA＝P′A，B，A，C′共线．

∵∠PAP′＝60°，AP＝AP′，

∴△PAP′为正三角形，

∴PA＝P′A＝PP′，

∵PB＋PP′＋P′C′＞AB＋AC′，

∴PA＋PB＋PC＞AB＋AC．

例3　过D作DFBC，连接CF，则CF＝CE，可证明∠DFE＞∠DEF，故DE＞DF＝BC．

例4　△AEB≌△AE′C，∠AEB＝∠AE′C．

∵∠AE′F＝∠AEF＋∠EAE′＞∠AEF，

∠CE′F＝∠CEF＋∠ECE′＞∠CEF，

∴∠AE′F＋∠CE′F＞∠AEF＋∠CEF，

∴∠AE′C＞∠AEC，故∠AEB＞∠AEC．

（例2）

例5　∵AP＋BP＞AB＝1，BP＋CP＞BC＝1，CP＋AP＞AC＝1，

∴相加得2（PA＋PB＋PC）＞3，即l＞1．5．

过P作MN∥BC，交AB于M，交AC于N，则

△AMN是正三角形，MN＝AM，而∠APN＞∠ANP＝60°，

∴PA＜AN．

∵BP＜PM＋MB，PC＜PN＋NC，

∴PA＋PB＋PC＜AN＋PM＋BM＋PN＋NC＝（AN＋NC）＋（PM＋PN）＋BM＝AC＋MN＋BM＝AC＋AM＋BM＝AC＋AB＝2，即l＜2．

故1．5＜l＜2．

例6　（1）∵3（a2＋b2＋c2）－（a＋b＋c）2＝（a－b）2＋（b－c）2＋（c－a）2≥0，

∴3（a2＋b2＋c2）≥（a＋b＋c）2．

（例5）

1．75°≤∠B≤100°

2．＜

（第3题）

8．C　点D在直线x＝1上，点A关于x＝1的对称点为B，连接BC交直线x＝1于点D，此时AD＋CD最小．

9．A　a2＝b（b＋c）＜b（2b＋a），（a－2b）（a＋b）＜0，

∴a＜2b，又∠C为钝角，

∴a2＋b2＜c2，

即b（b＋c）＋b2＜c2，（2b－c）（b＋c）＜0，

∴2b＜c，故a＜2b＜c．

10．C

（第5题）

11．A　BE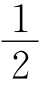＝BD＝DC，则△BEC≌△CDA．∠APE＝∠PAC＋∠ACP＝∠PCD＋∠ACP＝60°．

∠EAP＜60°＝∠APE＜∠PEA，即AP＞AE＞EP．

12．A　取AB中点E，连接OE，DE，则DE≤OE＋DE，当O，E，D三点共线时，等号成立，此时OD长最大．

13．将△ABE绕B点逆时针旋转60°，得△FBG，连接GE，FC，则△BEG为等边三角形，GE＝BE．

∴FC≤FG＋GE＋EC，即FC≤EA＋EB＋EC．

∵FC为定长，

∴当E点落在FC上时，FC＝EA＋EB＋EC为最小值．

∵∠FBC＝150°，FB＝BC，

∴∠BCF＝∠BFC＝15°，而∠GEB＝60°，

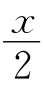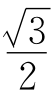∴∠EBC＝45°，即E在正方形ABCD的对角线BD上，作FH⊥BC交CB延长线于点H，设BC＝x，则FB＝x，FH＝ ，HB＝x．

（第13题）

在Rt△FHC中，由得x＝2或x＝－2（舍去），即正方形的边长为2．

14．在OA上截取OC′＝OC，在OB上截取OD′＝OD，连接AD′，BC′，C′D′，交于P点，则AD＝AD′，BC＝BC′，CD＝C′D′．所以BC＋AD＝BC′＋AD′＝BP＋PC′＋AP＋PD′＞AB＋C′D′＝AB＋CD．

15．连接AC，BD，证明略．

16．（1）连接BD，则

（2）（AC＋BC）2≥AB2＋4CD2　如图，作BE⊥AB，使BE＝2CD，连CE，作CF⊥BE，则BF＝CD，CE＝CB．应用（1）的结论，有（AC＋BC）2＞AB2＋BE2＝AB2＋4CD2；当A，C，E共线时，显然有（AC＋BC）2＝AB2＋4CD2，故结论成立．

（第16题）

（第17题）

17．如图①，分别以AC，BC为边向外作正△ACB′，△BCA′，连接BB′，AA′交于点P，则点P即为所求．

事实上，易证△BCB′≌△A′CA⇒∠B′BC＝∠AA′C．

故A′，B，P，C四点共圆．

从而∠BPA′＝∠BCA′＝60°．

因为∠APB′与∠BPA′为对顶角，所以，∠APB′＝∠BPA′＝60°．

在PB′上截取PD＝AP，连接AD，CP，得△APD为正三角形．易证△APC≌△ADB′⇒CP＝B′D⇒PA＋PB＋PC＝PD＋PB＋B′D＝BB′（定值）．

如图②，在△ABC内任取一点M（不同于点P），连接MA，MB，MC，

以点A为旋转中心，将△AMC逆时针旋转60°，使AC与AB′重合，得△AGB′．

则△AGB′≌△AMC⇒B′G＝CM．

连接GM，则△AGM为正三角形，有MA＝MG．

故MA＋MB＋MC＝MC＋MB＋B′G＝BM＋MG＋GB′＞BB′．

因此，点P到三个顶点A，B，C的距离之和最短（若以AB为边向外作正△ABC′，可得AA′＝BB′＝CC′）．

18．∵AB＜AO＋BO，CD＜CO＋DO，

∴AB＋CD＜AC＋BD　①，

又AB＋BD≤AC＋CD　②，

∴①＋②得2AB＜2AC，即AB＜AC．

19．将长方体沿DH，EA，HG展开，如图①，

将长方体沿EH，EF展开，如图②，

若蚂蚁从底面ABCD穿过，如图③，

将长方体沿GC展开，如图④，

（第19题）

故蚂蚁最少爬能找到糖．

20．如图，设a，b，c为△ABC的三边，ta，tb，tc为△ABC三个内角平分线，作∠ACE＝∠ADB，CE交AD延长线于点E．

由△ABD∽△AEC，得，即

同理，，

三式相乘得，即abc＞tatbtc．

（第20题）