黄金矩形可以分割成一个正方形和一个较小的黄金矩形,并且这种分割可以无限进行下去,分割后的黄金矩形,在大小不同的正方形内各画一个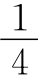 圆弧,就得到黄金螺线,黄金螺线被认为是自然界里最美的螺旋形状.
圆弧,就得到黄金螺线,黄金螺线被认为是自然界里最美的螺旋形状.
知能概述
通过寻找或构造相似三角形,用于计算或论证的方法,称为相似三角形法.线段长度的计算、角相等关系的证明、成比例线段的证明等问题常转化为相似三角形的判定.
熟悉以下“A形”“X形”“子母形”等相似三角形:
问题解决
例1 如图,△ABC中,∠ABC=60°,点P是△ABC内一点,使得∠APB=∠BPC=∠CPA,且PA=8,PC=6,则PB=________.
(全国初中数学联赛题)
解题思路 PA,PB,PC分别是△ABP,△BCP的边,从判定这两个三角形的关系入手.
一个学生不熟悉某个具体几何事实,他的损失并不大;如果未能掌握几何证明,他就丧失了获得严格论证训练的良机.
——波利亚
黄金矩形
什么样的矩形切去一个正方形后,剩下的矩形与原矩形相似?
如图,设矩形长、宽分别为x,y,则 =
=![]() ,解得
,解得![]() ≈0.618.我们把宽长之比为
≈0.618.我们把宽长之比为![]() 的矩形称为黄金矩形,这种矩形是让人感觉最美丽的矩形.
的矩形称为黄金矩形,这种矩形是让人感觉最美丽的矩形.
例2 如图,在直角梯形ABCD中,AB=7,AD=2,BC=3,如果边AB上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,那么这样的点P有( ).
A.1个 B.2个 C.3个 D.4个
(全国初中数学联赛题)
解题思路 通过代数化,将P点的个数的讨论转化为方程解的个数的讨论,因对应关系不确定,故需分类讨论.
例3 如图,四边形ABCD的各边相等,且∠ABC=60°,直线l过D点,但与四边形ABCD不相交(D点除外),l与BA,BC的延长线分别交于E,F,点M是CE与AF的交点.求证:CA2=CM·CE.
(亚太地区数学奥林匹克试题)
解题思路 只需证明△CAE∽△CMA,解题的关键是,通过其他三角形相似,为所证三角形相似提供条件.
例4 如图,H,Q分别是正方形ABCD的边AB,BC上的点,且BH=BQ,过B作HC的垂线,垂足为P,求证:DP⊥PQ.
(“祖冲之杯”竞赛题)
解题思路 即证∠QPC+∠DPC=90°,因∠BPQ+∠QPC=90°,只需证∠BPQ=∠DPC,证明△BPQ∽△CPD即可.
例5 如图,在△ABC中,AB=AC,AD⊥BC于D,E,G分别为AD,AC的中点,DF⊥BE于F,求证:FG=DG.
(湖北省武汉市竞赛题)
解题思路 若想证明∠GDF=∠GFD,则条件中的线段相等关系就难以用上.DG=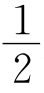 AC,以AC为桥梁,连接AF,CF,可证明∠AFC=90°.
AC,以AC为桥梁,连接AF,CF,可证明∠AFC=90°.
在证明两个三角形相似时,常常会出现证两次相似,而第一次相似常由两角相等证得,第二次相似常由第一次相似所得的比例线段进行恰当变化再加上夹角相等而证明.在具体证明过程中,常常要作等线段代换、等比代换或等积代换,以促使问题的转化.
相似三角形对应边成比例、对应角相等,由此可进一步证明线段倍分关系、和差关系、相等关系,判定两直线的位置关系.
相似三角形法进一步开阔了我们的解题视野,丰富了我们的解题思路.
例6 已知△ABC中,BC>AC,CH是AB边上的高,且满足![]() =
=![]() ,试探讨∠A与∠B的关系,并加以证明.
,试探讨∠A与∠B的关系,并加以证明.
(湖北省武汉市竞赛题)
分析与解 由题设条件易想到直角三角形中的基本图形、基本结论,可猜想出∠A与∠B的关系,解题的关键是综合运用勾股定理、比例线段的性质,推导判定两个三角形相似的条件.
(1)若垂足H在线段AB上,如图①,
由AH2+CH2=AC2,BH2+CH2=BC2,得
BH2-AH2=BC2-AC2,即(BH+AH)(BH-AH)=BC2-AC2,
又∠B是△ABC和△CBH的公共角,所以△ABC∽△CHB,∠ACB=∠CHB=90°,∠A+∠B=90°.
(2)若垂足H在BA的延长线上,如图②,作边CA关于CH的对称线段CA′,由(1)的结论知∠A′+∠B=90°,而∠A′=180°-∠A,代入上式得∠A-∠B=90°.
综合上述(1)、(2),我们有∠A+∠B=90°或∠A-∠B=90°.
例7 如图,已知△ABC的三边长为a,b,c,∠B=2∠C,求证:
(1)b<2c;
(2)b2=c(c+a).
(上海交通大学自主招生试题)
分析与解 怎样运用条件∠B=2∠C?作角平分线构造等角或向外构造等腰三角形.
进一步追问:
(1)若∠B=3∠C,则a,b,c又有怎样的关系?若∠B=n∠C呢?
(2)是否存在三边为连续自然数的三角形,使得最大角是最小角的两倍?最大角是最小角的三倍?
构造逆命题是提出问题的一个常用方法.例6是在直角三角形被斜边上的高分成的相似三角形得出的结论基础上提出的一个逆命题.你能提出新的问题吗?并加以证明.
由相似三角形得到的线段间的关系,不仅有比例式,还有等积式、平方式、线段乘积的和差、线段比的和差等,解复杂的线段间关系问题的基本方法是:
(1)对原式进行变形,促使问题转化;
(2)优先表示式子中的某些项,并由此展开推理.
如图,延长CB至D,使BD=AB.连接AD,则∠D=∠C,AD=AC=b.
(1)在△ABD中,b<2c.
(2)由△ADB∽△CDA得b2=c(c+a).
对于追问(2):存在这样的三角形,且三边长为4,5,6,最大角是最小角的两倍.另一种情形不存在.
相似性原理
自然界的许多现象和事物在形体、结构或方法、性质或量、质等方面存在某些共同点、相似点,这就是相似性原理.
类比推理是相似性原理的主要表现形式,即根据两个或两类对象在一系列属性上相同或相似,从而推断它们在其他属性上也相同或相似.
例8 探究证明:
(1)某班数学课题学习小组对矩形内两条相互垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:
如图①,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证![]()
结论应用:
(2)如图②,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上.若![]() ,则
,则![]() 的值为________;
的值为________;
联系拓展:
(3)如图③,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
(山东省烟台市中考题)
例7探寻了倍角三角形三边的关系,并在问题的广度和深度上作了进一步的发展.
请你思考:
在△ABC中,已知三边长分别为a,b,c,且∠C=2∠A=4∠B.求证: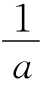 +
+ =
=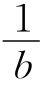 .
.
解题思路:
问题(3)是问题(1)的逆用,其关键是构造相应的矩形.
1.已知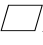 ABCD中,过点B的直线顺次与AC,AD及CD的延长线相交于点E,F,G,若BE=5,EF=2,则FG的长为________.
ABCD中,过点B的直线顺次与AC,AD及CD的延长线相交于点E,F,G,若BE=5,EF=2,则FG的长为________.
(上海市竞赛题)
(第1题)
(第2题)
(第3题)
2.如图,△ABC中,最大角∠A是最小角∠C的两倍,且AB=7,AC=8,则BC=________.
(全国初中数学联赛题)
3.如图,在 ABCD中,AM⊥BC,AN⊥CD,M,N为垂足.若AB=13,BM=5,MC=9,则MN的长为________.
ABCD中,AM⊥BC,AN⊥CD,M,N为垂足.若AB=13,BM=5,MC=9,则MN的长为________.
(江苏省竞赛题)
4.如图,O是正三角形ABC的边AC的中点,也是正三角形A1B1C1的边A1C1的中点,则AA1∶BB1=________.
(河北省竞赛题)
(第4题)
(第5题)
(第6题)
5.在四边形ABCD中,BC∥AD,CA平分∠BCD,O为对角线的交点,CD=AO,BC=OD,则∠ABC=________.(https://www.xing528.com)
(全国初中数学联赛题)
6.如图,在△ABC中,∠C=3∠A,AB=10,BC=8,则AC的长为________.
(上海市竞赛题)
7.如图,若PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=4,PD=3,则AD·DC=( ).
A.6 B.7
C.12 D.16
(第7题)
(全国初中数学联赛题)
8.如图,设AD,BE,CF为△ABC的三条高,若AB=6,BC=5,EF=3,则线段BE的长为( ).
(全国初中数学联赛题)
(第8题)
(第9题)
(第10题)
9.已知四边形ABCD为矩形,延长CB到E,使CE=CA,连接AE.F为AE的中点,连接BF,DF,DF交AB于点G.下列结论:
(1)BF⊥DF;
(2)S△BDG=S△ADF;
(3)EF2=FG·FD;
(4)![]()
其中正确的个数是( ).
A.1 B.2 C.3 D.4
10.如图,已知矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在线段
BC上,且![]() ,AF分别与DE,DB交于点M,N,则MN=( ).
,AF分别与DE,DB交于点M,N,则MN=( ).
(全国初中数学联赛题)
11.矩形ABCD中,AD=5,AB=10,E,F分别为矩形外的两点,BE=DF=4,AF=CE=3,则EF=( ).
(第11题)
(全国初中数学联赛题)
12.如图,设O为四边形ABCD的对角线AC与BD的交点,若∠BAD+∠ACB=180°,且BC=3,AD=4,AC=5,AB=6,则![]() =( ).
=( ).
(第12题)
(全国初中数学联赛题)
13.如图,D为等腰△ABC底边BC的中点,E,F分别为AC及其延长线上的点,又∠EDF=90°,ED=DF=1,AD=5,求线段BC的长.
(全国初中数学联赛题)
第13题)
(第14题)
(第15题)
14.如图,梯形ABCD中,AB∥CD,AB>CD,K,M分别是腰AD,CB上的点,已知∠DAM=∠CBK,求证:∠DMA=∠CKB.
(“祖冲之杯”竞赛题)
15.如图,在△ABC中,D,E分别是BC,AC的中点,AD,BE相交于P,若∠BPD=∠ACB.求证:以△ABC三中线为边构成的三角形与△ABC相似.
(湖北省武汉市竞赛题)
16.如图,在Rt△ABC中,∠C=90°,AM,AN分别为BC边上的中线和∠BAC的平分线.求证:MN·MC=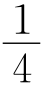 (AB-AC)2.
(AB-AC)2.
(第16题)
(四川省竞赛题)
17.在△ABC中,CA=CB,∠ACB=α.点P是平面内不与点A,C重合的任意一点,连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)观察猜想
如图①,当α=60°时,![]() 的值是________,直线BD与直线CP相交所成的较小角的度数是________;
的值是________,直线BD与直线CP相交所成的较小角的度数是________;
(2)类比探究
如图②,当α=90°时,请写出![]() 的值及直线BD与直线CP相交所成的较小角的度数,并就图②的情形说明理由;
的值及直线BD与直线CP相交所成的较小角的度数,并就图②的情形说明理由;
(3)解决问题
当α=90°时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时![]() 的值.
的值.
(第17题)
(河南省中考题)
18.如图,分别以锐角△ABC的边AB,BC,CA为斜边向外作等腰Rt△DAB,等腰Rt△EBC,等腰Rt△FAC.
求证:(1)AE=DF;
(2)AE⊥DF.
(全国初中数学联赛题)
(第18题)
(第19题)
(第20题)
19.如图,在△ABC中,M为BC的中点,D为AM延长线上的一点,且∠MBD=∠MAC,ME⊥AB于点E,MF⊥AC于点F.求证:![]()
(江苏省竞赛题)
20.如图,在锐角△ABC中,AD⊥BC于点D,H为AD上任一点,BH,CH的延长线分别交AC,AB于点E,F.求证:∠HDE=∠HDF.
(爱尔兰数学竞赛题)
例5 连接AF,CF,则△BFD∽△DFE,得![]()
∵CD=BD,DE=EA,∴![]() ,又∠FDC=∠FEA,
,又∠FDC=∠FEA,
∴△DFC∽△EFA,从而∠DFC=∠EFA.
又∵∠DFE=90°,∴∠AFC=90°,FG=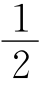 AC,而DG=
AC,而DG=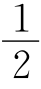 AC,故FG=DG.
AC,故FG=DG.
例8 (1)略
(2)![]()
(3)补全矩形ABEF,连接AC,BD,AC垂直平分BD,
则![]()
5.126° △ADO∽△CBO,OC=OD,∠ABC=∠ABD+∠DBC=54°+72°=126°.
6.3 如图,过C作∠C的三等分线CD,CE.
由△BDC∽△BCA,得BC2=BD·BA,BD=6.4,
又BE=BC=8,∴ED=1.6,AE=CE=2.
由△DCE∽△DAC,得DC2=DE·AD,DC=2.4,
又![]() ,得AC=3.
,得AC=3.
(第6题)
7.B 作∠APB的平分线交AD于点E,则![]() ,又△PDE∽△CDB,得
,又△PDE∽△CDB,得![]()
8.D 可证明△AFE∽△ACB.
9.C (2)错误;△BFG∽△DFB,![]()
10.C 延长DE,CB交于点G,则FN=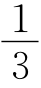 AN=
AN=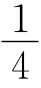 AF,
AF,![]() ,于是AM=
,于是AM=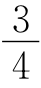 MF=
MF=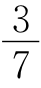 AF,MN=AF-AM-FN=
AF,MN=AF-AM-FN=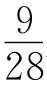 AF.
AF.
11.C 延长FA,EB交于点G,△BEC≌△DFA,△BGA∽△AFD,∠AGB=90°.
得∠PCK=∠PDM,∠BCK=∠ADM.
又∠DAM=∠CBK,∴△DAM∽△CBK,故∠DMA=∠CKB.
15.延长PD至F,使得DF=PD,连接BF,CF,PC,DE,则四边形BFCP为平行四边形,△PCF各边长为△ABC中线长的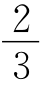 ,故△PCF与以△ABC三条中线为边的三角形相似,只需证明△PCF∽△ABC.
,故△PCF与以△ABC三条中线为边的三角形相似,只需证明△PCF∽△ABC.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




