八年级2020精英数学大视野第22讲：平行线分线段比例

0．618，这个比例数就是我们常说的“黄金分割数”．

达·芬奇系统研究了人类身体的各种比例，1509年，他为数学家帕西欧里的《神奇的比例》一书作插图，把人体与几何中简单的图形圆和正方形联系在一起，堪称艺术与科学的结晶，展示了达·芬奇对人体完美比例的浓厚兴趣，他是第一位借助数学来理解人体结构的自然科学家．

知能概述

三条平行线截两条直线，所得的线段对应成比例．

即如图，若l1∥l2∥l3，则，运用比例性质，可推得一系列的比例式．

在平行的条件下，上述图形、结论就演变成下列基本图形：

问题解决

例1　如图，在梯形ABCD中，AD∥BC，AD＝a，BC＝b，E，F分别是AD，BC的中点，且AF交BE于P，CE交DF于Q，则PQ 的长为________．

（上海市竞赛题）

解题思路　判断PQ与AD（或BC）的位置关系，建立含PQ的比例式．

没有数学公式的帮助，我很难传递出我心里的数学的旋律之美．

——伊藤清

梅涅劳斯定理

如图，一直线截△ABC的三边BC，CA，AB或其延长线于D，E，F，则

梅涅劳斯是古希腊数学家，他在三角学方面的成就，被称为希腊三角术的顶峰．

例2　如图，过△ABC的顶点B的两条直线分三角形BC边上的中线AD所成的比为AE∶EF∶FD＝4∶3∶1，则这两条直线分AC边所成的比AG∶GH∶HC为（　）．

A．4∶5∶3　B．3∶4∶2　C．2∶3∶1　D．1∶1∶1

（江苏省竞赛题）

解题思路　利用“广角镜”中问题的结论求解．

例3　如图，已知AB∥EF∥CD，AC＋BD＝240，BC＝100，EC＋ED＝192，求CF．

（山东省竞赛题）

解题思路　图形有多个基本图形，可写出不同的比例线段，解题的关键是恰当处理比例线段，从整体上求解．

例4　如图，在四边形ABCD中，AC与BD相交于点O，直线l平行于BD，且与AB，DC，BC，AD及AC的延长线分别相交于点M，N，R，S和P．求证：PM·PN＝PR·PS．

（山东省竞赛题）

解题思路　由于PM，PN，PR，PS在同一条直线上，所以不能直接应用平行线分线段成比例推得结论，需观察分解图形，利用中间比沟通不同比例式的关系．

例5　在△ABC中，已知D是BC边的中点，G是△ABC的重心，过G点的直线分别交AB，AC于点E，F．

（1）如图①，当EF∥BC时，求证：

（2）如图②，当EF和BC不平行，且点E，F分别在线段AB，AC上时，（1）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．

（3）如图③，当点E在AB的延长线上或点F在AC的延长线上时，（1）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．

（四川省乐山市中考题）

如图，过△ABC的顶点C任作一直线，与边AB及中线AD分别交于点F和E．求证：

为了运用平行线分线段成比例定理，需过一点作平行线，构造形如“A”形或“X”形基本图形．

随着过点作的平行线不同，就得到位置各异的基本图形，从而就有多种证题方法，读者不妨一试．

解题思路　对于（2），通过作平行线构造基本图形；对于（3），注意点E或F的特殊位置，关注BE与AE或CF与AF的大小比较．

例6　角平分线性质定理

例7　如图，四边形ABCD是梯形，点E是上底边AD上的一点，CE的延长线与BA的延长线交于点F，过点E作BA的平行线交CD的延长线于点M，BM与AD交于点N．求证：∠AFN＝∠DME．

（全国初中数学联赛题）

证明　延长BF和CM交于点P，延长ME与BC相交于点Q，

梯形“腰带”

如图，在梯形ABCD中，已知AD∥BC，AD＝a，BC＝b，E，F分别为AB，CD上的点，EF∥BC∥AD，我们形象地说线段EF为束在梯形上的“腰带”，随着这根“腰带”束在不同位置，EF的长与a，b有不同的数量关系．

例8　根据下列条件，求EF与a，b的关系：

（1）如图①，若EF为梯形中位线；

（2）如图②，若EF过梯形对角线的交点O；

（3）如图③，若梯形AEFD∽梯形EBCF；

（4）如图④，若S梯形AEFD＝S梯形EBCF．

平行线分线段成比例定理是证明比例线段的常用依据之一，比例线段丰富了我们研究几何问题的方法，主要体现在：

（1）利用比例线段求线段的长度；

（2）运用比例线段证明线段相等、线段和差倍分关系、两直线平行等问题．

平行线是我们学习几何时最早遇到的处于特殊位置的直线，平行线有如下重要作用：

（1）改变角的位置；

（2）传递线段；

（3）完成等积变形；

（4）产生比例线段．

从特殊到一般，运用相关定理可用a，b的代数式表示EF，我们会惊讶于代数中的重要概念、关系式统一在一个图形中．

1．如图，已知ABCD中，M，N为AB的三等分点，DM，DN分别交AC于P，Q两点，则AP∶PQ∶QC＝________．

（河北省竞赛题）

（第1题）

（第2题）

（第3题）

2．如图，在梯形ABCD中，AB∥CD，AB＝3CD，E是对角线AC的中点，BE延长后交AD于F，那么＝________．

（“祖冲之杯”竞赛题）

3．如图，已知△ABC，△DCE，△FEG，△HGI是4个全等的等腰三角形，底边BC，CE，EG，GI在同一直线上，且AB＝2，BC＝1．连接AI，交FG于点Q．则QI＝________．

（湖北省黄冈市中考题）

4．如图，工地上竖立着两根电线杆AB，CD，它们相距15m，分别自两杆上高出地面4m，6m的A，C处，向两侧地面上的E，D与B，F点处，用钢丝绳拉紧，以固定电线杆，那么钢丝绳AD与BC的交点P离地面的高度为________m．

（全国初中数学联赛题）

（第4题）

（第5题）

5．如图，在△ABC中，CD⊥AB于D，CE平分∠ACB，若AC＝15，BC＝20，CD＝12，则CE的长为________．

（“《数学周报》杯”全国初中数学竞赛题）

庞加莱（1854－1912），法国数学家，由于做出了杰出的工作，被认为是19世纪的后四分之一时期和20世纪初期的数学主宰，并且是对数学和它的应用最具有全面知识的、能雄观大局的通才．

6．如图，△ABC和△CDE都是等边三角形，且点A，C，E在同一直线上，AD与BE，BC分别交于点F，M，BE与CD交于点N，则下列结论正确的是________．①AM＝BN；②△ABF≌△DNF；③∠FMC＋∠FNC＝180°；④

（四川省宜宾市中考题）

7．如图，点E，F分别在菱形ABCD的边AB，AD上，且AE＝DF，BF交DE于点G，延长BF交CD的延长线于点H，若＝2，则的值为（　）．

（四川省绵阳市中考题）

（第6题）

（第7题）

（第8题）

8．如图，在△ABC中，D是AC的中点，E，F是BC的三等分点，AE，AF分别交BD于M，N两点，则BM∶MN∶ND等于（　）．

A．3∶2∶1　B．4∶2∶1　C．5∶2∶1　D．5∶3∶2

（湖北省武汉市竞赛题）(www.xing528.com)

9．如图，在正△ABC的边BC，CA上分别有点E，F，且满足BE＝CF＝a，EC＝FA＝b（a＞b），当BF平分AE时，则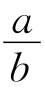的值为（　）．

（山东省竞赛题）

（第9题）

（第10题）

（第11题）

10．如图，在四边形ABCD中，∠BAC＝∠BDC＝90°，AB＝AC＝，CD＝1．对角线的交点为M，则DM＝（　）．

（全国初中数学联赛题）

11．如图，在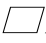ABCD中，E，F分别为边AB，AD上的点，EF与对角线AC

交于点P．若（a，b，m，n均为正数），则的值为（　）．

（天津市竞赛题）

12．如图，在△ABC中，，设r＝，其中P为CE与AD的交点，则r等于（　）．

（美国数学邀请赛试题）

（第12题）

（第13题）

（第15题）

13．如图，在等腰Rt△ABC中，F为AC边的中点，AD⊥BF于E，求证：BD＝2CD．

（云南省昆明市竞赛题）

14．探索发现：

已知：在梯形ABCD中，CD∥AB，AD，BC的延长线相交于点E．AC，

BD相交于点O，连接EO并延长交AB于点M，交CD于点N．

（第14题）

（1）如图①，如果AD＝BC，求证：直线EM是线段AB的垂直平分线．

（2）如图②，如果AD≠BC，那么线段AM与BM是否相等？请说明理由．

学以致用：

（3）仅用直尺（没有刻度），试作出图③中的矩形ABCD的一条对称轴（写出作图步骤，保留作图痕迹）．

（山东省威海市中考题）

15．如图，在梯形ABCD中，对角线AC与腰BC相等，M是底边AB的中点，L是腰DA延长线上的点，LM交BD于点N．求证：∠ACL＝∠BCN．

（四川省竞赛题）

16．如图，在梯形ABCD中，已知AB∥CD，O为对角线AC，BD的交点，P为腰AD，BC延长线的交点，PO交DC，AB分别为N，M．求证：AM＝BM，DN＝CN．

（乌克兰基辅数学奥林匹克试题）

（第16题）

（第17题）

17．如图，在四边形ABCD中，E，F分别是边AB，CD的中点．P为对角线AC延长线上的任意一点，PF交AD于点M，PE交BC于点N，EF交MN于点K．求证：K是线段MN的中点．

（江西省竞赛题）

18．如图，点E，F在正方形ABCD的边上，并且AE＝2ED，DF＝2FC，AF交BE于点G，求的值．

（世界数学团体锦标赛试题）

（第18题）

19．AD是△ABC的中线，将BC边所在直线绕点D顺时针旋转α角，交边AB于点M，交射线AC于点N，设AM＝xAB，AN＝yAC（x，y≠0）．

（1）如图①，当△ABC为等边三角形且α＝30°时，证明：△AMN∽△DMA；

（2）如图②，证明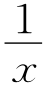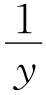：＋＝2；

（3）如图③，当G是AD上任意一点时（点G不与A重合），过点G的直线交边AB于M′，交射线AC于点N′，设AG＝nAD，AM′＝x′AB，AN′＝y′AC（x′，y′≠0），猜想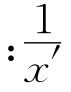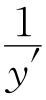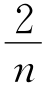＋＝是否成立？并说明理由．

（湖北省黄石市中考题）

（第19题）

20．过梯形的一个顶点作两条直线l1，l2，其中直线l1是梯形的对角线，并且将梯形两底边中点的连线分成的比为3∶1，直线l2等分梯形的面积，求直线l2将梯形两底边中点的连线分成的比值．

（俄罗斯数学竞赛题）

1．5∶3∶12　2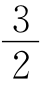．　延长BF与CD延长线交于点P．

3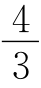．　由AC∥FG，得，QI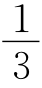＝AI，过点A作AM⊥BI于点M．

4．

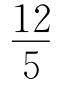
13．下面思路仅供参考：作CG∥AB交AD延长线于点G．

14．（1）略　（2）相等，证明略．

（3）作法：如图．

①连接AC，BD，两线交于点O1；

②在矩形ABCD外任取一点E，连接EA，EB，分别交DC于点G，H；

③连接BG，AH，两线交于点O2；

④作直线EO2，交AB于点M；

⑤作直线MO1．

则直线MO1就是矩形ABCD的一条对称轴．

（第14题）

15．如图，延长CN交AB于点F，延长LN，DC交于点G．

∵AM∥DG，BM∥DG．∴，得

而AM＝MB，则AE＝BF．

∵AC＝BC，∠CAB＝∠CBA，∴△ACE≌△BCF．

故∠ACL＝∠BCN．

16．由，得

两式相乘得，故AM＝MB，同理可证：DN＝NC．

（第15题）

17．在PF上取点G，使GF＝FM，CG∥DM，又取CA的中点L，连接GC，GN，LE，LF，则LE，LF分别为△ABC，△ACD的中位线，有LF∥AD，LE∥CB，得∠GCN＝∠FLE，故△CNG∽△LEF，NG∥EF，于是FK为△MNG中位线，故K是MN的中点．

（第17题）

18．分别延长BE和CD，交于点P，设正方形ABCD的边长为3，则PD＝，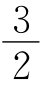

19．（1）略

（2）如图①，作CF∥AB交MN于点F，则△CFN∽△AMN，

∴

∵CF∥AB，∴∠B＝∠DCF，

又∠MDB＝∠CDF，BD＝DC，

∴△CFD≌△BMD，

∴BM＝CF．

（第19题）

（第20题）