精英数学大视野·八年级2020：探索英国海岸线长度

英国的海岸线有多长？1967年法国数学家曼德布罗特在《科学》杂志上就此发表了一篇论文，并给出惊人的结论：没有准确的答数．

曼德布罗特认为，云彩不是球体，山岭不是锥体，海岸线不是圆周，闪电更不是沿着直线传播的，数学家不能回答这些大自然提出的问题．

知能概述

线段的中点是几何图形中一个特殊的点，它关联着中线、中心对称图形、中位线等丰富的知识，在线段的计算、线段倍分关系的证明、角的相等关系的证明、两直线位置关系的判定等方面有广泛的应用．

熟悉以下基本图形、基本结论：

问题解决

例1　如图，在△ABC中，∠B＝2∠C，AD⊥BC于点D，M为BC的中点，AB＝10cm，则MD的长为________．

（“希望杯”邀请赛试题）

解题思路　取AB的中点或AC的中点．

数学家像画家和诗人一样，是模式制造家．

——哈代

凯纳斯多边形

如图，任意画一个平面多边形P0，作出其各边中点，按顺序连接成一个新的多边形P1，对P1重复以上操作得到P2，继续下去，则得到一个多边形序列｛P0，P1，P2，…，Pm，…｝．我们称Pm为Pm－1的凯纳斯多边形，其中m为正整数．

数学家凯纳斯对这种多边形作过研究，发现以下结论：｛P1，P3，…，P2n＋1，…｝从形状上逼近一个确定的n边形P，而｛P2，P4，…，P2n，…｝则从形状上逼近另一个确定的n边形Q，且P与Q内接于同一个椭圆．

例2　如图，已知M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB＝10，BC＝15，MN＝3，则△ABC的周长为（　）．

A．38　B．39　C．40　D．41

（四川省竞赛题）

解题思路　添加辅助线可得到异于M的中点．

例3　如图，已知AD是△ABC的角平分线，AB＜AC，在AC上截取CE＝AB，M，N分别为BC，AE的中点．求证：MN∥AD．

（山西省太原市竞赛题）

解题思路　角平分线、中点、平行线，能引起丰富的联想，而构造中位线、中心对称图形能架构连接各种分散条件的桥梁，使得思维充分发散．

对于图①，连接BE，取BE中点F，连接NF，MF．

对于图②，在AC上截取AF＝AB，连接BF，交AD于H，连接MH．

对于图③，连接AM并延长到F，使MF＝AM，连接EF，FC．

例4　如图，在△ABC内取一点P，使∠PBA＝∠PCA，作PD⊥AB于点D，PE⊥AC于点E，求证：DE的垂直平分线必经过BC的中点M．

解题思路　设M为BC的中点，将问题转化为证明MD＝ME，利用中点构造全等三角形．

需要什么，构造什么．构造基本图形、构造线段的和差（倍分）关系、构造角的关系等，是作辅助线的有效思考方法．

当问题的条件涉及三角形一边的中点和直角三角形时，常取斜边中点，从而把直角三角形斜边中线定理与三角形中位线定理联系起来．

例5　如图①，P是线段AB上的一点，在AB的同侧作△APC和△BPD，使∠APC＝∠BPD，PC＝PA，PD＝PB，连接CD，点E，F，G，H分别是AC，AB，BD，CD的中点，顺次连接E，F，G，H．

（1）猜想四边形EFGH的形状，直接回答，不必说明理由；

（2）当点P在线段AB的上方时，如图②，在△APB的外部作△APC和△BPD，其他条件不变，（1）中结论还成立吗？说明理由；

（3）如果（2）中，∠APC＝∠BPD＝90°，其他条件不变，先补全图③，再判断四边形EFGH的形状，并说明理由．

（辽宁省营口市中考题）

解题思路　结论随着条件的改变也许发生变化，但解决问题的方法是一致的，即通过连线，为三角形中位线定理的应用创造条件．

例6　如图，在任意五边形ABCDE中，M，N，P，Q分别为AB，CD，BC，DE的中点，K，L分别为MN，PQ的中点．求证：KL∥AE且KL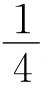＝AE．

（天津市竞赛题）

分析与解　恰当连接五边形对角线，为构造三角形中位线创造条件．

连接BE，取其中点R，连接MR，则连接RN，则P，N，Q，R分别为四边形BCDE各边的中点．

∴四边形PNQR为平行四边形，RN，PQ互相平分．

∵L为PQ的中点，∴L为RN的中点．

在△MNR中，，故

如图，顺次连接四边形ABCD各边中点，得到四边形A′B′C′D′，称为中点四边形，中点四边形A′B′C′D′有下列重要性质：

（1）为平行四边形；

（2）S▱A′B′C′D′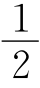＝S四边形ABCD；

（3）A′B′C′D′随原四边形对角线的改变而变为特殊平行四边形；

（4）当原四边形为凹四边形时，其他条件不变，上述结论仍然成立．

例7　如图，已知△ABC中，∠ACB＝90°，AB边上的高CH与△ABC的两条内角平分线AM，BN分别交于P，Q两点，PM，QN的中点分别为E，F．求证：EF∥AB．

（全国初中数学联赛题）

分析与解　从图形的形成过程，逐步探索相应结论．将原问题分解为多个小问题．

（1）如图①和②，△CPM，△CNQ皆为等腰三角形，连接CE，CF，则CE⊥PM，CF⊥NQ．

（2）如图③，分别延长CE，CF交AB于S，R，则

中垂三角形

在几何学中，我们研究过两种特殊三角形：等腰三角形、直角三角形，而“中垂三角形”也具有丰富的图形性质，等待我们的探索．

例8　我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图①、图②、图③中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均为“中垂三角形”．设BC＝a，AC＝b，AB＝c．

特例探索：

（1）如图①，当∠ABE＝45°，c＝时，a＝________，b＝________；如图②，当∠ABE＝30°，c＝4时，a＝________，b＝________；

归纳证明：

（2）请你观察（1）中的计算结果，猜想a2，b2，c2三者之间的关系，用等式表示出来，并利用图③证明你发现的关系式；

例7表明：一些综合题常是几个简单、熟悉的典型题组合、嫁接而成，模式识别、分解基本图形、化大为小，是解综合题的重要策略．

对于中垂三角形还能推得以下结论：

（1）S△ABC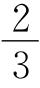＝AF·BE；

（2）设CG为其第三条边上的中线，则

（3）以AF，BE，CG的长为边必构成一直角三角形．

你能证明吗？

拓展应用：

（3）如图④，在ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG，AD＝，AB＝3．求AF的长．

（江西省中考题）

解题思路　从特殊到一般，借助勾股定理、中位线性质探索a2，b2，c2之间的关系．对于（3），逆向构造“中垂三角形”，为其性质的运用创造条件．

1．如图，四边形ABCD的对角线AC，BD相交于点F，M，N分别为AB，CD中点，MN分别交BD，AC于P，Q，且∠FPQ＝∠FQP，若BD＝10，则AC＝________．

（重庆市竞赛题）

（第1题）

（第2题）

（第3题）

2．如图，在菱形ABCD中，∠A＝100°，M，N分别是边AB，BC的中点，MP⊥CD于点P，则∠NPC 的度数为________．

（山东省竞赛题）

3．如图，在矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB 的最小值是________．

（山东省泰安市中考题）

4．如图，在Rt△ABC中，∠BAC＝90°，M，N是BC边上的点，BM＝MN＝NC，如果AM＝4，AN＝3，则MN＝________．

（第4题）

（第5题）

5．如图，在△ABC中，∠BAC＝120°，以AB，AC为边向外作等边△ABD和等边△ACE．M为AD中点，N为AE中点，P为BC中点，则∠MPN的度数为________．

（北京市竞赛题）

1904年，法国数学家庞加莱提出这一猜想．庞加莱猜想的证明有助于人类解决宇宙形状之谜．

6．（1）如图①，将四边形纸片ABCD沿两组对边中点连线剪切为四部分，将这四部分密铺可得到如图②所示的平行四边形．若要使密铺后的平行四边形为矩形，则四边形ABCD 需要满足的条件是________；

（山东省威海市中考题）

（第6题）

（2）如图③，在菱形ABCD中，边长为10，∠A＝60°．顺次连接菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连接四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连接四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去……则四边形A2B2C2D2的周长是________；四边形A2013B2013C2013D2013的周长是________．

（浙江省衢州市中考题）

7．如图，在四边形ABCD中，一组对边AB＝CD，另一组对边AD≠BC，分别取AD，BC的中点M，N，连接MN，则AB与MN的关系是（　）．

A．AB＝MN　B．AB＞MN

C．AB＜MN　D．以上三种情况均可能出现

（河北省竞赛题）

（第7题）

（第8题）

（第9题）

8．如图，边长为1的正方形EFGH在边长为3的正方形ABCD所在平面上移动，始终保持EF∥AB，线段CF，DH的中点分别为M，N，则线段MN的长为（　）．

（北京市竞赛题）

9．如图，已知凸五边形ABCDE，∠ABC＝∠AED＝90°，∠DAC＝30°，∠BAE＝70°，F是边CD的中点，且FB＝FE，则∠BAC等于（　）．

A．10°　B．20°　C．30°　D．15°

（四川省竞赛题）

10．如图，已知△ABC的周长为24，M是AB的中点，MC＝MA＝5，则△ABC的面积是（　）．

A．30　B．24　C．16　D．12

（全国初中数学联赛题）

（第10题）

（第11题）

（第12题）

11．已知四边形ABCD为任意凸四边形，E，F，G，H分别是边AB，BC，CD，DA的中点，用S，p分别表示四边形ABCD的面积和周长．S1，p1分别表示四边形EFGH的面积和周长，设，则下面关于k，k1的说法正确的是（　）．

A．k，k1均为常值　B．k为常值，k1不为常值(www.xing528.com)

C．k不为常值，k1为常值　D．k，k1均不为常值

（全国初中数学联赛题）

12．如图，在四边形ABCD中，AC＝a，BD＝b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……如此进行下去，得到四边形AnBnCnDn．下列结论：①四边形A4B4C4D4是菱形；②四边形A3B3C3D3是矩形；③四边形A7B7C7D7的周长为；④四边形AnBnCnDn的面积为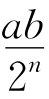．其中正确的是（　）．

A．①②③　B．②③④　C．①③④　D．①②③④

（湖北省鄂州市中考题）

13．如图，在△ABC中，AC＝7，BC＝4，D为AB的中点，E为边AC上一点，且∠AED＝90°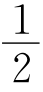＋∠C，求CE的长．

（“华罗庚金杯”少年数学邀请赛试题）

（第13题）

（第14题）

14．如图，在梯形ABCD中，AD∥BC，AC⊥BD于O，试判断AB＋CD与AD＋BC的大小，并证明你的结论．

（山东省竞赛题）

15．如图，在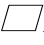ABCD的内部取一点E，使得AE＝DE，∠ABE＝90°，设M为BC的中点，求∠DME的大小．

（俄罗斯数学竞赛题）

（第15题）

（第16题）

16．如图，在锐角△ABC中，AD⊥BC于D点，BE⊥AC于点E，且AD与BE交于点H，M，N分别是边AB，CH的中点．求证：MN⊥DE．

（“宗沪杯”竞赛题）

17．某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程：

（1）操作发现：

在等腰△ABC中，AB＝AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图①所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是________（填序号即可）．

（第17题）

①AF＝AG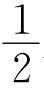＝AB；②MD＝ME；③整个图形是轴对称图形；

④∠DAB＝∠DMB．

（2）数学思考：

在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图②所示，M是BC的中点，连接MD和ME，则MD与ME具有怎样的数量和位置关系？请给出证明过程．

（3）类比探究：

在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图③所示，M是BC的中点，连接MD和ME，试判断△MED的形状．答_______：_．

（江西省中考题）

18．如图，已知AB＝AC，∠BAC＝∠CDE＝90°，DC＝DE，F为BE的中点．证明：FA＝FD，且FA⊥FD．

（第18题）

（四川省竞赛题）

19．在六边形ABCDEF中，AB∥DE，BC∥EF，CD∥FA，AB＋DE＝BC＋EF，A1D1＝B1E1，A1，B1，D1，E1分别是边AB，BC，DE，EF的中点．求证：∠CDE＝∠AFE．

（北京市竞赛题）

（第19题）

（第20题）

20．已知点M在凸四边形ABCD内，且AM＝BM，CM＝DM，∠AMB＝∠CMD＝60°，设BC，AM，DM的中点分别为K，L，N，求∠LKN的大小．

（白俄罗斯数学竞赛题）

例1　5　可以证明MD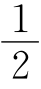＝AB．

例2　D　延长BN交AC于D，则MN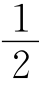＝CD．

例3　用图①给出证明：

如图，∵，且CE＝AB，∴FN＝FM，∠3＝∠4＝∠5．

又∠1＋∠2＝∠3＋∠5，而∠1＝∠2．

则∠2＝∠5，故MN∥AD．

例4　如图，设L，N分别是PB，PC的中点，连接MD，ME，ML，MN，DL，EN，则

由∠PDB＝∠PEC＝90°，得DL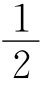＝PB，EN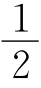＝PC，

∴DL＝MN，ML＝EN，且四边形PLMN为平行四边形，

于是∠PLM＝∠PNM．

又∠DLP＝2∠PBA＝2∠PCA＝∠ENP，

∴∠DLM＝∠DLP＋∠PLM＝∠ENP＋∠PNM＝∠ENM，

∴△DML≌△MEN，故DM＝EM．

例5　（1）四边形EFGH是菱形．

（2）成立，连接AD，BC，由△APD≌△CPB，得AD＝CB，

又EF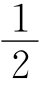＝BC，FG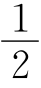＝AD，GH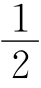＝BC，EH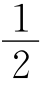＝AD，则EF＝FG＝GH＝EH，故四边形EFGH是菱形．

（3）四边形EFGH是正方形，在（2）的基础上，证明∠EHG＝90°即可．

（例3）

（例4）

例8　（1）

（2）a2＋b2＝5c2．

∵

（例8）

化简得a2＋b2＝5c2．

（3）如图，取AB的中点H，连接FH，AC．设AF，BE交于点P．

∵点E，G分别是AD，CD的中点，点F是BC的中点，∴EG∥AC∥FH．又∵BE⊥EG，∴FH⊥BE．∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴AE＝BF，AE∥BF，∴AP＝FP，∴△ABF是中垂三角形，∴AB2＋AF2＝5BF2，即32＋AF2＝，∴AF＝4．

1．10　2．50°　取MP的中点E，连接NE，则NE∥BM∥CP，NE⊥MP，NM＝NP．

3．如图，连接DE，分别取DE，DC中点M，N，连接MN，BN，△ADE，△BCE，△DEC都为等腰直角三角形，点P的运动路径为线段MN，BN⊥MN，即BN为BP的最小值，

4．作MD⊥AC于点D，NE⊥AC于点E，设AD＝DE＝EC＝x，NE＝y，则MD＝2y．

5．60°　连接DE，MN，BM，CN，可以证明△MNP为等边三角形．

6．（1）AC＝BD

（第3题）

（2）20，当n为偶数时，中点四边形为菱形；当n为奇数时，中点四边形为矩形，其周长为

7．B

8．B　连接CG，取CG的中点T，连接MT，NT，则MT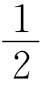＝，NT＝2，∠MTN＝90°．

9．B　取AC中点P，AD中点Q，连接BP，PF，QF，EQ，则△BPF≌△EQF，可证明∠BAC＝∠EAD．

10．B　MC＝MA＝MB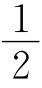＝AB，∠ACB＝90°．

11．B

13．作BF∥DE交AC于点F，作∠ACB的平分线交AB于点G，交BF于点H，则∠AED＝∠AFB＝∠CHF＋∠C，由∠AED＝90°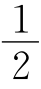＋∠C，得∠CHF＝90°＝∠CHB，CF＝CB＝4，从而CE＝5．5．

14．取AB中点M，CD中点N，连接MN，OM，ON，可推得AB＋CD＞AD＋BC．

15．如图，取AD中点N，连接BN，MN，NE，则四边形ABMN，四边形BMDN均为平行四边形，

∵BE⊥AB，AE＝DE，

∴E为△BMN三边高的交点，

∴ME⊥BN，而BN∥DM，

∴∠DME＝90°．

16．连接MD，ME，连接ND，NE，可证明MD＝ME，ND＝NE，从而MN是线段DE的垂直平分线，故MN⊥DE．

17．（1）①②③④

（2）分别取AB，AC的中点F，G，连接DF，MF，MG，EG，证明△DFM≌△MGE，可推得MD＝ME且MD⊥ME．

（3）等腰直角三角形

18．连接BC，CE，再参见第16题．

（第15题）

（第19题）

在△B1ME1与△A1ND1中，B1M＝A1N，E1M＝D1N．

又因为A1D1＝B1E1，所以，△B1ME1≌△A1ND1．

因此∠B1ME1＝∠A1ND1．

故∠CDE＝∠AFE．

20．如图，记线段BM，CM的中点分别为E，F，连接EL，LN，NF，FK，KE．

∵∠AMB＝∠CMD＝60°，

∴∠BMC＝360°－∠AMB－∠CMD－∠LMN

＝360°－60°－60°－∠LMN

＝240°－∠LMN．

由KF为△CBM的中位线，得KF∥BM

∴∠KFM＝180°－∠BMC＝180°－（240°－∠LMN）＝∠LMN－60°．

由CM＝DM且∠CMD＝60°，知△CMD为等边三角形．

又FN为△CMD的中位线，则△FMN也为等边三角形，即

FM＝NM＝FN，∠MFN＝60°．故∠KFN＝∠KFM＋∠MFN＝∠LMN－60°＋60°＝∠LMN．

类似的，∠KEL＝∠LMN，EM＝ML＝EL．

从而，△KEL≌△NFK≌△NML，则KL＝KN＝LN．

故△KLN为等边三角形，∠LKN＝60°．

（第20题）