第20讲：梯形的解析方法及应用

如图，将一个正方形九等分，然后挖去中间的一个；再将剩下的八个小正方形各自九等分后分别挖去中间的一个小正方形，重复上面的步骤，就可得到谢尔宾斯基地毯，它的面积趋于0，而各正方形周长之和趋于无穷大．

知能概述

通过添加辅助线，把梯形转化成平行四边形或三角形，这是解梯形问题时的主要思路，具体做法是：过一顶点作一腰的平行线、过顶点作一对角线的平行线、延长两腰、过底的顶点作另一底的垂线等．

熟悉以下基本图形、基本结论：

问题解决

例1　（1）如图①，四边形ABCD中，AB∥CD，∠D＝2∠B，若AD＝a，AB＝b，则CD的长是________；

（“希望杯”邀请赛试题）

（2）如图②，梯形两底角之和为90°，上底长为5，下底长为11，则连接两底中点的线段MN长是________．

（安徽省竞赛题）

解题思路　平移腰，构造等腰三角形或直角三角形．

数学一般通过直接激发创造精神和活跃思维的方式来提供其最佳服务．

——赫巴特

几何分割

几何分割并不需要太多的数学知识，没有现成的章法可循，依据的是想象力和直觉．

如图，有些几何图形通过分割可以复制出一些小的相似图形．

例2　已知一个梯形的4条边的长分别为1，2，3，4，则此梯形的面积等于（　）．

（全国初中数学联赛题）

解题思路　给出4条线段，要构成梯形需满足一定条件，解题的关键是确定可能的上、下底．

例3　如图，在等腰梯形ABCD中，AB∥DC，AB＝998，DC＝1001，AD＝1999，点P在线段AD上，问：满足条件∠BPC＝90°的点P有多少个？

（全国初中数学联赛题）

解题思路　本例是以下面问题为基础：在梯形ABCD中，AD∥BC，AD＋BC＝DC．

（1）如图①，若E为AB中点，则∠DEC＝90°且CE，DE分别平分∠BCD，∠ADC；

（2）如图②，在CD上取一点M，使MD＝AD，连接BM，则∠AMB＝90°；

（3）如图③，将①②组合，则四边形GEHM为矩形．

例4　如图①，四边形ABCD是等腰梯形，AB∥DC，由四个这样的等腰梯形可以拼出图②所示的平行四边形．

（1）求四边形ABCD四个内角的度数；

（2）试探究四边形ABCD四条边之间存在的等量关系，并说明理由；

（3）现有图①中的等腰梯形若干个，利用它们你能拼出一个菱形吗？若能，请你画出大致的示意图．

（山东省中考题）

相同的条件，不同的结论；相同的“原料”，不同的“菜肴”，一个基础性问题，通过变式、重组以及强化、弱化条件等方式，可生成问题系列．

故在学习中储备、掌握典型问题，有利于提高解题的起点．

例4是一类图形信息题，即通过图形展示信息，它打破了用语言描述数量、位置关系的传统，而将其隐含在问题的图中，解题时应认真观察图形，根据图形的结构特点、性质，从中提取信息，为解题服务．

解题思路　对于（1）、（2），在观察的基础上易得出结论，探寻上、下底和腰及上下底之间的关系，从作出梯形的常用辅助线入手；对于（3），在（2）的基础上，展开想象的翅膀，就可设计出若干种图形．

例5　连接凸四边形一组对边中点的线段等于另一组对边和的一半，问：这个凸四边形是什么四边形？试证明你的结论．

（俄罗斯莫斯科市数学奥林匹克试题）

解题思路　由中点想到中位线，连接对角线并取其中点，为中位线定理的应用创造条件．

例6　如图，在等腰梯形ABCD中，CD∥AB，对角线AC，BD相交于O，∠ACD＝60°，点S，P，Q分别为OD，OA，BC的中点．

（1）求证：△SPQ是等边三角形；

（2）若AB＝5，CD＝3，求△SPQ的面积；

（3）若△SPQ的面积与△AOD的面积的比是7∶8，求梯形上、下两底的比CD∶AB．

（“希望杯”邀请赛试题）

解　连接SC，PB．

等腰梯形与等腰三角形有着内在联系，体现在：

（1）它们有相似性质；

（2）连接等腰梯形对角线，就得到等腰三角形，故解等腰梯形有关问题时，需综合运用等腰三角形的相关知识．

故CD∶AB＝1∶2．

例7　如图，分别以△ABC的边AC和BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点．求证：点P到边AB的距离是AB的一半．

（山东省竞赛题）

证明　如图，分别过E，F，C，P作AB的垂线，垂足依次为R，S，T，Q，则PQ就是点P到AB的距离，且有ER∥PQ∥CT∥FS，故四边形ERSF为直角梯形，PQ＝（ER＋FS）．

易证Rt△AER≌Rt△CAT，Rt△BFS≌Rt△CBT，

∴ER＝AT，FS＝BT，

又AT＋BT＝AB＝ER＋FS，

故PQ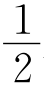＝AB．

寻找关联

一些“风马牛不相及”的问题之间常有着千丝万缕的联系．通过探究，寻找关联，可体悟数学问题的结构之美．

例8　（1）如图①，在△ABC中，已知AB＝AC，D为BC边上的一点，求证：AB2－AD2＝BD·CD；

（2）如图②，在等腰梯形ABCD中，已知AD∥BC，AB＝CD，求证：BD2－AB2＝AD·BC．

“问愈透，创更新”是李政道当年在芝加哥理工大学与导师费米教学互动时的感悟．批判性阅读、批判性聆听、独立思考，是催生创新之花盛开、创新之树常绿的关键．

解题思路　通过构造等腰梯形，可由问题（1）推证问题（2），反之亦然．

1．（1）等腰梯形被对角线分为两个等腰三角形，则等腰梯形的各角度数为________；

（俄罗斯莫斯科市数学奥林匹克试题）

（2）若等腰梯形的大底等于对角线长，小底等于高长，则小底与大底的比是________．

（江苏省竞赛题）

2．已知矩形纸片ABCD中，AB＝1，BC＝2．将该纸片折叠成一个平面图形，折痕EF不经过A点（E，F是该矩形边界上的点），折叠后点A落在点A′处，给出以下判断：

（第2题）

①当四边形A′CDF为正方形时，EF＝；

②当EF＝时，四边形A′CDF为正方形；

③当EF＝时，四边形BA′CD为等腰梯形；

④当四边形BA′CD为等腰梯形时，EF＝

其中正确的是________（把所有正确结论的序号都填在横线上）．

（安徽省中考题）

3．如图，已知四边形ABCD为等腰梯形，AB∥CD，AB＝6，CD＝16，△ACE为直角三角形，∠AEC＝90°，CE＝BC＝AD，则AE 的长为________．

（上海市竞赛题）

（第3题）

（第4题）

（第5题）

4．如图，在梯形ABCD中，AD∥BC，AB＝8，AD＝3，CD＝6，并且∠B＋∠C＝90°，则该梯形的面积S＝________．

（河北省竞赛题）

5．如图，在梯形ABCD中，AD∥BC（BC＞AD），∠D＝90°，BC＝CD＝12，∠ABE＝45°．AE＝10，则CE的长为________．

（全国初中数学联赛题）

6．庄子说：“一尺之棰（短棍），日取其半，万世不竭（尽，完）．”这句话（文字语言）表达了古人将事物无限分割的思想，可用图形语言表示为图①．按此图的分割方法，可得到一个等式（符号语言）：1＝＋＋＋…＋＋…．

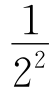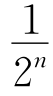（第6题）

图②也是一种无限分割：用3个相同的等边三角形△DOA，△AOB，△BOC拼成一个等腰梯形ABCD，将它分成4个全等的等腰梯形DD1A1A，AA1B1B，BB1C1C和A1B1C1D1，再将下方的等腰梯形A1B1C1D1分成4个全等的等腰梯形D1A1A2D2，A1B1B2A2，B1C1C2B2，A2B2C2D2……如此继续无限分割下去．设原等腰梯形ABCD的面积为1，利用阴影部分所有等腰梯形ABB1A1，A1B1B2A2，A2B2B3A3，…的面积和，可以得到一个等式，则这个等式为________．

（《时代学习报》数学文化节试题）(www.xing528.com)

7．用4条线段a＝14，b＝13，c＝9，d＝7作为4条边构成一个梯形，则在所构成的梯形中，中位线长的最大值为（　）．

A．13．5　B．11．5　C．11　D．10．5

（湖北省竞赛题）

8．如图，在梯形ABCD中，AD∥BC，AD＝2，AC＝4，BC＝6，BD＝8，那么梯形ABCD的面积为（　）．

（湖北省武汉市竞赛题）

（第8题）

（第9题）

（第10题）

9．在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2，4，3，则原直角三角形纸片的斜边长是（　）．

（安徽省中考题）

10．如图，在梯形ABCD中，AD∥BC，∠B＝30°，∠C＝60°，E，M，F，N分别为AB，BC，CD，DA的中点，已知BC＝7，MN＝3，则EF的长为（　）．

（全国初中数学联赛题）

11．如图，已知四边形ABCD各边长均为正整数，周长为P，∠B＝∠C＝90°，AB＝2，CD＝AD．若P＜2015，则正整数P有（　）个不同的可能值．

A．30　B．31　C．61

D．62　E．63

（第11题）

（美国数学竞赛题）

12．如图，在平面直角坐标系中，等腰梯形ABCD的顶点坐标分别为A （1，1），B（2，－1），C（－2，－1），D（－1，1）．y轴上一点P（0，2）绕点A旋转180°得点P1，点P1绕点B旋转180°得点P2，点P2绕点C旋转180°得点P3，点P3绕点D旋转180°得点P4，……，重复操作依次得到点P1，P2，…，则点P2010的坐标是（　）．

A．（2010，2）　B．（2010，－2）

C．（2012，－2）　D．（0，2）

（“《数学周报》杯”全国初中数学竞赛题）

（第12题）

（第13题）

（第14题）

13．如图，在梯形ABCD中，AD∥BC，AC⊥DB，AC＝5，∠DBC＝30°．

（1）求对角线BD的长度；

（2）求梯形ABCD的面积．

（四川省竞赛题）

14．如图，在梯形ABCD中，AB∥DC，M是腰BC的中点，MN⊥AD．求证：S梯形ABCD＝MN·AD．

（山西省竞赛题）

15．如图，在四边形ABCD中，AD∥BC，AB＝AC，DF⊥BC于点F，DF与AC交于点E，若BE＝2DF，且BE平分∠ABC，求∠BAD的度数．

（青少年数学国际城市邀请赛试题）

（第15题）

（第16题）

16．如图，在锐角△ABC中，作高BD和CE，过顶点B，C分别作ED的垂线BF和CG．求证：EF＝DG．

（俄罗斯数学竞赛题）

17．如图，在梯形ABCD中，AD∥BC，分别以两腰AB，CD为边向两边作正方形ABGE和正方形DCHF，设线段AD的垂直平分线l交线段EF于点M．求证：点M为EF的中点．

（全国初中数学联赛题）

（第17题）

18．“标准等腰梯形”是指只有一对平行边的等腰梯形（例如，平行四边形、长方形均不为标准等腰梯形）．将一个长方形分成不一定全等的n个标准等腰梯形的一种分割是“严格的”．当且仅当对于任意满足2≤i≤n的i，均不存在（不经过平移、旋转与拼接）能构成一个大标准等腰梯形的i个小等腰梯形（换句话说，该分割是严格的，如果它不是另一种标准等腰梯形更少的分割的再细分）．证明：对一切不小于9的正整数n，均存在一种将一个2017×2018的长方形分成n个标准等腰梯形的严格分割．

（塞尔维亚数学竞赛题）

例1　（1）b－a　过C作CE∥AD交AB于E．

（2）3　作CF∥AD交AB于F，作Rt△FCB斜边中线CE，则CE＝MN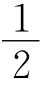＝（AB－CD）．

例2　D　以1，2，3，4为边长作梯形只有以下六种可能：①1，2为底；②1，3为底；③1，4为底；④2，3为底；⑤2，4为底；⑥3，4为底，只有③才能构成梯形．如图，设在梯形ABCD中，AB＝3，BC＝4，CD＝2，DA＝1，作AH⊥BC于H，AE∥DC交BC于E，则BA＝BE，由，得AH＝，故S梯形ABCD＝

（例2）

例3　当P为AD中点时，可以证明∠BPC＝90°；在AD上截取AP＝AB，可以证明∠BPC＝90°，故满足条件∠BPC＝90°的点P有2个．

例4　（1）上底角为120°，下底角为60°．

（2）梯形的上底等于下底的一半，且等于腰长．

（3）能拼出菱形，如图，供参考．

（例4）

例5　这个凸四边形是平行四边形或梯形．证明如下：如图，在凸四边形ABCD中，M，N分别是对边AB，CD的中点，MN＝（AD＋BC）．

（例5）

连接BD，取BD的中点P，连接MP，NP，则MP＝AD，NP＝BC，MP＋NP＝（AD＋BC）＝MN．

∴点P一定在线段MN上，于是AD∥MN，BC∥MN，故AD∥BC．当AD＝BC时，凸四边形是平行四边形；当AD≠BC时，凸四边形是梯形．

例8　如图，过点B作BE∥CA，交DA的延长线于点E，则四边形ACBE为平行四边形，由（1）知BD2－AB2＝AE·AD＝BC·AD．

（例8）

1．（1）72°，72°，108°，108°

（2）3∶5　设大底为a，小底为b，则，化简即可．

2．①③④

3．设CE＝BC＝AD＝x，则x2＋AE2＝x2－52＋112．

4．38．4　过D作DE∥AB，交BC于E，DH⊥BC于H．

5．4或6　如图，过B作BF⊥DA，交DA延长线于F，则四边形BCDF为正方形，又∠ABE＝45°，可证明AE＝CE＋AF．设CE＝x，则DE＝12－x，AF＝10－x，DA＝12－（10－x）＝x＋2．在Rt△ADE中，由102＝（12－x）2＋（x＋2）2，得x1＝4，x2＝6，故CE的长为4或6．

（第5题）

7．D　当14，7为两底时能构成梯形．

8．A

9．C　原直角三角形纸片有两种情况．

10．A　EF＝（BC＋AD），MN＝（BC－AD）．

11．B　设BC＝x，AD＝CD＝y，则2015，且y－1为完全平方数，y＝12＋1，22＋1，…，312＋1，从而P有31个不同的可能值．

12．B　P1（2，0），P2（2，－2），设P2（a2，b2），其中a2＝2，b2＝－2，由对称关系，依次可求得P3（－4－a2，－2－b2），P4（2＋a2，4＋b2），P5（－a2，－2－b2），P6（4＋a2，b2）．令P6（a6，b2），同样可求得点P10的坐标为（4＋a6，b2），即P10（4×2＋a2，b2）．因2010＝4×502＋2，故P2010的坐标为（2010，－2）．

13．（1）（2）

14．连接DM，AM，延长DM交AB的延长线于P，则S梯形ABCD＝S△ADP＝2S△ADM＝2××AD×MN＝MN·AD．

15．过点A作AM⊥BC于点M，过点B作BG⊥BC，与CA的延长线交于点G，则BM＝CM，AG＝CG＝AB，BG＝2AM＝2DF＝BE，

∴∠BGE＝∠BEG＝3∠ABE，得5∠ABE＝90°，∠ABE＝18°，

故∠BAD＝90°＋3×18°＝144°．

16．取BC中点H，连接DH，EH．作HP∥BF，可证明FP＝GP，EP＝DP．

17．如图，过A，D分别作AP，DQ垂直于AD，分别交BC于P，Q，过E，F分别作AD的垂线交AD所在直线于K，N，可证明AP＝DQ＝AK＝DN，JK＝JN．因为EK∥MJ∥FN，所以EM＝MF．

18．将长方形严格分割成9，10，11个等腰梯形的方法如图①、②、③所示，其中α＝67．5°，β＝45°．

（第17题）

（第18题）

这三种分割方法稍加改进，就可以得到将长方形严格分割成12个等腰梯形的方法，如图④．

（第18题）

若已经得到了将长方形严格分割成n个等腰梯形的方法，用图⑤所示策略就可以将长方形严格分割成（n＋4）个等腰梯形．