八年级2020数学第18讲：平行四边形解题思路及示例

1963年，10岁的怀尔斯在英国剑桥弥尔顿路的图书馆被一本名为《大问题》的书吸引住了，它就是引领怀尔斯进入费马大定理的一本书．从1986年至1995年，历经近9年时间，怀尔斯证明了费马大定理，这被认为是20世纪最伟大的数学成果之一．围绕这个看似简单的定理，欧拉、柯西、希尔伯特、图灵、哥德尔、谷山丰、伽罗华，还有最后的怀尔斯，他们前赴后继用了整整三百多年才完成这项证明．

知能概述

平行四边形是一类特殊的四边形，它的特殊性体现在边、角、对角线上，矩形、菱形是特殊的平行四边形，它们既有平行四边形的性质，又有各自特殊的性质．

对角线是解决四边形问题的常用线段，对角线本身的特征又可以决定四边形的形状、大小．连对角线后，平行四边形就产生特殊三角形，因此解平行四边形相关问题时，既要用到全等三角形法、特殊三角形性质，又要善于构造平行四边形，利用平行四边形丰富的性质为解题服务．

熟悉以下基本图形、基本结论：

问题解决

例1　（1）如图①，在矩形ABCD中，已知AD＝12，AB＝5，P是AD边上任意一点，PE⊥BD于点E，PF⊥AC于点F，那么PE＋PF 的值为________．

（全国初中数学联赛题）

在数学中，犹如在诗歌中，同样肯定能找到愉悦的真情．

——罗素

完美矩形

1936年，英国剑桥大学三一学院的学生塔特、斯通、布鲁克斯、史密斯思考这样的问题：把一个矩形分割成边长各不相等的正方形，这样的矩形称为完美矩形，分割成小正方形的个数称为它的阶．四年之后，布鲁克斯率先给出了9阶完美矩形．

（2）如图②，在菱形ABCD中，AB＝4a，E在BC上，BE＝2a，∠BAD＝120°，P点在BD上，则PE＋PC 的最小值为________．

（“希望杯”邀请赛试题）

解题思路　对于（1），△AOD为等腰三角形，若能联想到等腰三角形性质，则问题易解；对于（2），连接AC，由对称性确定P点位置．

例2（1）如图①，在ABCD中，∠ABC＝75°，AF⊥BC于F，AF交BD于E，若DE＝2AB，则∠AED的大小是（　）．

A．60°　B．65°　C．70°　D．75°

（“希望杯”邀请赛试题）

（2）如图②，在菱形ABCD中，△AEF是正三角形，点E，F分别在边BC，CD上，且AB＝AE，则∠B的值为（　）．

A．60°　B．80°　C．100°　D．120°

（安徽省竞赛题）

解题思路　对于（1），作出直角三角形常用辅助线；对于（2），设∠B＝x°，建立关于x的方程．

例3　如图，已知ABCD，以AC为边在两侧各作一个正三角形ACP，ACQ．求证：四边形BPDQ为平行四边形．

（湖北省武汉市竞赛题）

解题思路　可从不同角度判定，而发现图中其他平行四边形是证题的关键．

平行四边形、矩形有以下重要性质，你能证明吗？

（1）如图，已知ABCD，则AC2＋BD2＝2（AB2＋BC2）．

（2）如图，已知P为矩形ABCD内一点，则PA2＋PC2＝PB2＋PD2．

例4　将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG．

（1）如图，当点E在BD上时，求证：FD＝CD；

（2）当α为何值时，GC＝GB？画出图形，并说明理由．

（山东省临沂市中考题）

解题思路　对于（2），由GC＝GB可大致确定G点位置，而在旋转过程中点G与矩形ABCD位置不确定，故需分类讨论．

例5　已知ABCD的周长为28，过顶点D作直线AB，BC的垂线，垂足分别为E，F，若DE＝3，DF＝4．

求：（1）边AB，BC的长；（2）BE＋BF的长．

（天津市“未来之星”数学邀请赛试题）

解题思路　四边形不具有稳定性，符合条件的图形形状唯一吗？解题的关键是分类讨论．

例6　请阅读下列材料：

问题：如图①，在菱形ABCD和菱形BEFG中，点A，B，E在同一条直线上，P是线段DF的中点，连接PG，PC．若∠ABC＝∠BEF＝60°，探究PG与PC的位置关系及的值．

小聪同学的思路是：延长GP交DC于点H，构造全等三角形，经过推理使问题得到解决．

请你参考小聪同学的思路，探究并解决下列问题：

（1）写出上面问题中线段PG与PC的位置关系是________，＝________．

（2）将图①中的菱形BEFG绕点B顺时针旋转，使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上，原问题中的其他条件不变（如图②），你在（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明．

例6设问由易到难，由浅入深，由特殊到一般，前一问为下一问埋下伏笔，梯次递进，不断超越．在解题过程中，我们既展示了聪明才智，又感受了超越自我的乐趣．

（3）若图①中∠ABC＝∠BEF＝2α（0°＜α＜90°），将菱形BEFG绕点B顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出＝________（用含α的式子表示）．

（北京市中考题）

解题思路　在图①中按小聪的思路操作，可得P为DF，GH的中点，又CH＝CG，故PC⊥PG．这种思路能否迁移到图②中？需证明全等三角形．

例7　如图，在△ABC中，∠C＝90°，点M在BC上，且BM＝AC，点N在AC上，且AN＝MC，AM与BN相交于点P，求证：∠BPM＝45°．

（浙江省杭州市竞赛题）

分析与解　条件给出的是线段的等量关系，求证的却是角度等式，由于条件中有直角和相等的线段，因此，可想到等腰直角三角形，解题的关键是平移AN或AC，即作，构造平行四边形．

如图，过M作，连接NE，BE，则四边形AMEN为平行四边形，得NE＝AM，ME⊥BC．

∵ME＝CM，∠EMB＝∠MCA＝90°，BM＝AC，

∴△BEM≌△AMC，得BE＝AM＝NE，∠1＝∠2，∠3＝∠4．

∵∠1＋∠3＝90°，∴∠2＋∠4＝90°且BE＝NE，

∴△BEN为等腰直角三角形，∠BNE＝45°．

∵AM∥NE，∴∠BPM＝∠BNE＝45°．

证明与反驳

美国数学家奥姆斯特德指出：“数学由两类——证明和反例组成，而数学发现也朝着两个主要的目标——提出证明和构造反例．”

反例就是符合题设条件而结论错误的实例．反例需深思才能构造出来，构造反例是说明一个命题不成立的有效方法．

例8　下面有四个命题：

（1）一组对边相等且一组对角相等的四边形是平行四边形；

（2）一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形；

（3）一组对角相等且这一组对角的顶点所连接的对角线平分另一条对角线的四边形是平行四边形；

（4）一组对角相等且这一组对角的顶点所连接的对角线被另一条对角线平分的四边形是平行四边形．

上述命题是否正确？正确的请证明，错误的请举出反例．

（全国初中数学联赛题）

作MEAN，相当于将AN沿着AN的方向平移到ME的位置，这就是平移变换．平移变换前后的对应线段平行且相等，对应角的两边分别平行且相等，通常条件有彼此平行的线段或造成平行的因素，可采用平移变换，这是解平行四边形问题的一个重要技巧．

解　命题（1）是假命题．如图①中的四边形ABCD，它满足命题的条件，∠A＝∠C，AB＝CD，但它不是平行四边形．

命题（2）是假命题．如图②，延长等腰三角形ADE底边ED至任意点O，以O为对角线的交点作ABCE，这时四边形ABCD满足AD＝BC且AO＝OC，但它不是平行四边形．

命题（4）也是假命题，如图③，在四边形ABCD中，∠BAD＝∠BCD，BD垂直平分AC，但四边形ABCD不是平行四边形．

下面证明命题（3）是真命题．如图④，在四边形ABCD中，∠BAD＝∠DCB，且OB＝OD，以O为中心，将△ABD逆时针旋转180°．

因为OB＝OD，所以B与D重合，点A与射线O　C上的点A′（不是C）重合，则∠BA′D＞∠BCD（A′在线段OC上，非点C），或∠BA′D＜∠BCD（A′在线段OC的延长线上）．都与∠BA′D＝∠BAD＝∠BCD矛盾，所以A′即为C，即OA＝OA′＝OC，所以A′即为点C，即OA＝OA′＝OC．所以四边形ABCD是平行四边形．

1．在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合）．对于任意矩形ABCD，下面四个结论中，

①存在无数个四边形MNPQ是平行四边形；

②存在无数个四边形MNPQ是矩形；

③存在无数个四边形MNPQ是菱形；

④至少存在一个四边形MNPQ是正方形．

所有正确结论的序号是________．

（北京市中考题）

2．如图，在Rt△ABC中，CB＝3，CA＝4，M为斜边AB上一动点，过M作MD⊥AC于D点，过M作ME⊥CB于点E，则线段DE的最小值为________．

（四川省竞赛题）

（第2题）

（第3题）

3．如图，在矩形ABCD中，M是边AD的中点，N是边DC的中点，AN与MC交于点P，若∠MCB＝∠NBC＋33°，则∠MPA＝________．

（北京市竞赛题）

4．如图，将两个长为8、宽为2的矩形透明塑料片交叉摆放，重叠部分是菱形ABCD，当两个塑料片垂直时，菱形ABCD的周长有最小值8；当两个塑料片不重合但有一条对角线重合时，菱形ABCD的周长最大，这个最大值是________．

（“希望杯”邀请赛试题）

（第4题）

（第5题）

（第6题）

5．如图，在△ABC中，AB＝3，AC＝4，BC＝5，△ABD，△ACE，△BCF都是等边三角形，则四边形AEFD 的面积为________．

（山东省竞赛题）

6．如图，在矩形ABCD中，AB＝2，BC＝4，点E，F分别在BC，CD上，若AE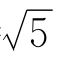＝，∠EAF＝45°，则AF的长为________．

（山东省滨州市中考题）

7．已知四边形ABCD，从下列条件中：①AB∥CD；②BC∥AD；③AB＝CD；④BC＝AD；⑤∠A＝∠C；⑥∠B＝∠D任取其中两个，可以得出“四边形ABCD是平行四边形”这一结论的情况有（　）．

A．4种　B．9种　C．13种　D．15种

（江苏省竞赛题）

8．给出下列命题：①一组对边和一组对角分别相等的四边形是平行四边形；②两组对角的内角平分线分别平行的四边形是平行四边形；③一组对边中点间的距离等于另一组对边长和的一半的四边形是平行四边形；④两条对角线都平分四边形的面积的四边形是平行四边形．其中，真命题有（　）．

A．1个　B．2个　C．3个　D．4个

（湖北省武汉市竞赛题）

9．如图，矩形ABCD的周长是16，DE＝2，△FEC是等腰直角三角形，∠FEC＝90°，则AE的长为（　）．

A．3　B．4

C．5　D．6

（“希望杯”邀请赛试题）

（第9题）

10．已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（5，0），OB＝，点P是对角线OB上的一个动点，D（0，1）．当CP＋DP最短时，点P的坐标为（　）．

（第10题）

（湖北省咸宁市中考题）

11．如图，在ABCD中，BC＝2AB，CE⊥AB于E，F为AD的中点，若∠AEF＝54°，则∠B＝（　）．

A．54°　B．60°　C．66°　D．72°

（湖北省武汉市竞赛题）

（第11题）

（第12题）

（第13题）

12．如图，在菱形ABCD中，已知AB＝3，DF＝1，∠DAB＝60°，∠EFG＝15°，FG⊥BC，则AE＝（　）．

（全国初中数学联赛题）

13．如图，在矩形ABCD中，点M，N，P，Q分别在边AB，BC，CD，DA上，使得S△AQM＝S△BMN＝S△CNP＝S△DPQ．求证：四边形MNPQ为平行四边形．

（伊朗几何奥林匹克试题）

14．如图，在菱形ABCD中，∠BAD＝120°，M为BC上一点，N为CD上一点．求证：若△AMN有一个内角等于60°，则△AMN为等边三角形．

（俄罗斯莫斯科市竞赛题）

（第14题）

（第15题）

（第16题）

15．如图，在六边形ABCDEF中，AB∥DE，BC∥EF，CD∥AF，对边之差BC－EF＝ED－AB＝AF－CD＞0，求证：该六边形的各角相等．

（全俄数学奥林匹克试题）

16．如图，已知八边形所有的角都相等，且边长皆为整数．求证：该八边形对边相等．

（全俄数学奥林匹克试题）

17．如图，菱形PQRS内接于矩形ABCD，使得P，Q，R，S为AB，BC，CD，DA边上的点，已知PB＝15，BQ＝20，PR＝30，QS＝40．若记约分数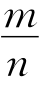为矩形ABCD的周长，求m＋n．

（第17题）

（美国中学生数学邀请赛试题）

18．在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC的延长线于点F．

（第18题）

（1）在图①中证明：CE＝CF；

（2）若∠ABC＝90°，G是EF的中点（如图②），直接写出∠BDG的度数；

（3）若∠ABC＝120°，FG∥CE，FG＝CE，分别连接DB，DG（如图③），求∠BDG的度数．

（北京市中考题）

19．如图，在ABCD中，AE⊥BC，AF⊥CD，H为△AEF三边上的高的交点．求证：AC2＝AH2＋EF2．

（四川省竞赛题）

（第19题）(www.xing528.com)

20．我们知道平行四边形有很多性质．如果我们把平行四边形沿着它的一条对角线翻折，那么会发现这其中还有更多的结论．

发现与证明：

在ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连接B′D．

结论1：B′D∥AC；

结论2：△AB′C与ABCD重叠部分的图形是等腰三角形；

请利用图①证明结论1或结论2（只需证明一个结论）．

应用与探究：

在ABCD中，已知∠B＝30°，将△ABC沿AC翻折至△AB′C，连接B′D．

（第20题）

（1）如图①，若AB　＝，∠AB′D＝75°，则∠ACB＝__________°，BC＝________；

（2）如图②，AB＝，BC＝1，AB′与边CD相交于点E，求△AEC的面积；

（3）已知AB＝，当BC长为多少时，△AB′D是直角三角形？

（江苏省镇江市中考题）

21．△ABC是正三角形，在BC上取点A1，A2，在CA上取点B1，B2，在AB上取点C1，C2，使得凸六边形A1A2B1B2C1C2的边长都相等，如图所示．求证：直线A1B2，B1C2，C1A2相交于一点．

（北京市竞赛题）

（第21题）

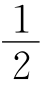例1　（1）作AG⊥BD于G，则PE＋PF＝AG，又AB×AD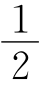＝BD×AG，得PE＋PF＝．

（2）A，C关于BD对称，连接AE交BD于P，且AE⊥BC，∠BAE＝30°，PE＋PC＝AE＝为最小．

例2　（1）B　取DE中点M，连接AM，则AM＝AB．

（2）B　设∠B＝x°，则∠BAE＝∠DAF＝180°－2x°，由x＋2×（180－2x）＋60＝180，得x＝80．

例3　因△ACP与△ACQ都是正三角形，于是PA＝AC＝CQ＝PC＝AQ，故四边形PAQC为平行四边形．连接PQ交AC于O，则O点是AC的中点，也是PQ的中点．

连接BD，因ABCD是平行四边形，故BD与AC互相平分，即BD的中点也是O．

因为PO＝QO，BO＝DO，所以BPDQ为平行四边形．

（例3）

（例4）

例4　（1）由△AEH≌△FDH得AE＝FD＝AB＝CD，即FD＝CD．

（2）画图如图①、图②所示．

当GC＝GB时，点G在BC的垂直平分线上，分两种情况讨论：

①当点G在AD右侧时，如图①，取BC的中点H，连接GH交AD于点M，连接GD，则GH⊥BC，

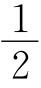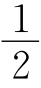∴四边形ABHM是矩形，∴AM＝BH＝AD＝AG．

∴GM垂直平分AD，∴GD＝GA＝DA，

∴△ADG是等边三角形，∴∠DAG＝60°，即α＝60°．

②当点G在AD左侧时，如图②，同理得△ADG是等边三角形，∠DAG＝60°，∴α＝360°－60°＝300°．

例5　（1）AB＝8，BC＝6．

（2）当∠A为锐角时，BE＋BF＝　2＋；当∠A为钝角时，BE＋BF＝　14＋

例6　（1）PG⊥PC，

（例6）

（2）猜想：（1）中的结论没有发生变化．

证明：如图，延长GP交AD于点H，连接CH，CG．

∵P是线段DF的中点，∴FP＝DP．

由题意可知AD∥FG，∴∠GFP＝∠HDP．

∵∠GPF＝∠HPD，∴△GFP≌△HDP．

∴GP＝HP，GF＝HD．

∵四边形ABCD是菱形，∴CD＝CB，∠HDC＝∠ABC＝60°．

由∠ABC＝∠BEF＝60°，且菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上，可得∠GBC＝60°，∴∠HDC＝∠GBC．

∵四边形BEFG是菱形，∴GF＝GB，∴HD＝GB．

∴△HDC≌△GBC，∴CH＝CG，∠DCH＝∠BCG．

∴∠DCH＋∠HCB＝∠BCG＋∠HCB＝120°，即∠HCG＝120°．

∵CH＝CG，PH＝PG，∴PG⊥PC，∠GCP＝∠HCP＝60°．

∴

（3）tan（90°－α）．

1．①②③　2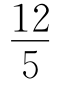．　连接MC，则MC＝DE，当MC⊥AB时，MC值最小．

3．33°　4．17

5．6　四边形AEFD是平行四边形．

6．以下提示供参考：如图，取AD中点M，作MN⊥BC于点N，交AF于点P，连接PE，得到正方形ABNM，BE＝NE＝1，设MP＝x，则PE＝x＋1，PN＝2－x，由（x＋1）2＝（2－x）2＋12得x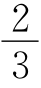＝，DF＝2　MP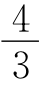＝，故

（第6题）

7．B　8．B　只有②④正确．　9．A

10．D　连接AD，交OB于点P，此时CP＋DP的值最小，B点坐标为（8，4）．

11．D　取BC中点G，连FG，或延长EF，CD交于H点．

12．D　过点F作FH⊥AB于H，△FHE为等腰直角三角形．

13．如图，设AB＝CD＝a，AD＝BC＝b，AM＝x，PC＝y，AQ＝z，NC＝t．若x≠y，不妨设x＞y，则

a－x＜a－y．　①

由S△AQM＝S△CNP得xz＝yt⇒z＜t，

∴b－t＜b－z．　②

由①、②得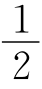（a－x）（b－t）＜（a－y）（b－z），

（第13题）

∴S△BMN＜S△DPQ，

这与题设矛盾，因此，x＝y，类似可证z＝t．

于是，△AMQ≌△CPN⇒MQ＝PN，类似可证MN＝PQ．

从而，四边形MNPQ为平行四边形．

14．如图，连接AC，则易证△ABC与△ADC都为等边三角形．

（1）若∠MAN＝60°，则△ABM≌△ACN．∵AM＝AN，∠MAN＝60°，∴△ANM为等边三角形．

（2）若∠AMN＝60°，过M作CA的平行线交AB于P．∵∠BPM＝∠BAC＝60°，∠B＝60°，∴△BPM为等边三角形，BP＝BM，但BA＝BC，∴AP＝MC，又∠APM＝120°＝∠MCN，∠PAM＝∠AMC－∠B＝∠AMC－60°＝∠AMC－∠AMN＝∠CMN，∴△PAM≌△CMN，∴AM＝MN，又∠AMN＝60°，故△AMN为等边三角形．

（第14题）

（第15题）

（第17题）

15．如图，分别过A点作AM∥EF，过C点作CP∥AB，过E点作EN∥AF，它们分别交于N，M，P点，得，则EF＝AN，AB＝CM，CD＝PE，BC＝AM，AB＝CM，CP＝DE，AF＝NE，由条件得△NMP为等边三角形，可推得六边形的各角均为120°．

16．将八边形向外补形为一个矩形，由矩形对边相等，有，即a5－a1＝（a8＋a2－a6－a4）．

∵ai（i＝1，2，…，8）是整数，而是无理数，则必有a5－a1＝0．

∴a5＝a1．同理可证a6＝a2，a7＝a3，a8＝a4．

17．如图，设AS＝x，AP＝y．由于菱形与矩形都是中心对称图形，故它们的对称中心重合于矩形的中心O，由对称性可知，CQ＝x，CR＝y．

由PR＝30，QS＝40，得PO＝OR＝15，QO＝OS＝20，故△BPQ≌△OPQ，这个矩形被分成了六个边长分别为15，20，25的直角三角形与两个边长分别为x，y，25的直角三角形．

由矩形的面积，可得6×150＋x×y＝（20＋x）×（15＋y）．

化简，得3x＋4y＝120．

由Rt△ASP，得x2＋y2 ＝625．

解由这两个方程组成的联立方程，得x＝20或x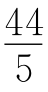＝．但x＝20与PR＝30不符，故舍去．

由x＝，得y＝．

从而矩形ABCD的周长＝，即m＋n＝677．

18．（1）略

（2）∠BDG＝45°．

（3）如图，延长AB至H，使AH＝AD，连接DH，则△AHD是等边三角形．

∵AH＝AD＝DF，∴BH＝GF，

又∠BHD＝∠GFD＝60°，DH＝DF，

∴△DBH≌△DGF，∠BDH＝∠GDF，

∴∠BDG＝∠ADC－∠ADB－∠GDF＝∠ADC－（∠ADB＋∠BDH）＝120°－60°＝60°．

（第18题）

19．连接EH，HF．

∵EH⊥AF，AF⊥CD．

∴EH∥CD．

同理，HF∥BC．

故四边形ECFH是平行四边形．

将△AEH沿HF平移得△A′CF．则点A′在边AD上．于是，AH＝A′F．

故△A′FE为直角三角形，且A′E2＝A′F2＋EF2．

因AE⊥BC，故四边形AECA′为矩形．

从而，AC＝EA′．

故AC2＝AH2＋EF2．

（第19题）

20．发现与证明：

如图①，设AD与B′C相交于点F．

∵△ABC沿直线AC翻折至△AB′C，

∴△ABC≌△AB′C，∠ACB＝∠ACB′，BC＝B′C．

∵四边形ABCD是平行四边形，

∴AD＝BC，AD∥BC，∴B′C＝AD，∠ACB＝∠CAD，

（第20题）

∴∠ACB′＝∠CAD＝，

∴AF＝CF，∴B′F＝DF，∴∠CB′D＝∠B′DA＝．

∵∠AFC＝∠B′FD，∴∠ACB′＝∠CB′D，∴B′D∥AC．

应用与探究：

（1）∠ACB＝45°，BC＝；

（2）如图②，过点C分别作CG⊥AB，CH⊥AB′，

（第20题）

（3）按△AB′D中的直角分类；

①∠B′AD＝90°时，如图③，∠ACB＝30°，BC＝6；

如图④：∠BAC＝30°，BC＝2；

②当∠AB′D＝90°时，如图⑤，∠ACB＝60°，BC＝4；

③当∠ADB′＝90°时，如图⑥，∠ACB＝90°，BC＝3；

综上，BC的长为6，2，4或3时，△AB′D是直角三角形．

（第20题）

21．在正△ABC内作正△PA1A2，连接PB1，PB2，PC1，PC2，如图所示，由C1C2∥PA1，C1C2＝PA1＝A1C1，B1B2∥A2P，B1B2＝A2P＝A2B1，得PA1C1C2，PB1B2C2都是菱形，且△PB2C1是正三角形．

连接A1B1，B1C1，C1A1，注意

∠C1B2B1＝60°＋∠PB2B1＝60°＋∠PA2B1＝∠A1A2B1，

∠A1C2C1＋∠A2B1B2＝∠A1PC1＋∠A2PB2＝360°－60°－60°＝240°．

而∠A1B2B1＋∠A2B1B2＝（∠A2B1C＋∠C）＋（∠B1A2C＋∠C）

＝（∠A2B1C＋∠C＋∠B1A2C）＋60°＝180°＋60°＝240°，

所以∠A1C2C1＝∠A1A2B1，进而∠A1C2C1＝∠A1A2B1＝∠C1B2B1，

因此△B1A2A1≌△C1B2B1≌△A1C2C1，所以A1B1＝B1C1＝C1A1．

直线A1B2，B1C2，C1A2是△A1B1C1三边的中垂线，故直线A1B2，B1C2，C1A2相交于一点．

（第21题）