直角三角形的性质及勾股定理研究

勾股定理具有世界性，几乎所有的文明古国都对它有所研究，勾股定理是数学上证明方法最多的定理，已发表的证法有400余种．

三国时期，赵爽创造了一幅“弦图”，用分、合、移、补的方法证明了勾股定理．2002年在北京召开的国际数学家大会就用这个“弦图”作为会标．

知能概述

直角三角形是一类特殊三角形，有着丰富的性质：角的关系、边的关系、边角关系，这些性质在求线段的长度、证明线段倍分关系、证明线段之间复杂关系等方面有广泛的应用．

代数化、数形结合是运用勾股定理的常用技巧．

熟悉以下基本图形、基本结论：

问题解决

例1　如图，在△ABC中，AB＝BC＝4，AO＝BO，P是射线CO上的一个动点，∠AOC＝60°，则当△PAB为直角三角形时，AP的长为________．

（江西省中考题）

数学的伟大使命在于从混沌中发现秩序．

——坦普·贝尔

寻找规律

下面等式曾引起美国科普大师加德纳的兴趣：

32＋42＝52，

102＋112＋122＝132＋142．

他开始琢磨：如何用一串连续自然数的平方和构造等式？其中有没有规律？

解题思路　运用勾股定理求相关线段的长，因直角三角形直角顶点不确定，故需全面讨论．

例2　如图，在四边形ABCD中，∠B＝135°，∠C＝120°，AB　＝，BC＝　4－，CD＝，则AD边的长为（　）．

（“《数学周报》杯”全国初中数学竞赛题）

解题思路　通过作辅助线，为直角三角形性质的运用创造条件．

例3　如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．

（1）如图①，若∠CAB＝∠CBA＝∠CDE＝∠CED＝50°．

①求证：AD＝BE；

②求∠AEB的度数．

（2）如图②，若∠ACB＝∠DCE＝120°，CM为△DCE中DE边上的高，BN为△ABE中AE边上的高，试证明：

（山东省菏泽市中考题）

解题思路　对于（2），AE＝AD＋DE，迁移问题（1）的解法，寻找线段间的关系．

例4　（1）数学理解：如图①，△ABC是等腰直角三角形，过斜边AB的中点D作正方形DECF，分别交BC，AC于点E，F，求AB，BE，AF之间的数量关系；

（2）问题解决：如图②，在任意直角△ABC内，找一点D，过点D作正方形DECF，分别交BC，AC于点E，F，若AB＝BE＋AF，求∠ADB的度数；

（3）联系拓广：如图③，在（2）的条件下，分别延长ED，FD，交AB于点M，N，求MN，AM，BN的数量关系．

（贵州省贵阳市中考题）

勾股定理在几何中有着极其重要的作用，一些著名问题都可以归结为勾股定理的应用．

（1）中线公式

如图，a，b，c为△ABC的三边长，AD为△ABC中BC边的中线，则AD2＝（2b2＋2c2－a2）．

（2）斯坦纳定理

如图，P为△ABC内任意一点，PD⊥BC于D，PE⊥CA于E，PF⊥AB于F，则AF2＋BD2＋CE2＝AE2＋CD2＋BF2．

解题思路　对于（2），条件AB＝BE＋AF如何运用？对于（3），先猜后证，把一直线上的三条线段集中于一个三角形中是解题的关键．

例5　（1）问题背景：

在△ABC中，AB，BC，AC三边的长分别为，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．

请你将△ABC的面积直接填写在横线上：________．

（2）思维拓展：

我们把上述求△ABC面积的方法叫作构图法，若△ABC三边的长分别为，请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．

（3）探索创新：

若△ABC三边的长分别为（m＞0，n＞0，且m≠n），试运用构图法求出这个三角形的面积．

（湖北省咸宁市中考题）

解题思路　由数到形，的几何意义是直角边为a，b的直角三角形斜边的长，这是解本例的关键．

例6　一个直角三角形的边长都是整数，它的面积和周长的数值相等，这样的直角三角形是否存在？若存在，确定它的三边长；若不存在，说明理由．

（北京市竞赛题）

在运用勾股定理时，常需对a2＋b2＝c2进行变形，运用乘法公式、整数与方程知识综合求解．

例5、例6充分体现了勾股定理运用中的数形结合思想．

分析与解　假设存在符合条件的直角三角形，它的三边长为a，b，c，其中c为斜边，则于是将存在性问题的讨论转化为求方程组的解．由于a，b，c均为正整数，所以a≠b，不妨设a＞b，则有，两边平方整理得，，消去ab，得，即（a－4）（b－4）＝8＝1×8＝2×4　∴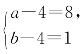或分别得a＝12，b＝5，c＝13；a＝8，b＝6，c＝10．

弦　图

如图①中边长为a，b，c的四个全等的直角三角形可以拼成如图②所示的图形，这个图形被称为“弦图”，由图①及弦图你能写出若干等式吗？

例7　阅读下面材料：

小明遇到这样一个问题：如图①，在边长为a（a＞2）的正方形ABCD各边上分别截取AE＝BF＝CG＝DH＝1，当∠AFQ＝∠BGM＝∠CHN＝∠DEP＝45°时，求正方形MNPQ的面积．

小明发现，分别延长QE，MF，NG，PH交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE四个全等的等腰直角三角形（如图②）．请回答：

（1）若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙不重叠），则这个新正方形的边长为________；

（2）求正方形MNPQ的面积．

参考小明思考问题的方法，解决问题：

如图③，在等边△ABC各边上分别截取AD＝BE＝CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ，若S△RPQ＝，则AD的长为________．

（北京市中考题）

赵爽，汉末三国初数学家．

赵爽的无字证明简洁而极富创意，他用几何图形的截、割、拼、补来证明代数恒等式，严密又直观，为中国古代“形数统一”、代数和几何紧密结合的独特风格树立了典范，更具有科学创新的重大意义．

解题思路　问题（1）为问题（2）的解决提供了可以借鉴的方法，而解问题（3）需逆向思考，由面积求相关线段．

1．（1）Rt△ABC三边的长分别是x，x＋1和5，则△ABC的周长＝________，△ABC的面积＝________．

（“希望杯”邀请赛试题）

（2）以200912为一条直角边，且三条边都是整数的不同的直角三角形（全等三角形视为同一三角形）有________个．

（青少年数学国际城市邀请赛试题）

2．如图，在四边形ABCD中，对角线AC平分∠BAD，AB＝21，AD＝9，BC＝CD＝10，则AC＝________．

（“希望杯”邀请赛试题）

（第2题）

（第3题）

（第4题）

3．如图，已知Rt△ABC的两直角边AC＝5，BC＝12，AD平分∠CAB，则CD＝________．

（山西省太原市竞赛题）

4．如图，在等腰Rt△ABC中，AB＝BC＝5，P是△ABC内一点，且PA＝，PC＝5，则PB＝________．

（全国初中数学联赛题）

5．如图，AB与CD相交于点O，AB＝CD，∠AOC＝60°，∠ACD＋∠ABD＝210°，则线段AB，AC，BD之间的等量关系式为________．

（第5题）

（广西壮族自治区中考题）

6．长方形ABCD中嵌入了如图所示的5个相同的正方形和一个三角形，E，F，G，H分别在长方形的边AB，BC，CD和DA上．已知AB＝22米，BC＝20米，则嵌入的图形总面积为________．

（第6题）

（“华罗庚金杯”少年数学邀请赛试题）

7．设一直角三角形的两条直角边为a，b，斜边为c，斜边上的高为h，那么以c＋h，a＋b，h为边构成的三角形的形状是（　）．

A．直角三角形

B．锐角三角形

C．钝角三角形

D．不能确定，形状与a，b，c大小有关

（“祖冲之杯”竞赛题）

8．对如下的三个命题：

命题1：边长为连续整数的直角三角形是存在的．

命题2：边长为连续整数的锐角三角形是存在的．

命题3：边长为连续整数的钝角三角形是存在的．

正确命题的个数为（　）．

A．0　B．1　C．2　D．3

（江苏省竞赛题）

9．在直角三角形中，三条边的长均为整数，分别记为a，b，c，其中c为斜边长．若c＝－（a＋b），则符合条件的直角三角形有（　）个．

A．3　B．4　C．6　D．12

（“华罗庚金杯”少年数学邀请赛试题）

10．如图，在△ABC中，AB＝AC＝4，P是BC上异于B，C的一点，则AP2＋BP·PC的值是（　）．

A．16　B．20

C．25　D．30

（第10题）

（“希望杯”邀请赛试题）

11．如图，在△ABC中，∠C＝90°，∠BAC＝60°，AC＝1，点D在BC上，点E在AB上，使得△ADE是等腰直角三角形，∠ADE＝90°，则BE长度为（　）．

（全国初中数学联赛题）

（第11题）

（第12题）

（第13题）

12．如图，设△ABC满足下面条件：AB＝AC，又D是AC上一点，且使BD⊥AC，而AD，CD长是整数且BD2＝57．在所有这类三角形中最小的AC的值是（　）．

A．9　B．10　C．11　D．12　E．13

（美国数学邀请赛试题）

13．如图，过△ABC内一点P做三边的垂线，垂足分别为D，E，F，已知AB＝5，BC＝7，AC＝6，BE－AD＝1，求AD＋BE＋CF．

（全国初中数学联赛题）

三边长为连续整数且面积也为整数的三角形存在吗？如果存在，有多少个？(www.xing528.com)

这是一个古老的问题，这种三角形又叫海伦三角形，第8题从一个侧面给出了上述问题的答案．

14．如图，自△ABC内的任一点P，作三角形三条边的垂线：PD⊥BC，PE⊥CA，PF⊥AB，若BD＝BF，CD＝CE，求证：AE＝AF．

（江西省竞赛题）

（第14题）

（第15题）

15．如图，在四边形ABCD中，∠ABC＝30°，∠ADC＝60°，AD＝CD，求证：BD2＝AB2＋BC2．

（北京市竞赛题）

16．如图，在Rt△BCD中，∠CBD＝90°，BC＝BD，点A在CB的延长线上，且BA＝BC，点E在直线BD上移动，过点E作射线EF⊥EA，交CD所在直线于点F．

（1）当点E在线段BD上移动时，如图①所示，求证：BC－DE＝DF．

（2）当点E在直线BD上移动时，如图②③所示，线段BC，DE与DF又有怎样的数量关系？请直接写出你的猜想，不需要证明．

（第16题）

（黑龙江省中考题）

17．设a，b，c，d为正实数，a＜b，c＜d，bc＞ad，有一个三角形的三边长分别为，求此三角形的面积．

（“五羊杯”竞赛题）

18．边长为连续的自然数且周长不超过2010的锐角三角形有多少个？

（世界数学团体锦标赛试题）

19．定义：三边长和面积都是整数的三角形称为“整数三角形”．数学学习小组的同学从32根等长的火柴棒（每根长度记为1个单位）中取出若干根，首尾依次相接组成三角形，进行探究活动．

小亮用12根火柴棒，摆成如图所示的“整数三角形”；

小颖分别用24根和30根火柴棒摆出直角“整数三角形”；

（第19题）

小辉受到小亮、小颖的启发，分别摆出三个不同的等腰“整数三角形”．

（1）请你画出小颖和小辉摆出的“整数三角形”的示意图；

（2）你能否也从中取出若干根，按下列要求摆出“整数三角形”？如果能，请画出示意图；如果不能，请说明理由．

①摆出等边“整数三角形”；

②摆出一个非特殊（既非直角三角形，也非等腰三角形）“整数三角形”．

（福建省宁德市中考题）

20．已知直角三角形的边长为整数，周长为30，求它的斜边长．

（全国初中数学联赛题）

21．解方程：

（加拿大数学竞赛题）

例1　2或或如图，当∠AP1B＝90°，△AOP1为等边三角形，AP1＝AO＝2；当∠AP2B＝90°，△BOP2为等边三角形，AP2＝；当∠ABP3＝90°，AP3＝

（例1）

（例2）

例2　D　如图，过A，D分别作AE，DF垂直于直线BC，E，F为垂足．由条件得DF＝，于是过点A作AG⊥DF于G，AD＝

例3　（1）①由△ACD≌△BCE，得AD＝BE．　②∠AEB＝80°．

（2）仿（1）可得AD＝BE，

AE＝DE＋AD＝DE＋BE＝2DM＋BE＝

例4　（1）AB＝

（2）∵四边形DECF是正方形，∴DF＝DE，

将△ADF以点D为旋转中心，逆时针旋转90°得到△A′DE，如图①．

∴AD＝A′D，AF＝A′E，且∠ADA′＝90°，

∵AB＝BE＋AF，∴AB＝BE＋A′E＝A′B，

∴△ABD≌△A′BD，∴∠ADB＝∠A′DB，

∴∠ADB＝

（例4）

（3）由（2）得，AD，BD分别是∠CAB和∠CBA的角平分线，

∴∠MAD＝∠FAD，∠NBD＝∠EBD，

分别延长ED，FD，交AB于点M，N，如图②．

∴EM∥CA，FN∥CB，

∴∠MDA＝∠FAD，∠NDB＝∠EBD，

∴∠MDA＝∠MAD，∠NDB＝∠NBD，

∴AM＝MD，ND＝BN，

在Rt△MDN中，MN2＝MD2＋ND2，

∴MN2＝AM2＋BN2．

（例4）

例5　（1）

（2）△ABC如图①所示（位置不唯一），

（3）构造△ABC如图②所示，

（例5）

例7　（1）a

（2）由（1）可知，由△RQF，△SMG，△TNH，△WPE拼成的新正方形的面积与正方形ABCD的面积相等．

∴△RAE，△SBF，△TCG，△WDH这四个全等的等腰直角三角形的面积之和等于正方形MNPQ的面积．

∵AE＝BF＝CG＝DH＝1，

（例7）

∴正方形MNPQ的面积S＝4××1×1＝2．

分别延长RD，CA，交于T点，可证得△TAD，△TRF均为等腰三角形．三个△TRF可拼成一个等边△ABC，S△RPQ＝3S△TAD，进而可得AD＝．

1．（1）12或30，6或30

（2）612　设（c－a）（c＋a）＝200924＝4124×748，因c＋a＞c－a，且均为奇数，故有25×49个因子，可以配成＝612对因子构成一种可能的解．

2．17

3．　作DE⊥AB于E．

4．作PE⊥AB于E，PF⊥BC于F，设PE＝m，PF＝n，则，（5－m）2＋n2＝52．解得（m，n）＝（1，3），（2，4），当m＝2，n＝4时，PE＞AE，舍去．PB＝

5．AB2＝AC2＋BD2　平移CD至AM，连接BM，DM，则△ABM为等边三角形，∠BDM＝360°－210°－60°＝90°．

6．220平方米　如图，可以将每个正方形依长方形的长与宽的方向构造成“弦图”，显然，所有的直角三角形都相同．设它的直角边为a与b，

从图可知，解得a＝6，b＝2．

每个正方形的面积等于a2＋b2＝36＋4＝40（平方米），而其中三角形面积为正方形的一半，为20平方米．

综上所述，嵌入图形的总面积是40×5＋20＝220（平方米）．

7．A

8．D　边长为3，4，5；4，5，6；2，3，4的三角形显然存在，且分别为直角、锐角、钝角三角形．

9．C　由得（a－12）（b－12）＝72．

（第6题）

10．A　过A作AD⊥BC于D，可证得AP2＋BP·PC＝AB2．

11．A　仅供参考：过点E作EF⊥BC于点F，设CD＝EF＝x，则

12．C　设AD＝m，DC＝n．（m＋n）2－m2＝57，n（2m＋n）＝57＝3×19＝1×57，解得（m，n）＝（8，3），（28，1），m＋n的最小值为11．

13．设AD＝x，BE＝y，CF＝z，则BD＝5－x，CE＝7－y，AF＝6－z．

连接PA，PB和PC，

在Rt△PBD和Rt△PBE中，由勾股定理可得BD2＋PD2＝PB2＝BE2＋PE2，即

（5－x）2＋PD2＝y2＋PE2，

同理可得（7－y）2＋PE2＝z2＋PF2，（6－z）2＋PF2＝x2＋PD2．

将以上三式相加，得（5－x）2＋（7－y）2＋（6－z）2＝x2＋y2＋z2，所以5x＋7y＋6z＝55．

又由已知条件得y－x＝BE－AD＝1，于是可得

AD＋BE＋CF＝x＋y＋z＝［（5x＋7y＋6z）－（y－x）］＝（55－1）＝9．

（第13题）

14．注意以下事实：若四边形的两条对角线互相垂直，则其两组对边的平方和相等．连接PA，PB，PC，则有PA2＋PF2＝PB2＋AF2；PB2＋CD2＝PC2＋BD2；PC2＋AE2＝PA2＋CE2．

三式相加得AE2＋CD2＋BF2＝AF2＋CE2＋BD2，利用条件BD＝BF，CD＝CE，代入上式得AE＝AF．

15．连接AC，则△ADC为等边三角形，以BC为边向外作等边三角形BCE，证明BD＝AE．

（第16题）

（第17题）

18．设三角形三边的长分别为n－1，n，n＋1，则

解得2＜n≤670．

其中，锐角三角形三边的长还要满足（n－1）2＋n2＞（n＋1）2，解得n＞4．

∴4＜n≤670，从而知这样的锐角三角形有666个．

19．（1）小颖摆出如图①所示的“整数三角形”：

（第19题）

小辉摆出如图②所示的三个不同的等腰“整数三角形”：

（第19题）

（2）①不能摆出等边“整数三角形”，理由略．

②摆出如图③所示的一个非特殊“整数三角形”．

20．设直角三角形三边长分别为a，b，c（a≤b＜c），则a＋b＋c＝30，

由a≤b＜c得30＝a＋b＋c＜3c，∴c＞10，

由a＋b＞c得30＝a＋b＋c＞2c，∴c＜15，

∵c为整数，∴11≤c≤14．

∵a2＋b2＝c2，把c＝30－a－b代入并化简得ab－30（a＋b）＋450＝0，

∴（30－a）（30－b）＝450＝2×32×52．

（第21题）