等边三角形的性质和特点，科克雪花曲线

画一个边长为1的正三角形，然后在每边再画一个边长为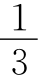的小正三角形，按上述方法，重复画出越来越小的正三角形．左图是瑞典数学家科克于1904年创造出的一种用几何图形描述雪花的方法，人们把它叫作“科克雪花曲线”，它具有无穷大的周长和有限的面积．

知能概述

等边三角形是特殊的等腰三角形，它的特殊性体现在边、角、对称性，以及如下性质：等边三角形内任意一点到三边的距离和是一个定值，等于一边上的高．

利用特殊角或线段构造等边三角形，进而运用等边三角形的性质为解题服务是解相关问题的常用技巧．

熟悉以下基本图形、基本结论：

问题解决

例1　如图，已知六边形ABCDEF的各个内角等于120°，AB＋AF＝5，AF＋FE＝6，AB＝CD，则六边形ABCDEF 的周长为________．

（重庆市竞赛题）

实验、坚持不懈、试错、冒险、即兴发挥、最佳途径、迂回前进……随机应变，所有这些都有助于应付变化．

——卡尔·韦克

莫利定理

将任意三角形的内角三等分，则与每边相邻的两条三等分线的交点构成一个等边三角形．

这一结论由著名数学家莫利发现，被誉为自欧几里得以来所发现的最为优美的定理．

解题思路　通过向外补形，把六边形问题转化为三角形或四边形问题加以解决．

例2　如图，等边△ABC的边长为4，点O是△ABC的中心，∠FOG＝120°，绕点O旋转∠FOG，分别交线段AB，BC于点D，E两点，连接DE，给出下列四个结论：①OD＝OE；②S△ODE＝S△BDE；③四边形ODBE的面积始终等于；④△BDE周长的最小值为6．上述结论中正确的个数是（　）．

A．1　B．2　C．3　D．4

（山东省德州市中考题）

解题思路　四边形ODBE是一特殊四边形，这是解题的基础；对于④，代数化或关注特殊情形．

例3　如图，△ABC中，∠B＝60°，延长BC到D，延长BA到E，使AE＝BD，连CE，DE，若CE＝DE，求证：△ABC是等边三角形．

（“希望杯”邀请赛试题）

解题思路　只需证明AB＝CB．条件AE＝BD，CE＝DE能导出什么结论？延长BD至F，使DF＝BC．

例4　（1）已知：△ABC是等腰三角形，其底边是BC，点D在线段AB上，E是直线BC上一点，且∠DEC＝∠DCE，若∠A＝60°（如图①）．求证：EB＝AD；

（2）若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其他条件不变（如图②），（1）的结论是否成立？并说明理由；

（3）若将（1）中的“若∠A＝60°”改为“若∠A＝90°”，其他条件不变，则的值是多少？

对于比较困难的几何问题，需要把分散的条件加以集中，使隐含的条件加以显现，通过简单的几何变换，常可以达到转化的目的．

判定等边三角形的基本思路有：

（1）从边入手；

（2）从角入手；

（3）从边、角入手．

（直接写出结论，不要求写解答过程）

（山东省泰安市中考题）

解题思路　对于（1），通过作辅助线，构造全等三角形；把解决（1）的方法恰当迁移至问题（2）、（3）是解题的关键．

例5　已知：等边△ABC的边长为a．

探究1　如图①，过等边△ABC的顶点A，B，C依次作AB，BC，CA的垂线围成△MNG．

求证：△MNG是等边三角形且；

探究2　在等边△ABC内取一点O，过点O分别作OD⊥AB，OE⊥BC，OF⊥AC，垂足分别为D，E，F．

（1）如图②，若点O是△ABC的重心，我们可利用三角形面积公式及等边三角形性质得到两个正确结论（不必证明）：

结论1　OD＋OE＋OF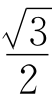＝a；

结论2　AD＋BE＋CF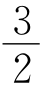＝a．

（2）如图③，若点O是等边△ABC内任意一点，则上述结论1，2是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由．

分析与解　探究1的结论对于探究2的结论2起到了提示作用，构造等边三角形将AD＋BE＋CF转化为OD＋OE＋OF的情形．

图④

例5揭示了等边三角形的几个重要性质．

如图，已知△ABC为等边三角形，O为其内任意一点，OD⊥AB于D，OE⊥BC于E，OF⊥AC于F，则：

（1）OD＋OE＋OF为一定值；

（2）AD＋BE＋CF＝，为定值；

（3）S△ADO＋S△BEO＋S△CFO＝，为定值．

你有不同于例5的证法吗？

探究1　略

探究2　结论1，2仍然成立．证明如下：

如图④，过点A，B，C依次作边AB，BC，CA的垂线围成△MNG，则△MNG为等边三角形且MN＝，过点O分别作OD′⊥MN于D′，OE′⊥NG于E′，OF′⊥MG于F′，由结论得OD′＋OE′＋OF′＝

又四边形ADOF′为矩形，∴OF′＝AD．

同理OD′＝BE，OE′＝CF．

∴AD＋BE＋CF＝OF′＋OD′＋OE′＝

例6　如图，在等腰△ABC中，AB＝AC，顶角A＝20°，在边AB上取点D，使AD＝BC，求∠BDC的度数．

（“祖冲之杯”竞赛题）

分析　虽然80°，20°，80°并不是特殊角，但是它们的差却为60°，60°使我们联想到等边三角形，由此找到解题突破口．

解法1　如图①，以BC边为边在△ABC内作等边△BCO，连AO，由图形的轴对称知，△ABO≌△ACO．

∴∠BAO＝∠CAO＝10°，∠ABO＝20°，∠AOB＝∠AOC＝150°．

又BO＝BC＝AD，

∴△ACD≌△BAO，

∴∠ADC＝∠AOB＝150°．

∴∠BDC＝30°．

图①

解法2　如图②，以AC为边作等边△ACE，连DE，则∠BAE＝80°，AC＝AE＝CE．

∵AD＝BC，∠B＝∠DAE＝80°，

AB＝AC＝AE，

∴△ADE≌△BCA，

∴∠AED＝20°，∠ADE＝80°，

∴AE＝DE＝EC，∠DEC＝60°－20°＝40°，

∴∠CDE＝70°，∠ADC＝80°＋70°＝150°，

∴∠BDC＝30°．

图②

旋转图形

因等边三角形有丰富的性质，故恰当旋转等边三角形（通常旋转60°），可使分散的条件加以集中．

例7　如图，P为等边三角形ABC内的一点，且P到三个顶点A，B，C的距离分别为3，4，5，求△ABC的面积．

分析与解　由3，4，5想到勾股数，怎样使它们集中于一个三角形，这是解题的关键，不妨实施旋转变换，而确定旋转对象需三思．

解几何题，一些特殊的数量（如30°，45°，60°，90°，120°，150°等）能引起我们对重要知识的联想，进而构造相应的图形，这是解特殊三角形、特殊四边形有关问题的一个常用技巧．

例6正是充分注意到已知条件中的数量关系，通过构造等边三角形、全等三角形而顺利求解的．

构造等边三角形的常见方式是：

（1）在等腰三角形的基础上构造；

（2）在60°角的基础上构造；

（3）在已知的角与60°有关联时构造．

波利亚曾说：“拿一个有意义又不复杂的题目去帮助学生发掘问题的各个方面，使得通过这道题就好像通过一道门户，把学生引入一个完整的领域．”

1．如图，D为等边△ABC内一点，BD＝DA，BE＝AB，∠DBE＝∠DBC，则∠BED 的度数是________．

（河南省竞赛题）

（第1题）

（第2题）

（第3题）

2．如图，等边△ABC内有一点P，分别连接AP，BP，CP．若AP＝6，BP＝8，CP＝10，则S△ABP＋S△ACP ＝________．

（四川省巴中市中考题）

3．如图，AC，BD在AB的同侧，AC＝2，BD＝8，AB＝8，点M为AB的中点，若∠CMD＝120°，则CD 的最大值为________．

（湖北省黄冈市中考题）

4．如图，一个六边形的六个内角都是120°，连续四边的长依次是1，3，3，2，则该六边形的周长为________．

（“祖冲之杯”竞赛题）

5．如图，在△ABC中，已知∠CAB＝60°，D，E分别是边AB，AC上的点，∠AED＝60°，ED＋DB＝CE，∠CDB＝2∠CDE，则∠DCB＝________．

（全国初中数学联赛题）

（第4题）

（第5题）

（第6题）

6．如图，P是等边△ABC内部一点，∠APB，∠BPC，∠CPA的大小之比是5∶6∶7，则以PA，PB，PC为边的三角形的三个角的大小之比（从小到大）是（　）．

A．2∶3∶4　B．3∶4∶5

C．4∶5∶6　D．不能确定

数学爱好者、法国数学的早期推动者拿破仑在南征北战的军事行动中，身边总是簇拥着数学家、科学家．他在数学上有较深造诣，时常与学者讨论科学问题，甚至出“难题”．

如下图，取一个三角形，在其边上向外各作一个等边三角形，此时这三个新的三角形的中心又形成一个等边三角形．

传说是拿破仑发现了这一定理，史称“拿破仑三角形”．

7．如图，在四边形ABCD中，AC，BD是对角线，△ABC是等边三角形，∠ADC＝30°，AD＝3，BD＝5，则CD的长为（　）．

（全国初中数学联赛题）

（第7题）

（第8题）

（第9题）

8．如图，设△ABC和△CDE都是正三角形，且∠EBD＝62°，则∠AEB的度数是（　）．

A．124°　B．122°　C．120°　D．118°

（四川省竞赛题）(www.xing528.com)

9．以锐角△ABC的各边为长，在△ABC形外分别作等边三角形，得△ABD，△BCE，△CAF，结论：

①AE＝BF＝CD；

②AE，BF，CD交于一点；

③AE，BF，CD每两条夹角（锐角）都等于60°．

正确选项是（　）．

A．①②③都不成立　B．①②③都成立

C．①③成立，②不成立　D．①成立，②③不成立

10．如图，一个凸六边形的六个内角都是120°，六条边的长分别为a，b，c，d，e，f，则下列等式中成立的是（　）．

A．a＋b＋c＝d＋e＋f　B．a＋c＋e＝b＋d＋f

C．a＋b＝d＋e　D．a＋c＝b＋d

（“希望杯”邀请赛试题）

（第10题）

（第11题）

11．如图，已知四边形ABCD中，AB＝AD，∠BAD＝60°，∠BCD＝120°，求证：BC＋DC＝AC．

（湖北省黄冈市竞赛题）

12．如图，已知等边△ABC，在AB上取点D，在AC上取点E，使得AD＝AE，作三个等边三角形PCD，QAE和RAB，求证：P，Q，R是等边三角形的三个顶点．

（第12题）

（江苏省竞赛题）

13．如图，在△ABC中，AD为BC边上的中线，E是线段AD上一点，且AE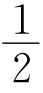＝BC，BE的延长线交AC于F．若AF＝EF，求∠ADB的度数．

（日本数学竞赛题）

（第13题）

（第14题）

（第15题）

14．如图，在△ABC中，∠BAC＝∠BCA＝44°，M为△ABC内一点，使得∠MCA＝30°，∠MAC＝16°．求∠BMC的度数．

（北京市竞赛题）

15．如图，P为△ABC内部一点，使得∠PBC＝30°，∠PBA＝8°，且∠PAB＝∠PAC＝22°，求∠APC的度数．

（青少年数学国际城市邀请赛试题）

16．（1）操作发现：

如图①，D是等边△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边△DCF，连接AF．你能发现线段AF与BD之间的数量关系吗？并证明你发现的结论．

（第16题）

（2）类比猜想：

如图②，当动点D运动至等边△ABC边BA的延长线上时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？

（3）深入探究：

①如图③，当动点D在等边△ABC边BA上运动时（点D与点B不重合），连接DC，以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′，连接AF，BF′，探究AF，BF′与AB有何数量关系？并证明你探究的结论．

②如图④，当动点D在等边三角形边BA的延长线上运动时，其他作法与图③相同，①中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．

（湖南省岳阳市中考题）

17．如图，在△ABC中，∠ABC＝60°，∠ACB＝40°，P为∠ABC的平分线与∠ACB的平分线的交点，求证：AB＝PC．

（第17题）

（北京市竞赛题）

18．（1）发现：

如图①，点A为线段BC外一动点，且BC＝a，AB＝b．填空：当点A 位于________时，线段AC的长取得最大值，且最大值为________（用含a，b的式子表示）．

（2）应用：

点A为线段BC外一动点，且BC＝3，AB＝1．如图②所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．

①请找出图中与BE相等的线段，并说明理由；

②直接写出线段BE长的最大值．

（3）拓展：

如图③，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA＝2，PM＝PB，∠BPM＝90°．请直接写出线段AM长的最大值及此时点P的坐标．

（第18题）

（河南省中考题）

例1　17　如图，延长AB，CD，EF交于P，Q，R，显然△PBC，△AQF，△DER，△PQR都是等边三角形．设六边形ABCDEF的各边依次是a，b，c，d，e，f，由已知，a＋f＝5，f＋e＝6，a＝c，因△PQR是等边三角形，于是有a＋b＋f＝b＋c＋d＝e＋d＋f．可算出a＝5－f，b＝1＋f，c＝5－f，d＝f，e＝6－f，于是a＋b＋c＋d＋e＋f＝17．

（例1）

（例2）

例2　C　连接OB，OC，△DOB≌△EOC．OD＝OE，BD＝CE，S△OBC＝S四边形ODBE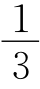＝S△ABC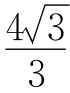＝．当∠FOG绕点O旋转到使OF⊥AB，OG⊥BC时，如图，计算得S△ODE≠S△BDE，△BDE的周长＝BD＋BE＋DE＝CE＋BE＋DE＝BC＋DE＝4＋DE，要使△BDE的周长最小，则DE的长最小，此时BD＝BE＝DE＝2．

例3　延长BD至F，使DF＝BC，连EF，则△BCE≌△FDE，EB＝EF．

∵∠B＝60°，∴△EBF为等边三角形，∴EB＝FB．

∵AE＝BD，BD＝CF，∴AE＝CF．∴AB＝CB，故△ABC为等边三角形．

例4　（1）过点D作DF∥BC交AC于点F，证明△DBE≌△CFD，得EB＝DF＝AD．

（2）方法不变，（1）中结论仍成立．

（3）同理作DF∥BC交AC于点F，

例7　在同一平面内，将△PBC绕点B逆时针旋转60°至△DBA，如图所示：

∵PA＝3，PB＝4，PC＝5，

∴DB＝PB＝4，DA＝PC＝5．

∴△DBP是等边三角形．

∴∠DPB＝60°，PD＝4．

在△ADP中，

∵PA2＋PD2＝32＋42＝25＝AD2，

∴∠APD＝90°，∠APB＝150°．

过点B作BE⊥AP交AP的延长线于点E，易知∠BPE＝30°，

（例7）

1．30°

2．把△ABP绕点A逆时针旋转60°到△AP′C，连接PP′，则原式＝S四边形APCP′＝S△APP′＋S△PCP′．

3．14　如图，将△CAM沿CM翻折至△CA′M，将△DBM沿DM翻折至△DB′M，连接A′B′，则△A′MB′为等边三角形，CD≤CA′＋A′B′＋B′D，当C，A′，B′，D四点共线时，CD有最大值，CD的最大值为CA′＋A′B′＋B′D＝2＋4＋8＝14．

（第3题）

4．15

5．20°　延长DB至F，使BF＝ED，连接CF，则△AED，△ACF都为等边三角形，可证明△CAD≌△CFB，∠ACD＝∠BCF＝20°．

6．A　将△ABP绕B点顺时针旋转60°，得△CBD，则△ABP≌△CBD，△PBD为等边三角形．

7．B　以CD为边作等边△CDE，连接AE，可证明△BCD≌△ACE．

8．B　△BCD≌△ACE，则∠DCB＝∠ECA，设∠BAE＝α，则∠CBD＝∠CAE＝60°－α，∠EBC＝∠EBD－∠CBD＝2°＋α，于是∠EBA＝60°－（2°＋α）＝58°－α，故∠AEB＝180°－α－（58°－α）＝122°．

9．B　OA平分∠DOF，OE平分∠BOC，A，O，E在一条直线上．

10．C

11．延长BC至E，使CE＝CD，连BD，DE，则△DCE，△ABD都是等边三角形，∴DE＝DC，DB＝DA．∵∠BDE＝60°＋∠BDC＝∠ADC，∴△BDE≌△ADC，∴BE＝AC，故BC＋CD＝AC．

12．连接BP，可证明△ADC≌△BPC，又∠RAB＋∠BAC＋∠QAE＝180°，∴R，A，Q三点共线．

∵∠CBP＝∠CAD＝60°，∠RBA＋∠ABC＋∠CBP＝180°，∴R，B，P三点共线，而AQ＝AE＝AD＝BP，∴BQ＝RA＋AQ＝RB＋BP＝RP，又∠R＝60°，故△PQR是等边三角形．

13．下面解法仅供参考：

如图，延长AD至G，使DG＝AE，于是AD＝EG，连BG，则△ACD≌△EBG，

（第13题）

∴BG＝CD＝BD＝AE＝DG．

于是△BDG为正三角形，∴∠ADC＝60°．

故∠ADB＝120°．

14．以下解法仅供参考：

如图，以AC为一边，向点B所在的一侧作等边△ACN，连接BN．

（第14题）

∵△ACN是等边三角形，

∴∠ACN＝∠ANC＝∠CAN＝60°；AC＝AN＝CN．

根据边边边定理有△ABN≌△CBN．

∴∠ANB＝∠BNC＝30°＝∠ACM．

又∠BAN＝∠NAC－∠BAC＝16°＝∠CAM，

根据角边角定理有△ABN≌△AMC，

得AB＝AM，∠ABM＝＝76°，∠CBM＝16°，故∠BMC＝150°．

15．如图，延长AC至点Q，使得AQ＝AB，则△BAP≌△QAP，又∠APB＝180°－∠PBA－∠PAB＝150°，则∠BPQ＝360°－∠APB－∠APQ＝60°．

因此，△BPQ是一个等边三角形，BC是PQ上的中垂线，即∠CPQ＝∠CQP＝∠PBA＝8°，故∠APC＝∠APQ－∠CPQ＝142°．

（第15题）

16．（1）、（2）皆有AF＝BD．

（3）①AB＝AF＋BF′．　②AB＝AF－BF′．

17．如图，以PC为边作等边△PDC，连接AP，AP平分∠BAC，可证明A，P，D三点共线，△ABC≌△CDA，故AB＝CD＝PC．

18．（1）CB的延长线上，a＋b

（2）①DC＝BE．　②BE长的最大值为4．

（3）如图①，构造△BNP≌△MAP，则NB＝AM．由（1）知，当点N在BA的延长线上时，NB有最大值，如图②，易得

（第17题）

∴AM＝NB＝

过点P作PE⊥x轴于点E，则

∴

（第18题）