第15讲等腰直角三角形的解题方法

螺线既是一种迷人的数学现象，又是一种与生命相关的极为普遍的数学形态，其广泛出现在动植物中．瑞士数学家伯努利曾深入研究对数螺线性质，他在遗嘱里吩咐要把对数螺线刻在自己的墓碑上，并附上一语双关的美妙颂词：“虽然改变了，但我还是和原来一样．”

知能概述

等腰三角形的丰富性质为角度的计算、线段相等、直线位置关系的证明等问题提供了新的理论依据．

恰当地构造等腰三角形是解与等腰三角形相关问题的常用技巧，而分类讨论是解等腰三角形问题的重要方法．

熟悉以下基本图形、基本结论：

问题解决

例1　（1）如图①，AA′，BB′分别是∠EAB，∠DBC的角平分线，若AA′＝BB′＝AB，则∠BAC 的度数为________；

（全国初中数学联赛题）

（2）如图②，四边形ABDC中，△EDC是由△ABC绕顶点C旋转40°所得，顶点A恰好转到AB上一点E的位置，则∠1＋∠2＝________度．

（江苏省竞赛题）

青少年当中的数学爱好者，大多数首先是几何爱好者．

——张景中

斯坦纳-雷米欧司定理

“两条内角平分线相等的三角形是等腰三角形”，这是由德国数学家雷米欧司于1840年提出的，一年多后，瑞士几何学家斯坦纳（1796—1873）首次证明了它，这个问题以“斯坦纳-雷米欧司定理”而闻名于世．

解题思路　对于（1），设∠BAC＝x．把相关的角用含x的式子表示；对于（2），寻找图中全等三角形、等腰三角形．

例2（1）如图①，在等腰Rt△ABC中，AD为斜边上的高，以D为端点任作两条互相垂直的射线与两腰相交于点E，F，连接EF与AD相交于点G，则∠AED与∠AGF的关系为（　）；

A．∠AED＞∠AGF　B．∠AED＝∠AGF

C．∠AED＜∠AGF　D．不能确定

（《学习报》公开赛试题）

（2）如图②，在Rt△ABC中，已知∠C＝90°，∠A＝30°，在直线BC或AC上取一点P，使得△PAB是等腰三角形，则符合条件的P点有（　）．

A．2个　B．4个　C．6个　D．8个

（江苏省竞赛题）

解题思路　对于（1），用含相同的代数式表示∠AED，∠AGF；对于（2），AB既可为等腰△PAB的腰，也可为其底．

例3　如图，△ABC中，AD⊥BC于D，∠B＝2∠C，求证：AB＋BD＝CD．

（天津市竞赛题）

解题思路　如何利用条件∠B＝2∠C？又怎样得到AD＋BD？不同的思考方向，会得到不同的解题方法．

等腰直角三角形是一种特殊的等腰三角形，具有较强的生长性．请看下面问题：

如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为BC中点，DE⊥DF，图中有几个等腰直角三角形？

解等腰三角形相关问题时，常用到以下知识方法：

（1）作等腰三角形顶角平分线；

（2）在未指明边（角）的名称时，应分类讨论．

处理题设条件中的“两倍角”的基本途径是：

（1）向外构造等腰三角形；

（2）对内作角平分线．

例4　如图，在△ABC中，AD是∠BAC的角平分线，M是BC的中点，过M作ME∥AD交BA的延长线于E，交AC于F，求证：BE＝CF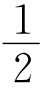＝（AB＋AC）．

（重庆市竞赛题）

解题思路　分两步证明：先证BE＝CF，再证CF＝（AB＋AC）．中点、平行线、平分线给我们丰富的联想：中点→中心对称、中位线，平行线＋平分线→等腰三角形，平分线＋垂线→等腰三角形．

例5　在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．

（1）如图①，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段AM的长；

（2）如图②，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；

（3）如图③，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB＋AN＝

（山东省枣庄市中考题）

解题思路　图③只是图②的一般情形，或构造AB＋AN，，化归、联想可找到问题解决的突破口．

例6　一个三角形可被剖分成两个等腰三角形，原三角形的一个内角为36°，求原三角形最大内角的所有可能值．

（青少年数学国际城市邀请赛试题）

分析与解　剖分的三角形有不同形式，剖分线与36°的角有不同的位置关系，故应全面讨论．

（1）若剖分线不过点B，设剖分线为AD，相应角的度数如图；

（2）若剖分线过点B，设剖分线为BE，相应角的度数如图．

故原三角形的最大内角可能是72°，90°，108°，126°，132°．

解等腰三角形相关问题时，既要关注全等三角形的运用，又应不囿于全等三角形，要善于运用等腰三角形的性质探求新的解题途径．

只有符合下列条件之一的三角形才能被分割成两个等腰三角形：

（1）一个角等于90°；

（2）一个角是另一个角的2倍（x，2x，180°－3x，x≤45°）；

（3）一个角是另一个角的3倍．

如图所示：

例7　如图，△ABC中，∠ABC＝46°，D是BC边上一点，DC＝AB，∠DAB＝21°，试确定∠CAD的度数．

（北京市竞赛题）

解法1　如图①，作△ABD关于AD的轴对称图形△AED，则∠EAD＝21°，AE＝AB，所以，DE＝BD，又∠ADC＝21°＋46°＝67°，故∠ADE＝∠ADB＝180°－67°＝113°，∠CDE＝113°－67°＝46°，连接CE，可证△CDE≌△ABD≌△AED，∠ODE＝∠OED＝46°，得OD＝OE，又DC＝AE，则AO＝CO，∠OCA＝∠OAC，∠COE＝2∠ACO，∠COE＝2×46°＝92°＝2∠ACO．从而∠ACO＝46°＝∠OAC，所以，∠CAD＝∠DAE＋∠EAC＝67°．

图①

解法2　如图②，过A点作AE∥BC，过D点作DE∥AB，连接EC．

∵∠EDC＝∠ABC＝46°，DE＝AB＝CD，

∴∠DCE＝∠CED＝×（180°－46°）＝67°．

∵∠ADC＝∠ABC＋∠BAD＝46°＋21°＝67°．

∴∠ADC＝∠DCE，∴AD＝EC．

∴梯形ADCE为等腰梯形，

∴AC＝DE（等腰梯形对角线相等），

∴AC＝AB＝CD．

∴∠CAD＝∠ADC＝67°．

图②

确定主条件

所谓解题，即从已知条件出发，运用相关知识方法，推出未知结论的过程．当条件众多时，可选择一个条件为主条件，寻找解决问题的突破口．

例8　如图，在△ABC中，已知∠B＝2∠C，AC＝AB＋BD，求证：AD是∠BAC的平分线．

（四川省竞赛题）

解题思路　条件有倍角关系、线段和关系，择其一个为主条件，联想到相应作辅助线的方法，可得到不同解法．

翻折、平移、旋转是作辅助线的重要方法，能使分散的条件集中．

解例7的关键是条件DC＝AB怎样运用，解法1由翻折构造全等三角形，解法2由平移得等腰三角形．

如图，在△ABC中，若∠ABC＝2∠ACB，称△ABC为倍角三角形．作∠DCB＝∠ABC，AD∥BC，则AB＝DC＝AD，这一不变性在解相关问题中有广泛应用．

1．已知△ABC的某两个内角的比是4∶7，且AB＝AC，BD⊥AC于D，BE平分∠ABC交AC于E，则∠EBD 的大小是________．

（“希望杯”邀请赛试题）

2．有一个等腰三角形纸片，若能从一个底角的顶点出发，将其剪成两个等腰三角形纸片，则原等腰三角形纸片的顶角为________．

（江苏省竞赛题）

3．已知等腰△ABC的三边长a，b，c均为整数，且满足a＋bc＋b＋ca＝24，则这样的三角形共有________个．

（四川省竞赛题）

4．（1）已知△ABC是等腰三角形，由顶点A所引BC边的高线恰等于BC边长的一半，则∠BAC＝________；

（北京市竞赛题）

（2）如图钢架中，焊上等长的13根钢条来加固钢架．若AP1＝P1P2＝P2P3＝…＝P13P14＝P14A，则∠A 的度数是________．

（浙江省绍兴市中考题）

［第4（2）题］

（第5题）

（第6题）

5．如图，△ABC内点M满足∠CMB＝100°，线段BM的中垂线交边AB于点P，线段CM的中垂线交边AC于点Q，已知P，M，Q共线，则∠CAB＝________度．

（北京大学自主招生试题）

6．如图，在△ABC中，AB＝BC，在BC上取点M，在MC上取点N，使MN＝NA，若∠BAM＝∠NAC，则∠MAC＝________．

（俄罗斯萨温市竞赛题）

7．已知△ABC中，AB＝6，AC＝8，BC＝11．任作一条直线将△ABC分成两个三角形，若其中有一个三角形是等腰三角形，则这样的直线最多有（　）．

A．3条　B．5条　C．7条　D．8条

8．如图，在△ABC中，AC＝CD，∠CAB－∠B＝30°，则∠BAD为（　）．

A．10°　B．15°　C．20°　D．22．5°

（辽宁省大连市竞赛题）

（第8题）

（第9题）

9．如图，点O在等边△ABC内，∠AOB＝110°，∠BOC＝α，将△BOC绕点C顺时针旋转60°，得到△ADC，连接OD．若△AOD是等腰三角形，则α的不同取值有（　）．

A．1个　B．2个　C．3个　D．无数个

（“希望杯”邀请赛试题）

10．在平面直角坐标系中，已知点A（3，－3），P是y轴上一点，则使△AOP为等腰三角形的点P共有（　）个．

A．2　B．3　C．4　D．5

（海南省竞赛题）

11．如图，在△ABC中，∠BAC，∠BCA的平分线相交于点I，若∠B＝35°，BC＝AI＋AC，则∠BAC的度数为（　）．

A．60°　B．70°

C．80°　D．90°

（第11题）

（“希望杯”邀请赛试题）(www.xing528.com)

12．在△ABC中，∠ABC＝12°，∠ACB＝132°，BM和CN分别是这两个角的外角平分线，且点M，N分别在直线AC和直线AB上，则（　）．

A．BM＞CN　B．BM＝CN

C．BM＜CN　D．BM和CN的大小关系不确定

（全国初中数学联赛题）

13．如图，△ABC是等腰直角三角形，∠BAC＝90°，D是△ABC内一点，且∠DAC＝∠DCA＝15°，求证：BD＝BA．

（湖北省黄冈市竞赛题）

（第13题）

（第14题）

14．如图，在△ABC内，∠BAC＝60°，∠ACB＝40°，P，Q分别在BC，CA上，并且AP，BQ分别为∠BAC，∠ABC的角平分线．求证：BQ＋AQ＝AB＋BP．

（全国初中数学联赛题）

15．如图，在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC，其中∠APB和∠AQC都是直角，点M是BC中点，连接PM，QM，PQ．求证：△PMQ为等腰直角三角形．

（湖北省黄冈市竞赛题）

16．如图，在正五边形ABCDE中，过点C作CD的垂线，与边AB交于点F．求证：AE＋AF＝BE．

（伊朗几何奥林匹克试题）

（第15题）

（第16题）

（第17题）

17．如图，在△ABC中，AB＝AC，∠BAC＝80°，O为△ABC内一点，且∠OBC＝10°，∠OCA＝20°，求∠BAO的度数．

（天津市竞赛题）

18．如图①，在△ABC中，CA＝CB，∠ACB＝α，D为△ABC内一点，将△CAD绕点C按逆时针方向旋转角α得到△CBE，点A，D的对应点分别为点B，E，且A，D，E三点在同一直线上．

（1）填空：∠CDE＝________（用含α的代数式表示）；

（2）如图②，若α＝60°，请补全图形，再过点C作CF⊥AE于点F，然后探究线段CF，AE，BE之间的数量关系，并证明你的结论；

（3）若α＝90°，AC＝，且点G满足∠AGB＝90°，BG＝6，直接写出点C到AG的距离．

（第18题）

（湖北省十堰市中考题）

19．如图①，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重叠部分；……；将余下部分沿∠BnAnC的平分线AnBn＋1折叠，点Bn与点C重合．无论折叠多少次，只要最后一次恰好重合，我们就称∠BAC是△ABC的“好角”．

小丽展示了确定∠BAC是△ABC的好角的两种情形．

情形一：如图②，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合．

情形二：如图③，沿△ABC的∠BAC的平分线AB1折叠，剪掉重叠部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．

（第19题）

探究发现

（1）△ABC中，∠B＝2∠C，经过两次折叠，问∠BAC是不是△ABC的好角？________（填“是”或“不是”）；

（2）小丽经过三次折叠发现了∠BAC是△ABC的好角，请探究∠B与∠C（不妨设∠B＞∠C）之间的等量关系；

根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为________；

（3）小丽找到一个三角形，三个角分别为15°，60°，105°，发现60°和105°的两个角都是此三角形的好角．

请你完成：如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．

（江苏省淮安市中考题）

通过折叠方式定义“△ABC的好角”．对于（3），在（2）的基础上，引入字母表示此三角形另两角．

20．在Rt△ABC中，∠BAC＝90°，边BC上的垂直平分线与AC交于点K，线段BK的垂直平分线与AB交于点L．若CL平分∠ACB，求∠ABC，∠ACB的所有可能值．

（爱尔兰数学竞赛题）

例1　（1）12°　设∠BAC＝x，则∠B′BD＝2x，∠CBD＝4x，∠AA′B＝∠ABA′＝∠CBD＝4x，而∠A′AB＝（180°－x），由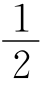（180°－x）＋4x＋4x＝180°，得x＝12°．

（2）110　∠2＝∠OCD＝40°，BC＝DC，∠BCD＝40°，∠1＝＝70°．

例2　（1）B　△DEF为等腰直角三角形，∠AED＝45°＋∠AEG＝∠AGF．

（2）C

例3　延长DB至E，使BE＝AB，连AE，则∠ABC＝2∠E＝2∠C，∠C＝∠E．

例4　如图延长FM至P点，使MP＝MF，连BP，则△BMP≌△CMF，

∴BP＝CF．

∵AD平分∠BAC，AD∥FM，

（例4）

∴∠1＝∠2＝∠3＝∠4＝∠E＝∠P，

∴AE＝AF，BE＝BP＝CF，即AB＋AE＝AB＋AF＝AB＋AC－CF＝CF，

∴CF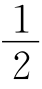＝（AB＋AC）．

例5　（1）AM＝

（2）由△BDE≌△ADF得BE＝AF．

（3）过点M作MP⊥AM，交AB的延长线于点P，证明△PMB≌△AMN，PB＝AN，AP＝AB＋AN＝

例8　下列解法仅供参考，请读者完成．

证法1：如图①，作∠ABC的角平分线交AC于点E，过D作BE的平行线，交AC于点F，交AB的延长线于G．

证法2：如图②，延长DB至E，使BE＝AB，连接AE．

证法3：如图③，延长AB至G，使BG＝BD，连接CG，DG．

（例8）

1．15°或18°　三内角比为4∶7∶7或7∶4∶4．　2．36°或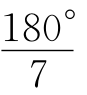

3．3　原式＝（a＋b）（c＋1）＝12×2＝8×3＝6×4，底边的长只能为c，满足条件的三角形有3个：c＝1，a＝b＝6；c＝2，a＝b＝4；c＝3，a＝b＝3．

4．（1）90°或75°或15°

（2）12°　设∠A＝x，则∠A＝∠AP2P1＝∠AP13P14＝x，∠P2P1P3＝∠P13P14P12＝2x，∠P3P2P4＝∠P12P13P3＝3x，…，∠AP7P8＝∠AP8P7＝∠P7P6P8＝7x，由x＋7x＋7x＝180°得x＝12°．

5．20

6．60°　设∠BAM＝∠CAN＝x，∠MAN＝∠AMN＝y，∠ANM＝∠C＋∠CAN，∠BAC＝∠C，即∠ANM＝3x＋y，在△AMN中3x＋3y＝180°，x＋y＝60°，即∠MAC＝60°．

7．C　分别以A，B，C为等腰三角形的顶点的等腰三角形有4个；分别以AB，AC，BC为底的等腰三角形有3个．

8．B

9．C　△COD为等边三角形，当AO＝AD时，由190°－α＝α－60°，得α＝125°；当OA＝OD时，由2（α－60°）＋（190°－α）＝180°，得α＝110°；当OD＝AD时，由2（190°－α）＋（α－60°）＝180°，得α＝140°．

10．C

11．B　在BC上截取CD＝CA，连接ID，则△ACI≌△DCI，AI＝BD＝DI．

12．B　∠ABC＝12°，∠MBC＝（180°－12°）＝84°，∠BCM＝180°－∠ACB＝180°－132°＝48°，∴∠BMC＝180°－84°－48°＝48°，∴BM＝BC．又∠ACN＝（180°－∠ACB）＝（180°－132°）＝24°，∴∠BNC＝180°－∠ABC－∠BCN＝180°－12°－（∠ACB＋∠ACN）＝168°－（132°＋24°）＝12°＝∠ABC，∴CN＝CB，故BM＝BC＝CN．

13．以下证法仅供参考：以AD为边在△ABD内作等边△ADE，先证△EAB≌△DAC，再证△ABE≌△DBE即可．

14．延长AB至M，使BM＝BP，BQ＝QC，证明AC＝AM．

15．延长PM至N，使MN＝PM，则△PBM≌△NCM，连QN，可证△APQ≌△CNQ，得PQ＝QN，△PQN为等腰直角三角形，从而△PMQ为等腰直角三角形．

16．下面证法仅供参考：

如图，延长EA交CF的延长线于点P，通过计算得：∠APF＝∠AFP＝∠BFC＝54°，AF＝AP，AF∥EC，

∴∠ECP＝∠AFP＝∠APF，EC＝EP，

故AE＋AF＝AE＋AP＝EP＝EC＝BE．

17．作∠BAC的角平分线与CO的延长线交于点D，连接BD，则△ABD≌△ACD，则∠ABD＝∠ACD＝30°，∠OBD＝∠ABC－∠OBC－∠ABD＝20°＝∠ABD，∠DOB＝∠OBC＋∠OCB＝40°＝∠DAB，从而△ABD≌△OBD，AB＝OB，即△ABO为等腰三角形，得∠BAO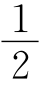＝（180°－40°）＝70°．

（第16题）

18．（1）90°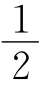－α．

（2）（AE－BE），图略．

（3）点C到AG的距离为1或7，点G、点C在AB同侧或异侧．

19．（1）是　（2）∠B＝n∠C

（3）设另两角分别为4m°，4mn°（m，n为正整数），则4m＋4mn＋4＝180°，得m（n＋1）＝44，经讨论得4m＝4，4mn＝172；4m＝8，4mn＝168；4m＝16，4mn＝160；4m＝44，4mn＝132；4m＝88；4mn＝88．

故该三角形的另外两个角的度数分别为4°，172°；8°，168°；16°，160°；44°，132°；88°，88°．

20．分三种情形考虑：

（1）AC＞AB．

如图①，设∠LBK＝∠LKB＝α．

则∠KLA＝2α，∠LKA＝90°－∠KLA＝90°－2α．

由BK＝KC，得∠KBC＝∠KCB＝∠BKA＝［（90°－α）＋2α］＝45°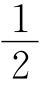＋α．

作LT⊥BC，垂足为T．

因为CL平分∠ACB，所以LT＝LA．

又LB＝LK，∠BTL＝∠KAL＝90°

（第20题）

∴△BTL≌△KAL，得∠LBT＝∠LKA，α＋＝90°－2α，∴α＝18°，得∠ABC＝45°＋α＝54°，

∴∠ACB＝90°－∠ABC＝36°．

（2）AC＜AB．

如图②，设∠LBK＝∠LKB＝α．

则∠KLA＝2α，∠LKA＝90°－∠KLA＝90°－2α．

作LT⊥BC，垂足为T．

因为CL平分∠ACB，所以LT＝LA．

由LB＝LK，∠BTL＝∠KAL＝90°，

∴△BTL≌△KAL，得∠LBT＝∠LKA＝90°－2α，∠CKB＝∠CBK＝90°－α，∴CB＝CK．

又BK＝CK，则△BKC为等边三角形．

故∠CBK＝90°－α＝60°⇒α＝30°，

∴∠ABC＝90°－2α＝30°，∠ACB＝∠KCB＝60°．

（3）AC＝AB，此种情况不成立．

（第20题）