全等三角形与莫比乌斯带的奇异曲线

莫比乌斯（1790—1868），德国数学家、天文学家．1858年，莫比乌斯在法国巴黎科学协会举办的数学论文比赛上，公布了他发现的奇异的曲线：这个曲面尽管每一小段都有正反两面，但从整体上看却只有一个面，即从曲面一点出发不经过边界，可以走到这一点的反面，这就是“莫比乌斯带”，被视为数学珍品．

知能概述

全等三角形是研究三角形、四边形的主要工具，是解决有关线段、角等问题的一个出发点，线段相等、线段的和差倍分关系、角的关系、两直线位置关系等的证明问题常转化为证明三角形全等．

熟悉以下基本图形、基本结论：

问题解决

例1　如图，在四边形ABCD中，AC平分∠BAD，过C作CE⊥AB于E，并且AE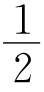＝（AB＋AD），那么，∠ABC＋∠ADC 的度数是________．

（上海市竞赛题）

数学是一种精神，一种理性的精神．正是这种精神，激发、促进、鼓舞并驱使人类的思维得以运用到最完善的程度．

——克莱因

分　地

苏轼任凤翔签书判官时，有兄弟四人曾为分遗产到大堂告状．

如图，兄弟四人继承先父土地一块，父亲临终前曾叮嘱：四人所得不仅数量无差别，而且还要形状与原地块相同，请问该如何分地？

解题思路　运用角平分线翻折构造全等三角形．

例2　在△ABC中，AC＝5，中线AD＝4，则边AB的取值范围是（　）．

A．1＜AB＜9　B．3＜AB＜13

C．5＜AB＜13　D．9＜AB＜13

（陕西省竞赛题）

解题思路　线段AC，AD，AB不是同一个三角形的三条边，通过中线倍长，将分散的条件加以集中．

例3　如图，已知四边形ABCD中，∠ACB＝∠BAD＝105°，∠ABC＝∠ADC＝45°，求证：CD＝AB．

（天津市竞赛题）

解题思路　AB，CD所在的三角形不全等，通过作辅助线构造全等三角形是证明的关键，即以一个三角形为基准，构造一个与之全等的三角形．

如图①，以△ABC为基准，在△ACD中以CD为大边构造一个与△ABC全等的三角形；

如图②，以△ACD为基准，在△ABC上补出一个与△ACD全等的三角形；

如图③，由45°联想到等腰直角三角形等．

构造的过程是想象的过程，也是逻辑思考的过程，你有其他的构造方法吗？

有些问题的条件与结论之间的联系不明显，有时需要添加恰当的辅助线构造全等三角形．现阶段，利用中线（倍长）、角平分线（翻折）、垂线或平行线是构造全等三角形的基本方法．

变式练习是中国数学教育的一大特色．

“变式”即有目的、有计划地对命题进行合理的转化，通过转换问题的内容和形式、转换命题的非本质特征、变换问题中的条件或结论等方式，使问题的非本质特征时隐时现而本质特征保持不变．

例4　如图，已知AC∥BD，EA，EB分别平分∠CAB，∠DBA，CD过点E．

求证：AB＝AC＋BD．

（“希望杯”邀请赛试题）

解题思路　截长法（或补短法）是证明线段和差问题的基本方法．即在AB上截取AF，使AF＝AC，以下只要证明FB＝BD．

例5　如图①，在平面直角坐标系中，已知A（－4，0），B（0，4），C（0，2），D（2，0）．

（1）求证：AC＝BD；

（2）如图②，设E，F分别是AC，BD的中点，试判断△OEF的形状，并说明理由；

（3）如图③，延长AC交BD于点P，连接OP，试求的值．

解题思路　对于（3），∠PAB＋∠PBA＝∠APD，即求的值，猜测OP平分∠APD，怎样证明？

例6　下列四个判断：

（1）有两边及其中一边上的高对应相等的两个三角形全等；

（2）有两边及第三边上的高对应相等的两个三角形全等；

（3）三角形6个边、角元素中，有5个元素分别相等的两个三角形全等；

（4）一边及其他两边上的高对应相等的两个三角形全等．

上述判断是否正确？若正确，说明理由；若不正确，请举出反例．

（江苏省竞赛题）

边、角、中线、角平分线、高是三角形的基本元素，从以上诸元素中选取三个条件进行有机组合可判定两个三角形全等的命题，但这些命题有真有假．

解　判断（1）、（2）、（3）、（4）都不正确．

判断（1）的反例：

如图①，在△ABC中，AC＝AC，BC＝B′C，高AH＝AH，但这两个三角形不全等．

判断（2）的反例：

如图②，在△ABC、△ABC′中，AB＝AB，AC＝AC′，高AH＝AH，但两个三角形不全等．

判断（3）的反例：

设△ABC的三边长分别为AB＝16，AC＝24，BC＝36；△A′B′C′的三边长分别为A′B′＝24，A′C′＝36，B′C′＝54．由于△ABC与△A′B′C′的对应边成比例，故△ABC∽△A′B′C′，从而它们有5个边、角元素分别相等：∠A＝∠A′，∠B＝∠B′，∠C＝∠C′，AC＝A′B′，BC＝A′C′，但它们不全等．

判断（4）的反例：

如图③，在△ABC中，AD，BE分别是边BC，AC上的高，作∠BAF＝∠BAC，延长BC，FA交于点C′，则高BF＝BE，AD＝AD，又AB＝AB，但△ABC与△ABC′不全等．

综上所述，题中四个判断都不正确．

半角模型

半角模型是指有公共顶点，锐角等于较大角的一半，且组成这个较大角的两边相等，通过翻折或旋转，将角的倍分关系转化为角的相等关系，并进一步构造全等或相似三角形，弱化条件，变更载体，从而构建模型，把握问题的本质．

例7　（1）问题背景：如图①，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系．小王同学探究此问题的方法是，延长FD到点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论．他的结论应是________；

（2）探索延伸：如图②，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是BC，CD上的点，∠EAF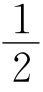＝∠BAD，上述结论是否仍然成立，并说明理由；

例6中的第（3）个判断是著名数学家、教育家波利亚曾提出的一个饶有趣味的初等几何问题．

数学是关于模式的学科，笛卡儿曾说：“我所解决的每一个问题都将成为一个范例，用于解决其他问题．”

例7创设了一个特殊位置下的问题情境，通过条件的改变，探讨对结论的影响．解决问题的层层推进，让我们感悟到数学结论的形成过程，揭示了问题的本质．

（3）实际应用：如图③，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里／小时的速度前进，舰艇乙沿北偏东50°的方向以80海里／小时的速度前进，1．5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．

（山东省德州市中考题）

解题思路　对于实际应用，通过作辅助线完善图形，为半角模型的应用创造条件．

1．如图，AB＝2，BC＝AE＝6，CE＝CF＝7，BF＝8，则四边形ABDE与△CDF 面积的比值是________．

（第1题）

（北京市竞赛题）

2．已知，如图，△ABC≌△A′B′C′，AD，A′D′分别是△ABC和△A′B′C′的高．求证：AD＝A′D′．

（第2题）

可以反过来思考，提出一些问题：已知△ABC和△A′B′C′中，高AD等于高A′D′，再增加以下各组条件：

①∠B＝∠B′，∠C＝∠C′；

②∠B＝∠B′，AB＝A′B′；

③BC＝B′C′，AB＝A′B′；

写出能分别判定△ABC≌△A′B′C′的所有条件组的序号：________．

（《时代学习报》数学文化节试题）

3．如图，将△ABC绕着C点按顺时针方向旋转20°，B点落在B′点位置，A点落在A′点位置，若AC⊥A′B′，则∠BAC＝________．

（江苏省竞赛题）

（第3题）

（第4题）

4．如图，点C在线段AB上，DA⊥AB，EB⊥AB，FC⊥AB，且DA＝BC，EB＝AC，FC＝AB，∠AFB＝51°，则∠DFE＝________．

（北京市竞赛题）

在“变”的表象中寻找“不变”的本质，从“不变”的本质中探寻“变”的规律．

5．如图，△ABC中，BD平分∠ABC，AD⊥BD于点D，S△BCD＝45，S△ADC＝20，则S△ABD ＝________．

（第5题）

（“华罗庚金杯”少年数学邀请赛试题）

6．一个三角形的三条边的长分别为3，5，7，另一个三角形的三条边的长分别为3，3x－2，2x－1，若这两个三角形全等，则x的值是________．

（“希望杯”邀请赛试题）

7．在△ABC中，高AD，BE所在的直线相交于点G，若BG＝AC，则∠ABC的度数为（　）．

A．45°　B．135°　C．60°或120°　D．45°或135°

（湖北省黄冈市竞赛题）

8．如图，在△ABC中，AC＝BC，∠ACB＝90°，AD平分∠BAC，BE⊥AD交AC的延长线于F，E为垂足．则结论：①AD＝BF；②CF＝CD；③AC＋CD＝AB；④BE＝CF；⑤BF＝2BE．其中正确结论的个数是（　）．

A．1　B．2　C．3　D．4

（河北省竞赛题）

（第8题）

（第9题）

（第10题）

9．如图，在四边形ABCD中，对角线AC平分∠BAD，AB＞AD，下列结论中正确的是（　）．

A．AB－AD＞CB－CD

B．AB－AD＝CB－CD

C．AB－AD＜CB－CD

D．AB－AD与CB－CD的大小关系不确定

（江苏省竞赛题）

10．如图，△ABC是一个等腰直角三角形，四边形DEFG是其内接正方形，H是正方形的对角线的交点．那么，由图中的线段所构成的三角形中相互全等的三角形的对数为（　）．

A．12　B．13　C．26　D．36

（江西省竞赛题）

11．下面三个判断：

（1）存在这样的三角形，它有两条角平分线互相垂直；

（2）存在这样的三角形，它的三条高的比是1∶2∶3；

（3）存在这样的三角形，其中一边上的中线不小于其他两边和的一半．

其中，正确的判断有（　）．

A．0个　B．1个　C．2个　D．3个

（江苏省竞赛题）

12．如图，△ABC中，∠A＝90°，角平分线BD，CE交于点I，IF⊥CE交CA于F，IH⊥AB于H．下列结论：①∠DIF＝45°；②CF＋BE＝BC；③AE＋AF＝2AH；④S四边形BEDC＝2S△IBC．则正确结论的个数为（　）．

（第12题）

A．1个　B．2个　C．3个　D．4个

13．（1）阅读理解：

如图①，在△ABC中，若AB＝10，AC＝6，求BC边上的中线AD的取值范围．

解决此问题可以用如下方法：延长AD到点E使DE＝AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD）．把AB，AC，2AD集中在△ABE中，利用三角形三边的关系即可判断．

中线AD 的取值范围是________．

（2）问题解决：(www.xing528.com)

如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF．求证：BE＋CF＞EF；

（3）问题拓展：

如图③，在四边形ABCD中，∠B＋∠D＝180°，CB＝CD，∠BCD＝140°，以C为顶点作一个70°角，角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．

（第13题）

（贵州省贵阳市中考题）

14．如图，在△ABC中，∠ABC＝60°，AD，CE分别平分∠BAC，∠ACB．求证：AC＝AE＋CD．

（湖北省武汉市竞赛题）

（第14题）

（第15题）

15．如图，已知AB＝CD＝AE＝BC＋DE＝2，∠ABC＝∠AED＝90°，求五边形ABCDE的面积．

（广西壮族自治区竞赛题）

16．如图，在△DEF中，∠EDF＝15°，DP是∠EDF的平分线，DP⊥DQ，且FQ＝ED＋DF，求∠Q，∠E的度数．

（第16题）

（第17题）

（“希望杯”邀请赛试题）

17．如图，在六边形ABCDEF中，AB＝BC＝CD＝DE＝EF＝FA，且∠A＋∠C＋∠E＝∠B＋∠D＋∠F．

求证：∠A＝∠D，∠B＝∠E，∠C＝∠F．

（北京市竞赛题）

18．问题提出：学习了三角形全等的判定方法（即“SAS”“ASA”“AAS”“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

初步思考：我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E．然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

深入探究：第一种情况：当∠B是直角时，△ABC≌△DEF．

（1）如图①，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E＝90°，根据________，可以知道Rt△ABC≌Rt△DEF．

第二种情况：当∠B是钝角时，△ABC≌△DEF．

（第18题）

（2）如图②，在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是钝角．求证：△ABC≌△DEF．

第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．

（3）在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）

（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接填写结论：

在△ABC和△DEF中，AC＝DF，BC＝EF，∠B＝∠E，且∠B，∠E都是锐角，若________，则△ABC≌△DEF．

（第18题）

（江苏省南京市中考题）

19．如图，已知凸四边形ABCD满足∠ADC＝135°，∠ADB－∠ABD＝2∠DAB＝4∠CBD，若BC＝，求证：AB＝BC＋AD．

（第19题）

（伊朗几何奥林匹克试题）

20．（1）设梯形两底边长为整数，求证：它可以分割为若干个彼此全等的三角形．

（环球城市数学奥林匹克试题）

（2）①证明：2018可表示为两个正整数的平方和；

②证明：存在这样的三角形，可把它分割为2018个全等的三角形．

（北京市竞赛题）

例1　180°　在AB上截取AF＝AD，连CF，则△ADC≌△AFC，∠ADC＝∠AFC，可证明BE＝EF，△CEF≌△CEB，∠ABC＝∠CFE，故∠ABC＋∠ADC＝∠CFE＋∠AFC＝180°．

例2　B　延长AD到E，使DE＝AD，连接EC，则△ABD≌△ECD，AB＝EC，2AD－AC＜AB＜2AD＋AC．

例3　略

例4　如图，在AB上截取AF，使AF＝AC，连接EF．

由△ACE≌△AFE，得∠C＝∠AFE，

∵AC∥BD，　∴∠C＋∠D＝180°．

而∠5＋∠AFE＝180°，则∠5＝∠D．

在△BEF和△BED中，∵∠5＝∠D，∠3＝∠4，BE＝BE，

∴△BEF≌△BED，得BF＝BD．　∴AB＝AF＋BF＝AC＋BD．

例5　（1）证明△ACO≌△BDO，得AC＝BD．

（2）证明△AEO≌△BFO，∠EOF＝90°，可得△OEF为等腰直角三角形．

（3）作OM⊥AP于点M，ON⊥BD于点N，可证明OM＝ON，则OP平分∠APD，故

（例4）

例7　（1）问题背景：　EF＝BE＋DF

（2）探索延伸：　EF＝BE＋DF仍然成立，延长FD至点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF即可．

（3）实际应用：　如图，连接EF，延长AE，BF相交于点C，在四边形AOBC中，∵∠AOB＝30°＋90°＋20°＝140°，∠EOF＝70°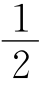＝∠AOB，又∵OA＝OB，

∠OAC＋∠OBC＝180°，符合“探索延伸”中的条件，

∴EF＝AE＋BF＝1．5×（60＋80）＝210（海里）．

（例7）

1．1　△AEC≌△BCF．

2．①

③的反例如下图

（第2③题）

3．70°

4．39°　连接BD，△ABD≌△CFB，△ABE≌△FCA，得DB＝FB，AE＝AF，则△DBF，△EAF都是等腰直角三角形，∠EFB＝6°，∠DFA＝6°，∠DFE＝∠AFB－∠EFB－∠DFA＝39°．

5．25　延长AD交BC于点E，则AD＝DE，S△ADC＝S△CDE，S△ABD＝S△BDE．

6．3　7．D

8．D　①②③⑤正确．

9．A　10．C　11．A

12．D　对于④，证明S△EID＋S△BEI＋S△CDI＝S△BIC．

13．（1）2＜AD＜8

（2）略

（3）延长AB至点N，使BN＝DF，证明△NBC≌△FDC，△NCE≌△FCE，由此可得BE＋DF＝EF．

14．在AC上截取AF＝AE，连接OF，∠AOC＝90°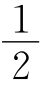＋∠B＝120°，得∠DOC＝∠AOE＝∠AOF＝60°，则∠FOC＝60°，可证明△FOC≌△DOC，得DC＝FC，故AC＝AF＋FC＝AE＋DC．

15．延长DE至点F，使EF＝BC，连AC，AD，AF，可证明△ABC≌△AEF，△ACD≌△AFD，故S五边形ABCDE＝2S△ADF＝4．

16．延长FD至点G，使DG＝ED，连接GQ，则△EDQ≌△GDQ，∠E＝∠G＝∠FQG＝2∠DQE，∠EDQ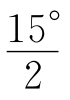＝＋90°＝97．5°，因∠EDQ＋∠E＋∠DQE＝180°，故∠EQD＝27．5°，∠E＝55°．

（第16题）

17．如图，连接AE，EC，CA．

因为六边形内角和为720°，又∠A＋∠C＋∠E＝∠B＋∠D＋∠E，

所以，∠BAF＋∠BCD＋∠DEF＝∠ABC＋∠CDE＋∠EFA＝360°．

如图，作△EFP≌△CBA，连接AP，则

∠AFP＝360°－∠EFA－∠PFE＝360°－∠EFA－∠ABC＝∠CDE＝∠D．

于是，△AFP≌△CDE⇒AP＝CE．

故△ACE≌△EPA⇒∠CAE＝∠PEA．

又∠BAC＝∠BCA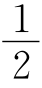＝（180°－∠B），∠FAE＝∠FEA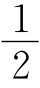＝（180°－∠F），

（第17题）

故∠BAC＋∠FAE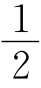＝（180°－∠B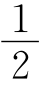）＋（180°－∠F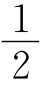）＝（360°－∠B－∠F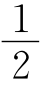）＝∠D．

又∠CAE＝∠PEA＝∠PEF＋∠AEF＝∠BAC＋∠FAE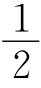＝∠D，

则∠BAF＝（∠BAC＋∠FAE）＋∠CAE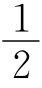＝∠D＋∠D＝∠D，即∠A＝∠D．

同理，∠B＝∠E，∠C＝∠F．

18．（1）HL

（2）如图①，分别过点C，F作对边AB，DE上的高CG，FH，其中G，H为垂足．

先证明△BCG≌△EFH，得CG＝FH；再证明△ABC≌△DEF．

（第18题）

（3）如图②，△DEF就是所求作的三角形．

（4）本题答案不唯一，此答案供参考：∠B≥∠A．

19．由已知条件，可设∠CBD＝α．

则∠DAB＝2α，∠ADB－∠ABD＝4α．

又在△ABD中，有

∠ADB＋∠ABD＝180°－∠A＝180°－2α，

∴∠ADB＝90°＋α，∠ABD＝90°－3α，

∴∠DAB＋∠CBA＝2α＋［（90°－3α）＋α］＝90°．

设AD，BC的延长线交于点P．

由∠DAB＋∠CBA＝90°，得∠APB＝90°．

又∠PDC＝180°－∠ADC＝45°，于是，△PCD为等腰直角三角形．

结合已知条件，知

（第19题）

延长AP到点Q，使得PQ＝PD，则DQ＝2DP＝BC

∴△DPB≌△QPB，得∠CBD＝∠CBQ＝α，∠ABQ＝α＋α＋（90°－3α）＝90°－α．

又∠A＝2α，因此，△ABQ为等腰三角形，AB＝AQ．

故AB＝AQ＝DQ＋AD＝BC＋AD．

20．（1）设两底边长为n，m，且n≤m．当m＝n或n＋1时两底的对应等分点AiBi，AiBi＋1相连，由于平行四边形被一条对角线分成的两个三角形全等，故得到全等的三角形分割．

［第20（1）题］

当m≥n＋2时将两腰（m－n）等分，过分点作底边的平行线将原梯形分割为（m－n）个梯形．每个按上述（n，n＋1）方式分割为全等的三角形．由于任意两层的同方向平行四边形彼此全等，故各层的所有三角形彼此全等．

（2）①若存在正整数x，y，使得2018＝x2＋y2，由于2018被4除余2，则x，y必同为奇数．

又奇数的平方的个位数必为1，5，9之一，故x2，y2的个位均为9，即x，y的个位数为3或7．

设x≤y，则1009≤y2＜2018．

于是，y的可能值只有33，37，43．

经计算得2018＝132＋432．　（＊）

②由（＊）构想：将直角边长为13，43的一个直角三角形引斜边上的高线，分该三角形为两个相似的直角三角形，其斜边分别为13，43，将斜边为13的直角三角形各边13等分，分成169个斜边为1的小直角三角形；将斜边为43的直角三角形各边43等分，分成1849个斜边为1的小直角三角形．合计共分割成了169＋1849＝2018个斜边为1的彼此全等的直角三角形．

因此，满足题设要求的三角形是存在的．