一次函数揭示事物数量关系和运动规律

函数图象直观形象地描绘了事物间的数量关系、运动规律．

数学的和谐不仅在于它能解释自然，仿效自然，还在于它能描述自然．

左上图是笛卡儿得到的富有诗意和数学美感的“茉莉花瓣”——笛卡儿曲线，它是函数x3＋y3＝3axy的图象；左下图是心脏线，是函数（x2＋y2＋ax）2＝a2（x2＋y2）的图象，是荷兰数学家考尔斯玛发现的．

知能概述

函数，是人类的一种重要思维方式．

函数，是一种数学概念，是一个数学模型，是再现客观事物变化过程的数学工具，是一种对应关系．

形如y＝kx＋b（k≠0）的函数叫作一次函数，它的图象是一条直线，与坐标轴的交点分别是的符号决定图象的大致位置及单调性．

一次函数与一次方程、不等式有深刻的内在联系，一次方程和不等式分别着眼于数量之间的相等或不等关系，而一次函数则从研究数量的变化规律入手将两者统一起来，并实现在一定条件下的相互转化．

解含参数的动直线问题，善于发现定点、定直线，是探寻最值的关键．

问题解决

例1　（1）已知某一次函数当自变量取值范围是2≤x≤6时，函数值的取值范围是5≤y≤9，那么，此一次函数解析式为________．

（广西壮族自治区竞赛题）

（2）设直线（n为自然数）与两坐标轴围成的三角形面积为Sn（n＝1，2，…，2000），则S1＋S2＋…＋S2000的值为________．

（河北省竞赛题）

在现代实验科学中，能否接受数学方法或与数学相近的物理学方法，已愈来愈成为该学科成功与否的主要标准．

——冯·诺依曼

定性思考

求证：无论k取何值，关于x的一次函数（2k－1）x＋（k＋3）y－（k－11）＝0的图象必须经过定点．

（“希望杯”邀请赛试题）

解题思路　对于（1），因y随x的变化情况不确定，故应分类讨论；对于（2），求出直线与x轴、y轴的交点坐标，从一般形式入手，把Sn用含n的代数式表示．

例2　（1）设b＞a，将一次函数y＝bx＋a与y＝ax＋b的图象画在平面直角坐标系内，则有一组a，b的取值，使得下面四个图中的一个为正确的是（　）．

（全国初中数学联赛题）

（2）一个一次函数的图象与直线平行，与x轴、y轴的交点分别为A，B，并且过点（－1，－25），则在线段AB上（包括端点A，B），横、纵坐标都是整数的点有（　）．

A．4个　B．5个　C．6个　D．7个

（全国初中数学联赛题）

解题思路　对于（1），由形到数判定a，b的符号；对于（2），求出过A，B两点直线的解析式，将问题转化为求不定方程的整数解．

例3　如图，直线y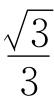＝－x＋1与x轴、y轴分别交于点A，B，以线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC＝90°，如果在第二象限内有一点，且△ABP的面积与△ABC的面积相等，求a的值．

（天津市竞赛题）

由图象获取信息，解决相关问题，培养数形结合能力，发展形象思维，是函数学习的重要方面，具体包括：

（1）看图找点；

（2）见形想式；

（3）建模求解．

上升线表示因变量随自变量取值的增加而增加；下降线表示因变量随自变量取值的增加而减少；水平线表示因变量随自变量取值的增加而未发生改变．

解题思路　由S△ABP＝S△ABC建立含a的方程，解题的关键是把S△ABP表示为有边落在坐标轴上的三角形面积的和差．

例4　已知直线

（1）说明无论k取不等于1的任何实数，此直线都经过某一定点，并求出此定点的坐标；

（2）若点B（5，0），点P在y轴上，点A为（1）中确定的定点，要使△PAB为等腰三角形，求直线PA的解析式．

（浙江省湖州市竞赛题）

解题思路　对于（1），对k赋值或整理成关于k的方程；对于（2），设P（0，m），由勾股定理建立关于m的方程，但需讨论．

例5　求在直角坐标平面中不等式｜x｜＋｜y｜≤3围成的面积．

（香港特别行政区中学数学竞赛题）

分析与解　在理解平面内y≥kx＋b或y≤kx＋b意义的基础上，去掉绝对值符号，把不等式问题转化为一次函数问题加以解决．

由绝对值的意义，不等式｜x｜＋｜y｜≤3所围多边形，即4条直线x＋y＝3，x－y＝3，－x＋y＝3，－x－y＝3所围的多边形（图中阴影部分），其面积为

例6　在直角坐标系xOy中，一次函数y＝kx＋b（k≠0）的图象与x轴、y轴的正半轴分别交于点A，B，且使得△AOB的面积值等于｜OA｜＋｜OB｜＋3．

（1）用b表示k；

（2）求△OAB面积的最小值．

（浙江省竞赛题）

解一次函数与直线形的综合问题时，常用到勾股定理、全等三角形、相似三角形等知识，善于促成线段与坐标的转换是解这类问题的关键．

如图y≤kx＋b表示直线y＝kx＋b以及它下方的部分；同理，y≥kx＋b表示直线y＝kx＋b以及它上方的部分．

例6通过配方，求得相应代数式的最值．

转换视角

视角不同，方法殊异．转换视角，多视角看问题，能提高我们解决问题的灵活性、深刻性．

居高临下，用函数的视角、方法分析问题，由问题的条件构造函数关系式，使原问题在函数关系中实现转化．

例7　（1）对于给定实数a，记M（a）是三数a，6－a，2a＋4中最小的数，则在数M（－2018），M（－2017），M（－2016），…，M（－1），M（0），M（1），…，M（2016），M（2017），M（2018）中最大的数是________．

（2）方程组共有（　）组解．

A．1　B．2　C．3　D．4　E．5

（美国数学竞赛题）

分析与解　构造一次函数，借助图象解决问题，形象而直观．

（1）如图①，在同一坐标系中画出三个一次函数y＝x，y＝6－x，y＝2x＋4的图象，发现M（3）最小，最小值为3．

（2）如图②，作函数x＋3y＝3，｜｜x｜－｜y｜｜＝1的图象，而函数有三个交点

1．（1）不论k为何值，解析式（2k－1）x－（k＋3）y－（k－11）＝0表示的函数图象经过一定点，则这个定点是________．

（2）在平面直角坐标中，坐标原点O到一次函数y＝kx－2k＋1的图象的距离的最大值为________．

2．在平面直角坐标系内有两点P（－1，1），Q（2，2），一次函数y＝kx－1的图象与线段PQ的延长线相交（交点不包括Q），则实数k的取值范围是________．

（“新知杯”竞赛题）

3．在直角坐标系中，x轴上的动点M（x，0）到定点P（5，5），Q（2，1）的距离分别为MP和MQ，那么，当MP＋MQ取最小值时，点M的坐标为______．

（全国初中数学联赛题）

4．（1）直线y＝3x＋k＋2与直线y＝－x＋2k的交点在第二象限，且k是正整数，则k的值是________，交点的坐标是________．

（“希望杯”邀请赛试题）

函数不是一种数，而是描述变化规律的一种数学模型．函数的功能就是人类的思维，“函数般的表达思想”的本质是：发现事物之间的关系．

（2）设直线l1：y＝kx＋k－1和直线l2：y＝（k＋1）x＋k（k为正整数）及x轴围成的三角形面积为Sk，则S1＋S2＋…＋S2006＝________．

（浙江省竞赛题）

5．若四条直线x＝1，y＝－1，y＝3，y＝kx－3所围成的凸四边形的面积等于12，则k的值为________．

（天津市竞赛题）

6．已知在平面直角坐标系中有如下36条直线：

y＝18x＋17，y＝17x＋16，…，y＝2x＋1，y＝x，

y＝－x，y＝－2x＋1，…，y＝－17x＋16，y＝－18x＋17，

那么由这些直线相交所构成的交点有________个．

（“华罗庚金杯”少年数学邀请赛试题）

7．已知点A（－4，0），B（2，0）．若点C在一次函数y＝x＋2的图象上，且△ABC是直角三角形，则点C的个数是（　）．

A．1　B．2　C．3　D．4(www.xing528.com)

（“希望杯”邀请赛试题）

8．已知abc≠0，且，则直线y＝px＋p一定通过（　）．

A．第一、二象限　B．第二、三象限

C．第三、四象限　D．第一、四象限

（全国初中数学联赛题）

9．已知点A，B分别在一次函数y＝x，y＝8x的图象上，其横坐标分别为a，b（a＞0，b＞0）．若直线AB为一次函数y＝kx＋m的图象，则当是整数时，满足条件的整数k的值共有（　）个．

A．1　B．2　C．3　D．4

（江苏省竞赛题）

10．如图，平面直角坐标系xOy中，点A的坐标为（9，6），AB⊥y轴，垂足为B，点P从原点O出发向x轴正方向运动，同时，点Q从点A出发向点B运动，当点Q到达点B时，点P，Q同时停止运动，若点P与Q的速度之比为1∶2，则下列说法正确的是（　）．

（第10题）

A．线段PQ始终经过点（2，3）

B．线段PQ始终经过点（3，2）

C．线段PQ始终经过点（2，2）

D．线段PQ不可能始终经过某一定点

（江苏省泰州市中考题）

11．若一次函数y＝x＋5的图象经过点P（a，b）和Q（c，d），则ad＋bc－acbd的值是（　）．

A．9　B．16　C．25　D．－25

（“希望杯”邀请赛试题）

12．一条经过坐标原点的直线，与直线围成一个等边三角形，则这个等边三角形的周长为（　）．

（美国数学竞赛题）

13．如图，在平面直角坐标系中，以A（2，0），B（0，t）为顶点作等腰直角△ABC，其中∠ABC＝90°，点C在AB上方，求OC的最小值．

（第13题）

（第14题）

14．如图，直线OB是一次函数y＝2x的图象，点A的坐标为（0，2），在直线OB上找点C，使得△ACO为等腰三角形，求点C的坐标．

（江苏省竞赛题）

15．探究活动一：

如图①，某数学兴趣小组在研究直线上点的坐标规律时，在直线AB上的三点A（1，3），B（2，5），C（4，9），有，发现kAB＝kAC．兴趣小组提出猜想：若直线y＝kx＋b（k≠0）上任意两点坐标P（x1，y1），Q（x2，y2）（x1≠x2），则是定值．通过多次验证和查阅资料得知，猜想成立，kPQ是定值，并且是直线y＝kx＋b（k≠0）中的k，叫作这条直线的斜率．

请你应用以上规律直接写出过S（－2，－2），T（4，2）两点的直线ST的斜率kST ＝________．

探究活动二：

数学兴趣小组继续深入研究直线的“斜率”问题，得到正确结论：任意两条不和坐标轴平行的直线互相垂直时，这两条直线的斜率之积是定值．

如图②，直线DE与直线DF垂直于点D，D（2，2），E（1，4），F（4，3）．请求出直线DE与直线DF的斜率之积．

综合应用：

如图③，⊙M为以点M为圆心，MN的长为半径的圆，M（1，2），N（4，5），请结合探究活动二的结论，求出过点N的⊙M的切线的解析式．

（第15题）

（山东省日照市中考题）

16．如图，已知一次函数y＝kx＋b的图象过点P（1，4），且分别与x轴、y轴交于点A，B，当△AOB的面积最小时，求k，b的值．

（第16题）

（山东省竞赛题）

17．已知函数y＝｜x＋1｜－2｜x－1｜＋｜x＋2｜．

（1）在直角坐标系中作出函数图象；

（2）已知关于x的方程kx＋3＝｜x＋1｜－2｜x－1｜＋｜x＋2｜（k≠0）有三个解，求k的取值范围．

（“创新杯”竞赛题）

18．是否存在两两不同的实数a，b，c，使得平面直角坐标系中三条直线y＝ax＋b，y＝bx＋c，y＝cx＋a共点？

（北京大学自主招生试题）

19．平面直角坐标系中，正方形ABCD四个顶点的坐标分别为（－1，－1），（1，－1），（1，1），（－1，1）．设正方形ABCD在y＝｜x－a｜＋a的图象以上部分的面积为S，试求S关于a的函数关系式，并写出S的最大值．

（“希望杯”邀请赛试题）

20．（1）在平面直角坐标系中，求由不等式组确定的区域面积．

（上海市竞赛题）

（2）在平面直角坐标系中，求由折线｜x－1｜＋｜x＋1｜＋｜y｜＝3围成的图形的面积．

（全国高中数学联赛题）

例1　（1）y＝x＋3或y＝－x＋11　设所求的一次函数解析式为y＝kx＋b，

①若k＞0时，当x＝2时，y＝5，当x＝6时，y＝9，求得y＝x＋3；

②若k＜0时，当x＝2时，y＝9，当x＝6时，y＝5，求得y＝－x＋11．

6．326　这36条直线可分为两类，一类是过（－1，－1）点且与x轴正方向成锐角的18条直线，另一类是与之关于y轴对称的过（1，－1）点且与x轴正方向成钝角的另18条直线，每一类直线与另一类的每条直线都有一个交点，且这些交点均不相同，共18×18＝324（个），另外还有（1，－1）与（－1，－1）这两点，所以总共有326个交点．

7．B　点A在直线y＝x＋2上．

8．B　p＝2或p＝－1．

9．B　A（a，a），B（b，8b），代入y＝kx＋m，得或8．

（2）设y＝kx＋3，则y＝｜x＋1｜－2｜x－1｜＋｜x＋2｜（k≠0）．

因此，所给方程有三个解，实际上就是这两个函数的图象有三个交点．如图，令点A（1，5），点B（0，3），则y＝kx＋3的图象是过定点B的直线．当y＝kx＋3过点A时，此直线之斜率k＝2，显然，这两个函数的图象只有两个交点．故当0＜k＜2时，这两个函数的图象有三个交点．

18．假设存在两两不同的实数a，b，c，使得平面直角坐标系中三条直线y＝ax＋b，y＝bx＋c，y＝cx＋a共点，联立y＝ax＋b，y＝bx＋c，解得联立y＝bx＋c，y＝cx＋a，解得＝（cb）2＝（c－a＋a－b）2⇒（c－a）2＋（c－a）（a－b）＋（a－b）2＝0．

（第17题）

∵x2＋x＋1＝0无实根，

∴（＊）式不成立，即不存在两两不同的实数a，b，c，使得平面直角坐标系中三条直线y＝ax＋b，y＝bx＋c，y＝cx＋a共点．

19．（1）当a≥1时，y＝｜x－a｜＋a的图象与正方形无公共部分，如图①所示S＝0．

（第19题）

（2）当0≤a＜1时，如图②所示．S＝（1－a）×2（1－a）＝（1－a）2．

（3）当－1≤a＜0时，如图③所示．S＝

（4）当a＜－1时，如图④所示．S＝2．

所以，S的最大值为2．

20．（1）显然，区域既关于x轴对称，又关于y轴对称．因此，可先假定x≥0，y≥0．

由画出区域在第一象限（包括坐标轴）的部分，再对称作出整个区域，如图①．

图①

所求区域的面积是边长为4的正方形面积减去八个腰长为1的等腰直角三角形面积，即42－8×＝12．

（2）当y≥0时，

其图象为图②中折线ABCD．

当y≤0时，只需将上述折线沿x轴翻折．

故折线｜x－1｜＋｜x＋1｜＋｜y｜＝3围成的图形为六边形，其面积为2S梯形ABCD＝5．

（第20题）