解题思路：待定系数法—精英数学大视野·八年级2020

莱布尼茨是著名的德国哲学家、数学家和自然科学家，他是数理逻辑的先驱者，同牛顿一起被并称为微积分的创始人．

莱布尼茨有特殊的中国文化情结，曾主编介绍中国的《中国近况》，并向康熙皇帝建议成立“北京科学院”．他还把发现的“二进制”与中国的“易卦”相联系．

知能概述

在解答一些与多项式相关的问题时，先设定一些有待确定的系数，再依据已知条件确定相应字母系数的值，从而使问题得到解决的方法叫待定系数法．

如果化简后的两个多项式恒等，那么它们对应项的系数分别对应相等，这是待定系数法的理论基础．

待定系数法在因式分解、分式、代数式的恒等变形、函数等方面有广泛的应用．

待定系数法彰显了逆向思考、结构思维、方程思想．

问题解决

例1　如果2x2－3x－1与a（x－1）2＋b（x－1）＋c是同一个多项式的不同形式，那么＝________．

（“希望杯”邀请赛试题）

钻研数学——这是一种需要全部灵活性和刻苦耐劳的智力体操．

——维纳

化简

（青少年数学国际城市邀请赛试题）

解题思路　展开比较或赋值，建立a，b，c的方程组．

例2　如果x3＋ax2＋bx＋8有两个因式x＋1和x＋2，则a＋b＝（　）．

A．7　B．8　C．15　D．21

（美国数学邀请赛试题）

解题思路　原多项式的第三个因式必是形如x＋c的一次二项式，故可考虑用待定系数法或赋值法解．

例3　k为何值时，多项式x2－2xy＋ky2＋3x－5y＋2能分解成两个一次因式的积？

（天津市竞赛题）

解题思路　因k为二次项系数，故不宜从二次项入手，而x2＋3x＋2＝（x＋1）（x＋2），可得多项式必为（x＋my＋1）（x＋ny＋2）的形式．

例4　当p，m为何值时，多项式x3＋px－2能被x2＋mx－1整除？

（湖南省常德市竞赛题）

解题思路　因（x2＋mx－1）｜（x3＋px－2），故必存在一个因式f（x），使得（x3＋px－2）＝f（x）（x2＋mx－1），可设x3＋px－2＝（x2＋mx－1）（x＋a）．

例5　分解因式x4－x3＋4x2＋3x＋5．

分析与解　这是关于x的四次多项式，可考虑用待定系数法将其分解为两个二次式之积．

设　x4－x3＋4x2＋3x＋5

＝（x2＋ax＋1）（x2＋bx＋5）

＝x4＋（a＋b）x2＋（ab＋6）x2＋（5a＋b）x＋5．

比较等式两边同次项的系数，得

由①、③，得：a＝1，b＝－2，代入②式，②式也成立．

∴x4－x3＋4x2＋3x＋5＝（x2＋x＋1）（x2－2x＋5）．

待定系数法解题的一般步骤是：

（1）依多项式次数设定含待定系数的多项式；

（2）展开比较同次项系数，得含待定系数的方程组；

（3）解方程组，求出待定系数．

其中恰当的设定是关键，在可预知多项式结构的基础上，应使待定系数较少．

如例3，关于x，y的一次式一般形式是ax＋by＋c，若设成一般式，原式＝（ax＋by＋c）（dx＋ey＋f），则极大地增加了计算量．

又5＝（－1）×（－5），若设原式＝（x2＋ax－1）（x2＋bx－5），则所得的关于a，b的方程组无解．故运用待定系数法有时需要通过计算来排除某种分解不可能的情况，因而较繁．虽如此，待定系数法仍体现着解法的通用性．

例6　已知x5－5qx＋4r能被（x－c）2整除，求证：q5＝r4．

（浙江省宁波市竞赛题）

证明　设，展开比较两边同次项的系数，得

由①、②，得a＝2c，b＝3c2，代入③、④，得r＝c5，q＝c4．故q5＝r4．

逆向运算

若将两个或两个以上数学对象变为一个结果的运算称为正向运算，则把一个数学对象分为两个或两个以上对象的运算称为逆向运算．整数分解、因式分解、部分分式相对于整数乘法、多项式乘法、分式加减都是逆向运算．

例7　（1）已知，其中A，B为常数，则4A－2B＝________；

（“五羊杯”竞赛题）

（2）把化为部分分式．

对于（1），把右边通分，比较分子对应项系数；对于（2），因2x3－13x2－7x＝x（x－7）（2x＋1），故可设

1．已知（19x－31）×（13x－17）－（13x－17）×（11x－23）可因式分解为（ax＋b）×（8x＋c），其中a，b，c为整数，则a＋b＋c＝________．

（四川省凉山彝族自治州中考题）

2．已知m，n是实数，且当x＞2015时，恒成立，则m2－n2＝________．

（“希望杯”邀请赛试题）

3．若x4－x3＋kx2－2kx－2可分解为两个整系数二次式的积，则k＝________．

（湖南省邵阳市竞赛题）

4．设多项式P（x）的各项系数都是非负整数，且P（1）＝6，P（3）＝32，则P（2）的所有可能值为________．

（“华罗庚金杯”少年数学邀请赛试题）(www.xing528.com)

把一个真分式化为几个简单的真分式的代数和，称为将分式化为部分分式．解题的一般步骤是：

先将分式的分母分解因式，再依据分母的因式次数假设分解后的部分分式，然后用待定系数法解．

若分式的分母中含有因式（x－a）n，则相应的部分分式为

5．设f（x）是关于x的多项式，f（x）除以2（x－1），得余式3；2f（x）除以3（x＋2），得余式－4．那么，3f（x）除以4（x2＋x－2），余式是________．

（世界数学团体锦标赛试题）

6．若代数式x2－6x＋b可化为（x－a）2－1，则b－a的值是（　）．

A．5　B．4　C．3　D．2

（“希望杯”邀请赛试题）

7．如果a，b是整数，且x2－x－1是ax3＋bx2＋1的因式，那么b的值为（　）．

A．－2　B．－1　C．0　D．2

（江苏省竞赛题）

8．设a为常数，多项式x3＋ax2＋1除以x2－1所得的余式为x＋3，则a＝（　）．

A．1　B．－1　C．2　D．－2

（江苏省竞赛题）

9．多项式x12－x6＋1除以x2－1的余式是（　）．

A．1　B．－1　C．x－1　D．x＋1

（全国初中数学联赛题）

10．若2x3－hx＋k的两个因式是（x＋2）及（x－1），则｜2h－3k｜的值是（　）．

A．4　B．3　C．2　D．1　E．0

（美国高中数学考试题）

11．把化为部分分式．

（“五羊杯”竞赛题）

12．当m取何值时，多项式12x2－10xy＋2y2＋11x－5y＋m可以分解成两个一次因式的积？

（河南省郑州市竞赛题）

13．把多项式4x4－4x3＋5x2－2x＋1写成一个多项式的完全平方式．

（江西省景德镇市竞赛题）

14．已知（x－a）（x－4）－1能够分解为两个二项式x＋b，x＋c的乘积（b，c为整数），求a的值．

（甘肃省兰州市竞赛题）

15．已知多项式ax3＋bx2＋cx＋d能被x2＋p整除，求证：ad＝bc．

（浙江省温州市竞赛题）

16．求使是非零可约的最小自数n．

（国际数学奥林匹克试题）

17．已知多项式x3－x－a与多项式x2＋x－a有公因式，求a的值．

（湖北省鄂州高中自主招生试题）

18．已知关于x的三次四项式ax3＋bx2＋cx＋d，当x依次取1，2，3，4时，多项式的值分别是，求a＋b的值．

（“希望杯”邀请赛试题）

19．已知，其中a，b为常数，且ab≠2．

（1）若，试求k的值．

（2）证明：如果f［f（x）］也是常数，那么这个常数不能是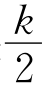，其中k如（1）中所述．

（青少年数学国际城市邀请赛试题）

例1　－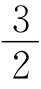

例2　D

例3　因x2＋3x＋2＝（x＋1）（x＋2），故可设原式＝（x＋my＋1）（x＋ny＋2），展开比较同次项的系数得k＝－3．

例4　设x3＋px－2＝（x2＋mx－1）（x＋a），即x3＋px－2＝x3＋（a＋m）x2＋（am－1）x－a，

1．－12　2．5　3．－1或1　设原式＝（x2＋mx＋1）（x2＋nx－2）或原式＝（x2＋mx－1）（x2＋nx＋2）．

4．13或16　因34＝81＞32，故P（x）的次数最高为3，设P（x）＝ax3＋bx2＋cx＋d，这里a，b，c，d都是非负整数，因P（3）＝32，故a＝0或1．

（1）当a＝0，则b＋c＋d＝6，9b＋3c＋d＝32，b≤3，又d＝3b－7，得b＞2，从而b＝3，d＝2，c＝1，P（2）＝16．

（2）当a＝1，则b＋c＋d＝5，9b＋3c＋d＝5，得b＝c＝0，d＝5，P（2）＝13．

5．5x＋4　设f（x）＝2（x－1）g（x）＋3，2f（x）＝3（x＋2）h（x）－4，3f（x）＝4（x2＋x－2）r（x）＋ax＋b，其中g（x），h（x），r（x）都是关于x的多项式，且次数均低于多项式f（x）的次数，f（1）＝3，f（－2）＝－2，3f（1）＝a＋b＝9，3f（－2）＝－2a＋b＝－6．

6．A

7．A　设原式＝（ax－1）（x2－x－1）＝ax3＋（－a－1）x2＋（1－a）x＋1，则b＝－a－1，1－a＝0．

8．C

9．A　设原式＝（x2－1）g（x）＋ax＋b，分别取x＝±1代入等式，得a＝0，b＝1．

10．E　设f（x）＝2x3－hx＋k，则f（－2）＝0，f（1）＝0．

11．原式＝，设原式

12．m＝2　因12x2－10xy＋2y2＝（4x－2y）（3x－y），故可设原式＝（4x－2y＋l）（3x－y＋n）．

13．原式＝（2x2－x＋1）2，可设原式＝（2x2＋ax＋b）2．