二次根式化简求值，精英数学大视野·八年级2020第8讲

这是奥地利1981年为纪念当年在奥地利因斯布鲁克召开的第十次国际数学会议而发行的邮票，它上面描绘的是一个“空间不可能体”，这形似四棱柱的几何体中充满了“不可能”，似是而非，自相矛盾．我们把这种画叫作悖论画，埃舍尔、彭罗斯创作的悖论画，其根源是“错误连接”．

知能概述

有条件的二次根式的化简求值问题是代数式的化简求值的重点与难点．这类问题涉及最简根式、有理化因式等重要概念，又包容了有理式的众多知识，同时联系着整体代入、分解变形、构造关系式等重要的解题技巧与方法．

问题解决

例1　（1）若实数a，b满足a2＋b2＝4，则＝________．

（华中师大一附中自主招生试题）

（2）已知＝2，那么的值等于_____．

（河北省竞赛题）

解题思路　对于（1），由条件及二次根式的概念，发掘a，b的值；对于（2），通过平方或分式性质，把已知条件和待求式的被开方数都用含x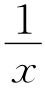＋的代数式表示．

正确的看法是，数学不仅拥有真，而且拥有非凡的美……是唯有最伟大的艺术才具有的严格的完美．

——罗素

无穷表达式

任何一个数都可以用连分数表示．

例2　已知，其中ab≠0，则的值为（　）．

（湖北省黄冈市竞赛题）

解题思路　将条件等式展开，作类似因式分解的变形，寻找a，b的关系．

例3　计算：

（1）

（江苏省竞赛题）

（2）

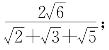
（全美中学生数学竞赛题）

（3）

（新加坡数学竞赛题）

（4）

（“华罗庚金杯”少年数学邀请赛试题）

解题思路　若一开始就把分母有理化，则使计算复杂化，观察问题中分子与分母的数字特点及被开方的数字间联系，通过分拆、分解、配方、一般化等方法寻找它们的联系，以此为解题突破口．

条件多样、形式多变是解二次根式化简求值问题的困难所在，构造法是突破这一难点的最有效方法，常见的构造手段有：

（1）构造基本对称式：x＋y，xy，再整体代入；

（2）构造零值多项式；

（3）构造倒数关系：x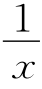＋或

（4）构造对偶式；

（5）构造图形等．

例4　（1）化简：

（北京市竞赛题）

（2）化简：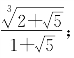

（江西省竞赛题）

（3）求满足的有序有理数对（x，y）．

解题思路　配方法（配成完全平方式或立方式）、待定系数法是化简复合根式的常用方法．

例5　设x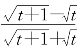＝，y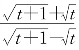＝，t为何值时，代数式20x2＋41xy＋20y2的值为2001？

（全国初中数学联赛题）

解题思路　整体代入x＋y，xy，建立关于t的方程．(www.xing528.com)

例6　已知实数x，y满足＝1，求证：x＋y＝0．

（俄罗斯数学奥林匹克试题）

分析　在证明一般性的过程中，由因导果，从化简条件等式入手，而化简的基本方法是有理化．

证明1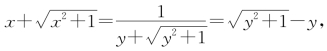

∴x＋y＝

两边平方并整理得

两边再平方得　x2y2＋x2＋y2＋1＝x2y2－2xy＋1，

即（x＋y）2＝0，故x＋y＝0．

对于一般式，利用待定系数法可得：

例6叙述简洁、结构优美、形式新颖．解题过程中所包含的知识简单，所运用的方法（平方、有理化）平常．把原题中的“1”变为一般常数，结论改变吗？读者不妨一试．

对本例进行变化与推广，可得到如下问题：

构造对偶命题

对于一个已知数式或一个已知命题，我们构造一个与之对应的数式或对应的命题，然后一起参与运算，从而使问题变得简单，这种解题方法称为构造对偶命题法．

例7　比大的最小整数是多少？

（西安交大少年班入学试题）

解题思路　直接展开，计算较繁，引入有理化因式辅助解题，即设x＝

有理化是解根式问题的关键，有理化的主要途径有：

（1）乘方：＝a；

（2）配方：＝｜a｜；

（3）对一个代数式分母有理化或分子有理化；

（4）在等式两边同乘有理化因式；

（5）引入一个有理化因式，一起参与运算．

1．已知，则2a3＋7a2－2a－12的值等于________．

（“《数学周报》杯”全国初中数学竞赛题）

2．已知（a是常数），则化简

（世界数学团体锦标赛试题）

3．若，则的值为________．

（合肥一六八中学自主招生试题）

拉马努扬（1887－1920），印度著名数学家，主要靠自学成才，是迄今为止最具洞察力的数学家之一，思维开阔，不拘于严密的逻辑推理，他给出的许多公式是借直觉推演而出．

他曾向印度数学会杂志提供了58个问题，其中的一些问题与根式相关．

形如的式子，怎样求其平方根？他给出了一种解决方法，并由此得出：

20．已知Rt△ABC的两条直角边长a，b和斜边长c都是正整数，且，求a＋b－c的值．

（世界数学团体锦标赛试题）

由（a，b）＝1，得（a2，b2）＝1，（9b2－a2，b2）＝1，从而（9b2－a2）｜64．

∵9b2－a2＝（3b＋a）（3b－a），9b2－a2≥0，∴9b2－a2＝8，16，32，64．

∵3b＋a，3b－a的和是6的倍数，其差为2的倍数，

∴（3b＋a，3b－a）＝（4，2）或（8，4）或（16，2），（a，b）＝（1，1）或（2，2）或（7，3）．

经检验（a，b）＝（1，1）或（7，3），故n＝1或11．

所以满足题设条件的Rt△ABC的三边长共有两组，分别为（a，b，c）＝（9，12，15），（a，b，c）＝（16，63，65）．

故a＋b－c＝9＋12－15＝6或a＋b－c＝16＋63－65＝14．