精英数学大视野：实数的性质及发展

负数概念的引入，数系扩张到有理数的范围；无理数概念的引入，数系扩张到实数的范围．实际的需要，数学本身的发展，需要产生新的数．

19世纪代数学最重大的事件之一是四元数的发现，它是由英国数学家哈密顿于1843年在皇家科学院宣讲的，形如a＋bi＋cj＋dk，其中a，b，c，d为实数．

知能概述

有理数与无理数统称为实数，全体实数和数轴上的点一一对应，实数有以下性质：

（1）有理数都可表示成分数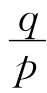（p，q是互质的整数，p≠0）形式．任何两个有理数之间有无穷多个有理数，有理数对四则运算是封闭的，即任两个有理数的和、差、积、商（除数不为0）还是有理数．

（2）无理数对四则运算不具有封闭性，即两个无理数的和、差、积、商不一定是无理数．

（3）设x为有理数，y为无理数，则x＋y，x－y，xy，都是无理数（x≠0，y≠0）．

问题解决

例1　若a，b满足，则的取值范围是________．

（全国初中数学联赛题）

解题思路　运用的非负性，建立关于s的不等式组．

在大多数科学中，后一代人往往撕毁了前一代人所建立的成就，但在数学中，每一代人都是在老的结构上建立新的成果．

——汉克尔·赫尔曼

神奇的π

π是一个常见的无理数，能用无穷多个数相加（无穷级数之和）来表示π．

莱布尼茨给出π的无穷级数表达式：

著名数学家赛尔伯格说：“这个公式实在美极了，奇数1，3，5，…这样的组合可以给出π．”

例2　下面有3个结论：

①存在两个不同的无理数，它们的差是整数；

②存在两个不同的无理数，它们的积是整数；

③存在两个不同的非整数的有理数，它们的和与商都是整数．

其中，正确的结论有（　）个．

A．0　B．1　C．2　D．3

（江苏省竞赛题）

解题思路　看能否举出符合要求的数．

例3　设等式在实数范围内成立，其中a，x，y是两两不同的实数，求的值．

（河南省竞赛题）

解题思路　根据算术平方根的意义，挖掘隐含条件a的值，寻找x，y的关系是解本例的关键．

例4　已知x，y都是有理数，且满足方程π＝0，求x－y的值．

（“希望杯”邀请赛试题）

解题思路　把原等式整理成有理数与无理数两部分，运用实数的性质建立关于x，y的方程组．

例5　设x，y为正有理数，为无理数，求证：为无理数．

（浙江省金华市竞赛题）

解题思路　正难则反，假设为有理数，通过运算，设法推出矛盾．

由算术平方根的定义可得到算术平方根的双非负性：

运用算术平方根的双非负性是挖掘隐含条件的常用方法．

实数有以下常用性质：

例6　已知在等式＝s中，a，b，c，d都是有理数，x是无理数，解答：

（1）当a，b，c，d满足什么条件时，s是有理数；

（2）当a，b，c，d满足什么条件时，s是无理数．

（“希望杯”邀请赛试题）

例7　一个问题的探究：

问题：设a，b，c为两两不相等的有理数，求证：为有理数．

（北京市竞赛题）

问题简证　设a－b＝x，b－c＝y，c－a＝z，则x＋y＋z＝0，xyz≠0．

由于a，b，c为两两不相等的有理数，所以，由有理数对四则运算的封闭性知原命题成立．

本质揭示　设实数x，y，z满足xyz≠0，且x＋y＋z＝0，

要证一个数是有理数，常证这个数能表示成几个有理数的和、差、积、商的形式；要证一个数是无理数，常用反证法，即假设这个数为有理数，设法推出矛盾．

题海茫茫，从一个典型问题出发，通过一般性、特殊化，例7展示了数学问题编拟的一个重要方法．

“这小小的苇笛，你携带着它逾山越谷，从笛管里吹出永新的音乐．”泰戈尔的诗句描绘了数学探究的优美意境．

估算与数感

随着无理数概念的引入，把数系扩张到实数的范围．有了实数，我们可以解高次方程，研究函数．数系的第二次扩张，为我们进一步学习代数开辟了广阔的领域．

数感是人们对数与运算的感觉与理解，主要表现为：理解数的意义，能用多种方法表示数，能把握数的大小关系；选择适当的算法，估算运算的结果；能运用数据表达来交流信息．(www.xing528.com)

例8　（1）已知m，n分别是的整数部分和小数部分，求n－m的值；

（2）设，b，c分别是a，a2的小数部分，求b（b＋c＋4）的值．

（全国初中数学竞赛题）

解题思路　原数＝整数部分＋小数部分，确定整数部分的方法是：找到与原数中被开方数相邻的两个平方数，借助估算求解．

1．若，则x2＋y2＝________．

（重庆市竞赛题）

2．设a＜b＜0，a2＋b2＝4ab，则的值是________．

（全国初中数学联赛题）

3．化简：

哲学家重视数学，而数学又始终影响着哲学．正与负、加与减、有理数与无理数、数与量、变与不变、相同与不同、偶然与必然、连续与离散、演绎与归纳、抽象与具体……没有数学与哲学，我们什么也看不透．

11．在黑板上写了若干个不同的数，它们中任意三个之和均为有理数，而任意两个之和均为无理数．则在黑板上写出的数的个数的最大值为（　）．

A．2　B．3　C．4　D．5

（北京市竞赛题）

（“希望杯”邀请赛试题）

13．设x为实数，使得如下四个数中恰有三个为整数：，求出这四个数．

（俄罗斯竞赛题）

14．开始时，黑板上写着三个实数每一分钟均擦去黑板上原来的三个数x，y，z，并写上x2＋xy＋y2，y2＋yz＋z2，z2＋zx＋x2三个数．问：能否在某一时刻，黑板上的三个数均为有理数？

（俄罗斯竞赛题）

（“祖冲之杯”竞赛题）

16．已知a，b为有理数，x，y分别表示为的整数部分和小数部分，且满足axy＋by2＝1，求a＋b的值．

（江西省南昌市竞赛题）

17．求证：

（1）一个自然数的平方被7除的余数只能是0，1，4，2；

（2）对任意的正整数n，不能被7整除（［x］表示不超过实数x的最大整数）．

（北京市竞赛题）

18．求证：平面上任意两个不同整点到的距离都不相等（整点是指横、纵坐标均为整数的点）．

（四川省竞赛题）

19．已知a，b，c都是有理数，也是有理数．证明：都是有理数．

（清华大学自主招生试题）

11．B　假设在黑板上写的数不少于四个，记这四个数为a，b，c，d，则a＋b＋c，b＋c＋d均为有理数，这表明，其差（b＋c＋d）－（a＋b＋c）＝d－a也为有理数．

类似的，b－a，c－a均为有理数．

因此，b＝a＋r1，c＝a＋r2，r＝a＋r3，其中，r1，r2，r3为有理数．

又a＋b＋c＝3a＋r1＋r2为有理数，于是，a也为有理数，这表明，a＋b＝2a＋r1为有理数，与“任意两个之和均为无理数”的条件矛盾．因此，黑板上写的数不超过三个，如

14．不能　考虑黑板上所写数的两两之差．

在一次操作中，差数x－y，y－z，z－x分别变为（x－y）（x＋y＋z），（y－z）（x＋y＋z），（z－x）（x＋y＋z）．

17．（1）设自然数m＝7q＋r（r＝0，1，…，6）．

则m2＝（7q＋r）2＝49q2＋14qr＋r2．

由于r2只能取0，1，4，9，16，25，36，被7除的余数对应为0，1，4，2，2，4，1．

因此，一个自然数的平方被7除的余数只能是0，1，4，2．

（2）由于n（n＋2）（n＋4）（n＋6）＝（n2＋6n）（n2＋6n＋8）（n＝1，2，…），

令k＝n2＋6n．则n（n＋2）（n＋4）（n＋6）＝（n2＋6n）（n2＋6n＋8）＝k（k＋8）（k≥7）．

18．假设结论不成立．则平面上存在两个不同的整点A（a，b），B（c，d）（a，b，c，d为整数），使得AP＝BP．

故AP2＝BP2．

由于式②的右边是整数，则必有（a－c）（b－d）＝0．③

（1）若a－c＝0，由式①知b－d＝0．此时，a＝c，b＝d．故点A与点B重合，矛盾．

（2）若a－c≠0，由式③知b－d＝0．从而，由式①知a－c＝0，矛盾．

综上，假设不成立．

所以，原结论成立．

若x＝0，则由①得a＝b＝c＝0，结论成立；若x≠0，y＝0，则由②得c＝0，矛盾；

若xy≠0，则由③得为有理数，矛盾．

综上，原命题成立．