式子
会随着n的增大而增大，当n无限增大时，
无限地接近于一个常数，这个常数就是欧拉数e，e是一个无理数，左图是它的近似值．
e是数学中最重要的5个常数之一，它如同圆周率π那样广泛出现在数学及其他各个领域中．
知能概述
分式方程即分母里含有未知数的方程，分式方程常转化为整式方程求解，但变形后的整式方程与原方程不是同解方程，解分式方程有可能产生增根，恰当运用增根是解分式相关问题的关键．
解复杂的分式方程常用到分式运算、分式的化简求值的策略与技巧．
问题解决
例1 若关于x的分式方程
的解是正数，则a的取值范围是________．
（黑龙江省竞赛题）
解题思路 x＞0且x≠2，这是本例的隐含制约．
（广西壮族自治区竞赛题）
解题思路 把第二个方程化为第一个方程的形式．
——汤姆森
最美的公式
eiπ＋1＝0
这是欧拉发现的公式，该公式将数学中5个重要的数1，0，π，e，i包含于一体，体现了数学的简洁奇异之美．
例2给出了形如
一类特殊分式方程的解，不解方程，应用方程解的定义可验证．
请你解下列方程：
例3 解下列分式方程：
（1）
（江苏省竞赛题）
（2）
（“希望杯”邀请赛试题）
解题思路 若去分母化为整式方程，则显然较繁．对于（1），分别计算左右两边；对于（2），把左边的每个分式拆项．
例4 解方程组：
（江苏省苏州市竞赛题）
解题思路 把各个方程两边取倒数，并从整体考虑．
例5 当a分别取－2，－1，0，1，2，3，…，97这100个数时，求关于x的分式方程
有解的概率．
（“希望杯”邀请赛试题）
解题思路 先求出使分式方程无解的a的值．
例6 求方程的
的正整数解．
（“希望杯”竞赛试题）
分析与解 易知x，y，z都大于1，不妨设1＜x≤y≤z，则
，将复杂的三元不定方程转化为一元不等式，通过解不等式对某个未知数的取值作出估计，逐步缩小其取值范围，求出其结果．
化分式方程为整式方程，是解分式方程最基本的思路，而解一些较复杂的分式方程常用到以下技巧：
（1）分步化简；
（2）拆项变形；
（3）巧取倒数；
（4）整体思考等．
从整式到分式，形象地说是从“平房”到了“楼房”．解分式问题总是在分式有意义的前提下进行的，具体反映在：
（1）舍弃增根而又会利用增根；
（2）剔除使分式无意义的未知数的值．
解与分式相关的不定方程问题，运用不等式，通过夹逼或放缩，确定一个未知数的取值范围，是一个重要的解题方法．
，即
，因此得x＝2或3，当x＝2时，
，即
，由此得y＝4或5或6；同理当x＝3时，y＝3或4，由此可得当1≤x≤y≤z时，（x，y，z）共有（2，4，12），（2，6，6），（3，3，6），（3，4，4）4组，由于x，y，z在方程中地位平等，可得原方程的解共有15组：（2，4，12），（2，12，4），（4，2，12），（4，12，2），（12，2，4），（12，4，2），（2，6，6），（6，2，6），（6，6，2），（3，3，6），（3，6，3），（6，3，3），（3，4，4），（4，4，3），（4，3，4）．
例7 河水是流动的，在B点处流入静止的湖中，一游泳者在河中顺流从A点到B点，然后穿过湖到C点，共用3小时．而由C到B再到A，共6小时．如果湖水也是流动的，从B流向C，速度等于河水速度，那么，这名游泳者从A到C只需2．5小时，问在这样的条件下，他由C到B再到A，共需多少小时？
（中国趣味数学大赛试题）
解 设游泳者的速度为每小时v1km，河水速度为每小时v2km．AB＝s1，BC＝s2，
由③得s1＋s2＝2．5（v1＋v2），④
由①得（s1＋s2）v1＋s2v2＝3v1（v1＋v2），⑤
由②得（s1＋s2）v1－s2v2＝6v1（v1－v2），⑥
由⑤、⑥得2（s1＋s2）＝9v1－3v2，⑦
由④、⑦消去s1＋s2得5（v1＋v2）＝9v1－3v2，⑧
即v1＝2v2， ⑨
于是
即由C到B再到A，共需7．5小时．
均值不等式
初中阶段，我们会遇到以下各种“平均”．
算术平均数：
调和平均数：
解较复杂的应用题，需增设未知数，以建立数量关系，设而不求，需要有较高的目标意识和较强的运算变形技巧．
可以证明下面关系式：
我们把这一系列与平均数有关的不等式称为“均值不等式”．
例8 上衣售价为40元一件、裙子售价为70元一条、鞋子售价为80元一双．小芳有800元，每种服饰她都至少买一件．若将一件上衣、一条裙子与一双鞋子称作一种搭配，两种搭配里只要有一项服饰不是同一件，就称作不同的搭配．请问小芳购买的服饰最多能做出多少种不同的搭配？
（国际中小学数学能力检测题）
分析与解 设小芳买了x件上衣、y条裙子、z双鞋子，则40x＋70y＋80z≤800，在此不等式条件下求xyz的最大值．
故xyz的最大值为84，此时，x＝7，y＝4，z＝3．
1．若关于x的方程
无解，则a 的值是________．(www.xing528.com)
（黑龙江省中考题）
2．关于x的方程
的解是正数，则m 的取值范围是________．
（重庆市竞赛题）
3．若关于x的分式方程
有整数解，则整数m的值是________．
（“希望杯”邀请赛试题）
4．若实数x，y，z满足
，则xyz的值为________．
（全国初中数学联赛题）
5．两组滑雪运动员共100人．从两组运动员中抽调15人组成一个小队，其中从第一组抽调的运动员的人数是这个组人数的p%，从第二组中抽调的人数是这个组人数的10%．原来两组滑雪运动员可能各有________人．
（欧拉奥林匹克试题）
以平衡视角探寻人类最质朴的智慧：数学是高等智慧生物的共有思维，是对真理的探索，对矛盾的怀疑；是常识的精微化．
6．若关于x的方程
的根为负数，则a的值为（ ）．
A．a≠－3 B．a≠3
C．a＜－1且a≠－3 D．a＞－1且a≠3
（华中师大一附中自主招生试题）
7．关于x的方程
有增根x＝1，则k的值等于（ ）．
A．2 B．3 C．6 D．10
（湖北省武汉市竞赛题）
8．某工程，甲队独做所需天数是乙、丙两队合做所需天数的a倍，乙队独做所需天数是甲、丙两队合做所需天数的b倍，丙队独做所需天数是甲、乙两队合做所需天数的c倍，则的值是（ ）．
A．1 B．2 C．3 D．4
（江苏省竞赛题）
（2）解方程组
（北京市竞赛题）
14．已知正整数x，y满足
＝a（a为正整数且x＜y），求x，y的值．
（江西省南昌市竞赛题）
15．某商场在一楼至二楼间安装一自动扶梯，以均匀的速度向上行驶，一男孩与一女孩同时从自动扶梯上走到二楼（扶梯本身也在行驶）．如果将男孩与女孩都作为匀速运动考虑，且男孩每分钟走动的级数是女孩的两倍，已知男孩走了27级到达扶梯顶部，而女孩走了18级到达顶部（设男孩、女孩每次只跨1级台阶）．
（1）扶梯露在外面的部分有多少级？
（2）如果扶梯附近有一从二楼下到一楼的楼梯道，台阶的级数与扶梯的级数相等，两人各自到扶梯顶部后按原速度再下楼梯，到楼梯底部再乘扶梯（不考虑扶梯与楼梯间的距离），则男孩第一次追上女孩时走了多少级台阶？
（江苏省竞赛题）
16．如图，在一条平直公路的前方有一陡峭的山壁，一辆汽车正以恒定的速度沿着公路向山壁驶去．
（第16题）
（1）若汽车的行驶速度是30米／秒，在距离山壁925米处时汽车鸣笛一声，则经过多长时间后司机听到回声？
（2）某一时刻，汽车第一次鸣笛，经过4．5秒再次鸣笛．若司机听到两次鸣笛的回声的时间间隔是4秒，求汽车的行驶速度．
（已知声音在空气中的传播速度是340米／秒）
（“希望杯”邀请赛试题）
17．已知
，x1＋x2＋…＋x1006＝5032，求x1006．
（克罗地亚数学竞赛题）
18．三名工人一起完成一项工程．开始时，第一名工人工作的时间为另两名工人一起工作完成整个工程的时间的一半；第二名工人工作的时间为另两名工人一起工作完成整个工程的时间的一半；最后，第三名工人工作的时间为另两名工人一起工作完成整个工程的时间的一半，此时他们能将整个工程完成．问：若一开始三名工人一起合作，则初始完成的时间是现在完成的时间的多少倍？
（爱沙尼亚数学竞赛题）
故原方程组的解为（x，y，z）＝（0，0，0），（1，1，1）．
例5 由原方程得（a＋1）x＝3a＋4 ①，当a＝－1时，方程①无解，原方程无解；
又原方程可能的增根是x＝1和x＝2，分别代入①得a＝－
和a＝－2．
故原方程有解的概率为
1．1或2
2．m＜－1且m≠－2
15．（1）设女孩速度为x级／分，电梯速度为y级／分，男孩速度为2x级／分，楼梯有s级，则
得
∴s＝54（级）．
（2）再设男孩第一次追上女孩时走过扶梯m遍，走过楼梯n遍，则女孩走过扶梯（m－1）遍，走过楼梯（n－1）遍，男孩上扶梯4x级／分，女孩上扶梯3x级／分．
得6n＋m＝16．
m，n中必有一个是正整数，且0≤｜m－n｜≤1．
显然，只能是m＝3，n＝2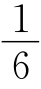
，即男孩向上走扶梯3遍，向下走楼梯2
遍，
故男孩所走级数＝3×27＋2
×54＝198（级），男孩第一次追上女孩时走了198级台阶．
16．（1）如图①，设经过t秒后司机听到回声，则30t＋340t＝2×925，解得t＝5．所以，经过5秒后司机听到回声．
（2）设汽车的行驶速度是v1，声音的传播速度是v2，汽车两次鸣笛的时间间隔是Δt1；汽车第一次鸣笛t1时间后，司机第一次听到回声；汽车第二次鸣笛t2时间后，司机第二次听到回声；汽车第一次鸣笛时，与山壁的距离为s．
如图②，如果司机先听到第一次鸣笛的回声，则有
两式相减，得2v1Δt1＝（v1＋v2）（t1－t2），即
（第16题）
司机两次听到回声的时间间隔是
代入数据，得
，解得v1＝20（米／秒）．
如图③，如果司机先听到第二次鸣笛的回声，同理，得
司机两次听到回声的时间间隔是
代入数据，得
，解得v1＝5780（米／秒）．
这样的速度不切合实际．所以，汽车的行驶速度是20米／秒．
18．不妨设三名工人单位时间里完成整个工程的百分比为x，y，z．于是，第一名工人的工作时间是另两名工人一起工作完成整个工程的时间的一半，为
类似的，有第二名、第三名工人的工作时间分别为
而三人一起工作，完成整个工程所需时间为
故初始完成工作的时间是三人一开始合作完成工作的时间的2．5倍．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
