八年级精英数学：分式化简求值

1614年，数学家纳皮尔引进了一种自然对数来作为数学计算的一种辅助手段，目的是用简单的加减法去代替含有乘除法的冗长计算，这极大地促进了天文学和航海学的发展．对数的发明导致了计算工具的产生，最早产生于1630年左右，之后被人们广泛使用了300多年，直至袖珍计算器产生．

知能概述

先化简后求值是解代数式化简求值问题的基本策略，分式的化简求值通常分为有条件和无条件两种情形．

解有条件的分式化简求值问题，既要瞄准目标，又要抓住条件；既要根据目标变换条件，又要依据条件来调整目标．

分式的运算是化简求值的基础，整式的变形、因式分解是工具，合理地通分是化解分式运算中难点的关键．

问题解决

例1　（1）若，则＝________；

（“希望杯”邀请赛试题）

（2）已知x2－x－1＝0，则＝________．

（广西壮族自治区竞赛题）

解题思路　对于（1），设出比值，引入参数；对于（2），由条件可得x2＝x＋1，x2－x＝1等，整体代入，不断地降低分子、分母的次数．

神奇化易是坦途，易化神奇不足提．

——华罗庚

欧拉公式

欧拉是18世纪瑞士著名数学家，他的贡献遍及高等数学的各个领域．同时，在初等数学中也到处留下了他的足迹，下面是关于分式的欧拉公式：

此公式整齐美观，左边的复杂与右边的简单给我们强烈的对比，一些分式的化简求值问题与上述欧拉公式有关联．

例2　（1）当x分别取值，1，2，…，2006，2007时，求出代数式的值，将所得的结果相加，其和等于（　）．

A．－1　B．0　C．1　D．2007

（全国初中数学联赛题）

（2）若a＋b＋c＝0，则的值是（　）．

A．0　B．1　C．－1　D．2

（湖北省黄冈市竞赛题）

解题思路　对于（1），取值成对互为倒数，不妨先计算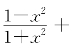对于（2），恰当运用条件，化多项式分母为单项式．

例3　化简：

（1）

（湖北省武汉市竞赛题）

（2）

（江苏省竞赛题）

（3）

（“五羊杯”竞赛题）

解题思路　不宜直接通分，运用分步通分、分组通分，先约分再通分，裂项相消后通分、换元等策略与技巧．

代数式的化简求值是一系列的变形与转化的过程，而变形应具有一定的目的性、方向性、针对性．目标意识、减少差异、消除差异有利于生成有序的逻辑推理．

例4　设a，b是实数，且满足，求的值．

（“希望杯”邀请赛试题）

解题思路　怎样运用条件？如何沟通条件与结论的联系？充分运用解与分式相关问题的技巧方法，可得不同解法．

例5　求最大的正整数n，使得n3＋100能被n＋10整除．

（美国数学邀请赛试题）

解题思路　由于n3＋100的次数高于n＋10的次数，所以，通过变形将整式整除的问题转化为一个分式的问题来加以解决，而解题的关键是把分式化为整式部分与分式部分的和．

例6　已知x，y，z满足＝1，求代数式的值．

（北京市竞赛题）

解题思路　用“直接代入法”或对已知条件作“整体变形”难以奏效，比较条件与结论，化整为零，分别把已知条件左边三个分式用其他两个分式表示．

解数学题是运用已知条件去探求未知结论的一个过程，充分运用已知条件是解题顺畅的重要前提，对已知条件的运用有下列途径：

（1）直接运用条件；

（2）变形运用条件；

（3）综合运用条件；

（4）挖掘隐含条件．

化分式为整式是解分式问题的常规思路，而有些整式问题可转化为分式的计算、化简，突破思维定式．取倒数、等式两边除以某因式、提取因式、字母化等是常见的转化方法．

例7　已知a，b，c为正数，满足如下两个条件：a＋b＋c＝32　①，②，求证：以为三边长可构成一个直角三角形．

（全国初中数学联赛题）

分析与解　由勾股定理，结论可表示为等式：a＝b＋c或b＝a＋c或c＝b＋a　③，联立①、③，只需证a＝1　6或b＝1　6或c＝1　6，即（a－1　6）（b－1　6）（c－1　6）＝0．　④

展开只需证明

0＝abc－16（ab＋bc＋ac）＋162（a＋b＋c）－163

＝abc－16（ab＋bc＋ca）＋163．　⑤

由①平方、移项，有a2＋b2＋c2＝322－2（ab＋bc＋ca），　⑥

又由②移项、通分，有

顺思逆想(www.xing528.com)

顺思与逆想是一种思考方法，一种提出问题、发展问题的方法，一种学习数学的基本功．运用它可使我们发现不同问题之间的联系，找到问题的内在规律与本质特征．

例8　（1）设，当A＋B＋C＝1时，求证：A1996＋B1996＋C1996＝3．

（天津市竞赛题）

大胆猜想，巧妙验证．例7的解法简单、自然．

“简单”，就是用简洁、明快、直接的方法解题．

“自然”，就是能把握问题的本质，朴实而不故弄玄虚．

著名棋手武宫正树，被人誉为“宇宙流”，他自己却说：“如果我给自己的围棋命名的话，是自然流．”又说：“只是非常自然地下”“下得自然、流畅就会感到美．”

对于例7，还有另一自然的证法：由a＝b＋c，b＝a＋c，c＝a＋b，只需证明［a－（b＋c）］×［b－（a＋c）］×［c－（a＋b）］＝0，读者不妨一试．

（2）若正数a，b，c满足求代数式的值．

（全国初中数学联赛题）

解题思路　由A＋B＋C＝1可推出A，B，C中有两个为1，一个为－1，解题的关键是由分式特点恰当配凑．问题（2）是（1）的逆问题，怎样切入？

怎样解题？怎样发现、创造数学的新命题？波利亚试图提炼出思考所遵循的路径，引导读者如何去思考问题、分析问题．

8．设实数a，b，c满足a＋b＋c＝3，a2＋b2＋c2＝4，则（　）．

A．0　B．3　C．6　D．9

（全国初中数学联赛题）

9．如果a＋b＋c＝0，＝0，那么（a＋1）2＋（b＋2）2＋（c＋3）2的值为（　）．

A．36　B．16　C．14　D．3

（湖北省武汉市竞赛题）

10．若实数a，b满足a－b＝2，＝4，则a5－b5＝（　）．

A．46　B．64　C．82　D．128

（全国初中数学联赛题）

11．考虑分数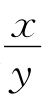（x，y为两个互素的正整数）组成的集合．若分子和分母均增加1，则分数的值增加10%．则这样的分数有（　）个．

A．0　B．1　C．2　D．3　E．无数多

（美国数学竞赛题）

17．已知实数a，b，c满足abc＝－1，a＋b＋c＝4，，求a2＋b2＋c2的值．

（全国初中数学联赛题）

18．设互不相等的非零实数a，b，c满足，求的值．

（全国初中数学联赛题）

19．已知非零实数x，y满足x3＋y3＋3x2y2＝x3y3，求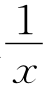＋的值．

（荷兰数学竞赛题）

20．求使得为有理数平方的所有整数n．

（荷兰竞赛题）

∴（c＋a－b）［c（a－b－c）－a（a＋b－c）＋b（c＋a＋b）］＝0，

（c＋a－b）（b＋a－c）（b＋c－a）＝0，

即a＋b－c＝0或b＋c－a＝0或c＋a－b＝0，

分别讨论可得A，B，C中有两个为1，一个为－1．

不妨设A＝1，B＝1，C＝－1，则A1996＋B1996＋C1996＝11996＋11996＋（－1）1996＝3．

（2）显然不能机械套用（1）的方法，但从（1）的解法中可作出猜测，如a＋b－c＝0，即c＝a＋b．由于a，b，c具有轮换对称性，不妨设0＜a≤b≤c，正难则反．

若c＞a＋b或c＜a＋b，则可推出与条件的矛盾，故c＝a＋b．从而原式＝1．

7．A　8．D

9．A　设a＋1＝m，b＋2＝n，c＋3＝p．

19．由已知方程得x3＋y3－x3y3＝－3x2y2，

（x＋y）3－x3y3＝x3＋3x2y＋3xy2＋y3－x3y3＝－3x2y2＋3x2y＋3xy2＝3xy（－xy＋x＋y）．①

应用立方差公式得

（x＋y）3－x3y3＝（x＋y－xy）［（x＋y）2＋xy（x＋y）＋（xy）2］＝（x＋y－xy）（x2＋y2＋2xy＋x2y＋xy2＋x2y2）．②

对比式①、②得

x＋y－xy＝0，③

或x2＋y2＋2xy＋x2y＋xy2＋x2y2＝3xy．④

又设4n－2＝cp2，n＋5＝cq2，c为整数．

得22＝4（n＋5）－（4n－2）＝c（2q－p）（2q＋p），22＝1×2×11，

∴2｜c（2q－p）（2q＋p），而2q－p与2q＋p奇偶性相同，2q＋p≥3，｜c｜＝2，

∴2q＋p＝11．

于是有：（1）若c＝2，2q＋p＝11，则2q－p＝1；

（2）若c＝－2，2q＋p＝11，则2q－p＝－1．

经讨论得p＝5，q＝3，n＝13，为此题的唯一解．