TRIZ经典解决问题流程

人类解决问题的过程非常复杂，涉及多学科和多领域，难以用简单的语言阐述清楚。当我们在工作中遇到具体的实际问题时，往往会先对问题进行详细分析，考察问题的属性，探究问题的根源，然后再着手去寻找解决问题的方法，最后提出解决方案。例如，对于某个实际问题，首先通过分析，将其定义为求解方程2x2-7x-9=0这个特定的数学问题。然后可以使用多种方法进行求解，如试凑法、配方法、直接开平方法、图解法等，但是通常经过分析后，我们会乐意选择求根公式法，将其转化为一个类似的数学标准问题：解一般化方程ax2+bx+c=0。接下来，运用该方程的标准解工具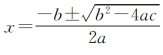，再类比到这个特定的数学问题之中，最后，求解得到这个方程的两个特定解：x1=-1，x2=4.5。显然，这个求根公式法的求解过程比试凑法、配方法、直接开平方法、图解法等的都要更快更准。

与此类似，人们在解决技术问题时，通常首先要对实际问题进行仔细的分析，找出关键所在；然后把这个关键问题转化为一个特定的问题模型；针对不同的问题模型，应用不同的解决工具，得到解决方案模型；最后，将这些解决方案模型应用类比到具体的问题之中，就是问题的最终解决办法。

TRIZ在解决发明问题的思维方法和解题流程上，与其他解决发明问题的方法的思路和流程基本相同，而二者的区别仅仅在于，TRIZ比其他解决发明问题的方法更加快捷、全面、准确和高效。

经典TRIZ理论解决发明问题的一般流程如图1.4所示。

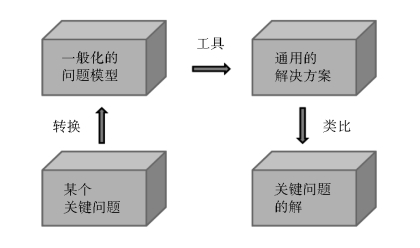
图1.4　TRIZ解决发明问题的一般流程(www.xing528.com)

①清楚地定义一个具体的关键问题。问题定义得越清楚，则解决问题的可能性越大，如果这个问题还没弄清楚，则需要将这个问题研究透彻后再着手解决。

②将这个待解决的关键问题转化为类似的标准发明问题模型，如技术矛盾、物理矛盾、物-场模型、How to模型等。

③针对不同的标准问题，运用不同的TRIZ问题求解工具，如矛盾矩阵及40个发明措施、四大分离原理、76个标准解、效应知识库等，得到通用的解决方案模型。

④将这些解决方案模型应用到这个具体的问题之中，通过类比，得到关键问题的解决方案。

在实际工作中遇到具体的发明问题时，可以利用上述某种标准问题求解方法，来寻求解决发明问题的途径。针对同一个问题，如果所建立的问题模型不同，使用的解题工具也会不同，因而得到的解决方案模型也将不同。从理论上来说，一般可以采用上述四种标准问题模型中的任意一种来寻找解决方案，但是，由于不同的方法解决问题的出发点是不同的，因而当面对一个具体问题的时候，应该先对问题进行分析，考察问题的属性，探究问题的根源，看看哪一种模型的方法更适合解决这个问题。只要具体问题具体分析，灵活应用不同的方法，便可以得到各种不同的备选方案，然后再从其中选择最好的解决方案。

对于一些复杂的、无法直接用以上工具解决的问题，TRIZ还提供了一套解决问题的流程和算法——发明问题解决算法（ARIZ），但是其求解过程相对比较复杂。