标准折现现金流模型假定,贴现率大小与未来现金流金额大小无关,但许多实证研究在改变实验中的现金流数额后,发现人们对大额现金流的贴现率通常低于对小数额现金流的贴现率(Thaler,1981;Loewenstein,1987;Benzion,Rapoport and Yagil,1989;Green,Fry and Myerson,1994;Kirby,Petry and Bickel,1999等),在行为经济学中称为“量级效应”。
例如,塞勒在研究中发现,被试对当前的15美元与1年后的60美元感觉无差异,同时对当前的250美元与1年后的350美元无差异,同时还对当前的3 000美元与1年后的4 000美元无差异。但通过计算可知,在这三种情形下的贴现率依次为139%、34%和29%,呈现出贴现率随现金流金额增大而降低的特征。
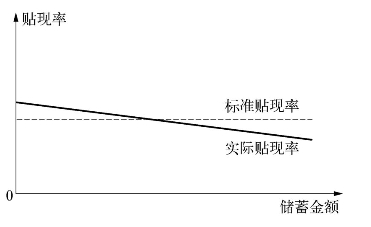
图9-2 储蓄金额对实际贴现率的影响
这说明,人们在进行储蓄决策时,储蓄金额越大,未来现金流入越高,要求的回报率可能就越低,如图9-2所示。人性果真如此,也会对人们的储蓄决策(和保险公司的储蓄性产品设计和销售)产生重大影响。(https://www.xing528.com)
其实,这一点在人身保险交易中已经有所体现。当客户看到长期储蓄性保险产品的利益演示表时,通过对比自己的储蓄金额和保险公司给付金额,往往会有如下感觉:储蓄金额越高,未来的给付金额自然就越高,自己对产品的满意度就越高。在实际收益率相同的情况下,客户对储蓄金额高的方案更满意,实际上就意味着:储蓄金额越高,客户要求的回报率就越低。这里以一个简化的即交即领年金保险为例来进行说明。
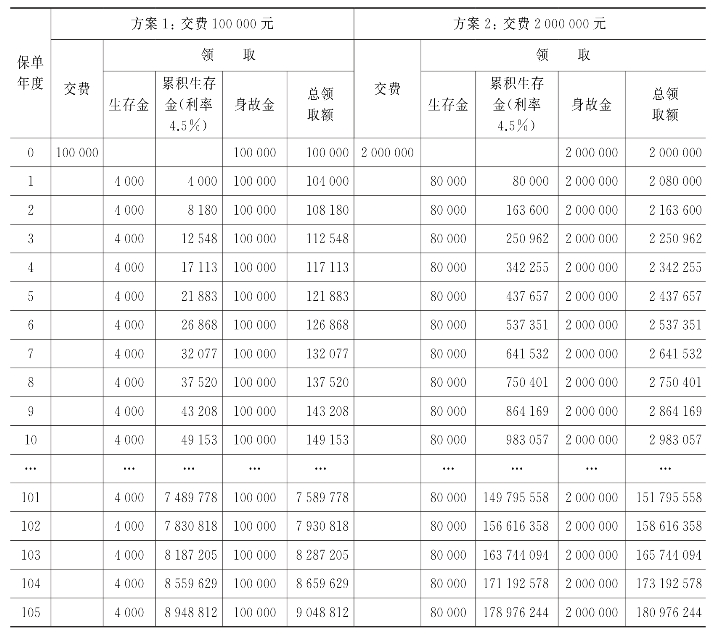
假设有一款某保险公司的固定利率即交即领型年金保险产品,保单规定:客户采取趸交保费方式交纳保费,从第一保单年度开始,每一保单年度末均领取金额为总保费4%的年金,直至被保险人身故为止,被保险人身故时返还所交保费。如果被保险人年龄为0岁,选择的交费规模分别为趸交10万元(方案1)或趸交200万元(方案2),忽略从保费中扣除的营销和管理费用,则两种方案下该保单的利益演示大致如表9-1所示。
面对上述两种方案,恐怕多数人会更喜欢方案2。由于方案1和方案2的实际收益率都是4%,因此,方案2的优势地位本身就显示出了所谓“量级效应”,即人们在进行储蓄决策时,储蓄金额越大,要求的回报率可能就越低。
表9-1 某简化年金保单的简化利益演示表 单位:元
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




