行为保险经济学：贴现率保持稳定与现实不符

标准的折现现金流模型假定，个体未来各期的贴现率r是固定不变的，但大量实证研究反复表明，个体的贴现率r是时期t的递减函数。这意味着人们对未来期限中的前期现金流的贴现率较大，对未来期限中的后期现金流的贴现率相对较小，反映出人们的一条普遍心理特性：人们对推迟眼前的事情更缺乏耐心，而对于推迟未来的事情却不甚关心。如此，人们对未来的看法就与标准模型的描述不同了。

例如，Ainslie和Haslam（1992）通过实验研究发现：绝大多数被试都表示，他们更偏好可立即兑付100美元的支票而不是2年后可兑换200美元的支票；但这些被试同时又表示，他们更偏好8年后可兑换200美元的支票而不是6年后可兑换100美元的支票。显然，被试们的前两年的贴现率大于第6年至第8年的贴现率

再比如，2017年诺贝尔经济学奖得主塞勒（Thaler，1981）曾通过问卷调查让被试回答：如果让被试推迟获得一笔应得的钱，那么被试需要获得多少钱才愿意。以当下获得15美元为例，等待时间（或延迟时间）分别为3个月、1年和3年时，被试们要求的获得金额的中位数分别为30美元、60美元和100美元。于是，经过复利公式计算得到：等待3个月、1年和3年的月度平均贴现率分别为26%、12.3%和5.4%。但是，等待1年的月度平均贴现率为12.3%其实意味着，如果最初3个月的月度贴现率为26%，则从第4个月到第12个月的月度贴现率肯定远低于26%；同理，等待3年的月度平均贴现率为5.4%其实意味着，如果最初1年内的月度贴现率为12.3%，则从第13个月到第36个月的月度贴现率肯定远低于12.3%。可以看出，被试们的贴现率是随时间递减的。

(www.xing528.com)

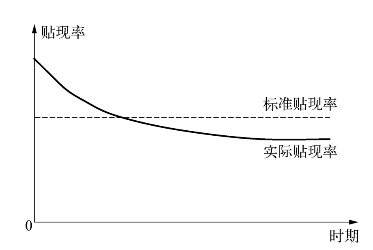
图9－1　前高收低的实际贴现率

大量实证研究都表明，随着时间延展，人们的贴现率前高后低，而非标准折现现金流模型所假定的始终如一的贴现率，如图9－1所示。据此，行为经济学家构建了双曲线贴现模型（如D（t）＝（1＋αt）－1等）和准双曲贴现模型（如D（t）＝1（当t＝0时）；D（t）＝βδt（当t＞0时））来描述现实世界的贴现行为。

不过，实际贴现率曲线是在标准贴现率曲线之上、之下还是如图9－1所示的与标准贴现率曲线交叉，在相关研究中看不到非常明确的结论。不过，从Frederick，Loewenstein and O’Donoghue（2002）对相关实验研究结论的综述来看，被试们在短期内（如几个月内或1年内）的贴现率普遍较高，高于同期的市场基准收益率，但对长期中后期的贴现率是否高于市场基准收益率，无法得到明确的结论。由于储蓄性保险期限很长，可以推断，个体的实际贴现率曲线与标准贴现率的相对位置，很可能是如图9－1有交叉点的样子。

这种对“眼前的未来”更缺乏耐心的人性，必然会对人们的储蓄决策（和保险公司的储蓄性产品设计）产生重大影响。例如，由于贴现率其实就是客户的要求回报率，而贴现率前高后低，就说明，一般投资者在进行长期储蓄决策时，希望长期储蓄产品的卖方最好能够提供前高后低的收益率，而非前后一致的收益率。这点肯定会让读者费解，一个储蓄性产品，其现金流入和流出确定后，就决定了一个唯一的内部收益率，卖方怎么能够在一个产品上提供前高后低的收益率呢？且看后面分解。