前景理论（Kahneman and Tversky，1979；Tversky and Kahneman，1992）主要包含两部分：价值函数和决策权重函数。价值函数类似于期望效用理论中的效用函数，但用决策权重函数取代了计算期望效用时的概率。
决策权重函数是客观概率的函数，描述了人们对概率的主观估计。卡尼曼和特沃斯基提出，人们会过于重视小概率事件，因此，当概率较小时，决策权重大于出险概率。在1992版前景理论的决策权重函数中，小概率与中高概率分界点为0.35。几乎所有保险承保风险的出险概率也低于0.35，因此，这里仅将P≤0.35的小概率部分的决策权重函数展示出来，如图5－11所示。
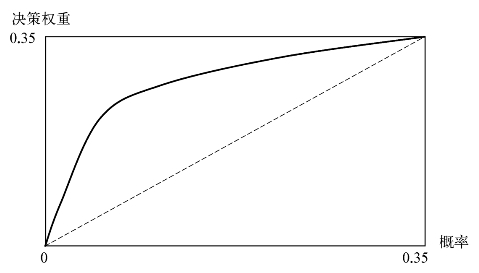
图5－11 小概率部分的决策权重函数
但是，在1979年版前景理论中，“人们会高估小概率风险”是在给定被试清晰的每项选择的结果概率分布后，根据被试的选择结果和价值函数形态（凹的还是凸的）推导出来的，并非被试对自身面临风险的主观判断结果。
例如，在问题8和问题8′中，
问题8：请在A和B中做出选择：
A：以0.002的概率获得3 000美元，以0.998的概率一无所获；
B：以0.001的概率获得6 000美元，以0.999的概率一无所获。
结果：绝大多数被试（73%）选择了B。
问题8′：请在C和D中做出选择：
C：以0.002的概率损失3 000美元，以0.998的概率损失为零；
D：以0.001的概率损失6 000美元，以0.999的概率损失为零。
结果：绝大多数被试（70%）选择了C。
针对问题8，人们倾向于选择B，意味着，
π（0.001）v（6 000）＞π（0.002）v（3 000）
再结合盈利区域价值函数是凹的，则(www.xing528.com)
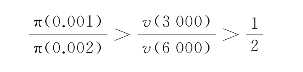
即，
，相对于准确估计小概率而言，人们仿佛会高估小概率风险。针对问题8′的结果，结合损失区域价值函数是凸的，可以得到相同的结论。
为了进一步证实“人们仿佛会高估小概率”这一结论，即当p较小时，π（p）＞p，卡尼曼和特沃斯基又使用了一组问题14和14′。
问题14：请在A和B中做出选择：
A：以0.001的概率获得5 000美元，以0.999的概率一无所获；
B：肯定获得5美元。
结果：绝大多数被试（72%）选择了A。
问题14′：请在C和D中做出选择：
C：以0.001的概率损失5 000美元，以0.999的概率损失为零；
D：肯定损失5美元。
结果：绝大多数被试（83%）选择了D。
针对问题14，人们倾向于选择A，意味着，
π（0.001）v（5 000）＞v（5）
在结合盈利区域价值函数是凹的，则
即，相对于准确估计小概率而言，人们仿佛会高估小概率。针对问题14′的结果，结合损失区域价值函数是凸的，可以得到相同的结论。[19]
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
