附加费率为零时的投保决策：足额保险

如前所述，消费者面临的投保决策思维框架可以描述为：“我的期初财富为W0，我现在有一笔新增收入I，如果购买保险，这笔新增收入正好等于最优保险购买量所需的保费，这笔新增收入也可用于购买其他商品。那么，我到底应该购买保险，还是购买其他商品呢？”

显然，当附加费率为零时，消费者购买保险的条件就变为

而且，若式（4－9）成立，消费者会将保额购买或增加至满足式（4－10）为止。

1.是否投保？

观察式（4－9），对应边际效用递减的财富效用函数，当附加费率为零时，以期初财富线（W＝W0）为界，多花1元购买保险带来的保险边际效用ΔU一定在期初财富线的左边（如图4－5），多花1元购买其他商品带来的其他商品边际效用ΔU′则一定在期初财富线（W＝W0）的右边（如图4－6）。显然，在效用函数呈边际效用递减的条件下，ΔU一定大于ΔU′。

简而言之，如果附加费率为零，消费者就是用现在的1元钱的效用去换出险后1元钱的效用，由于边际效用递减，站在决策点（W＝W0）来看，前者一定大于后者，这意味着，风险厌恶的消费者一定会购买保险。(www.xing528.com)

2.购买多少保险？

那么，消费者会购买多少保险呢？其实，在效用函数U（W）、W0和L已知的条件下，ΔU和ΔU′都是保额X的函数，而且，ΔU是X的减函数，ΔU′是X的增函数。

消费者刚开始购买保险，ΔU一定大于ΔU′，ΔU在期初财富线（W＝W0）的左侧，ΔU′在期初财富线（W＝W0）的右侧。随着保额X增加，ΔU逐渐减小并沿效用曲线向右上方迈进，ΔU′逐渐增加并沿效用曲线向左下方迈进。当然，两者向期初财富线（W＝W0）迈进的步伐是不对称的，右侧1元支出带来的ΔU′就是对应1元的收入效用，左侧1元保费支出对应远超1元收入的效用跳升，但在乘以出险概率p后，实际效用提升就变为ΔU了。当保额增加至足额保险（X＝L）时，ΔU从左侧到达了期初财富线，ΔU′则从右侧到达了期初财富线，两者几乎相等了。即当买到足额保险时，ΔU≈ΔU′。如图4－7所示。

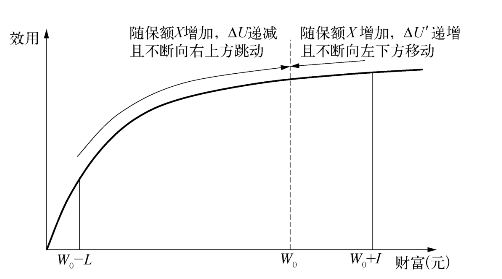
图4－7　随保额增加而变的保险边际效用和其他商品边际效用

而如果进一步扩大保额，购买超额保险，一方面保险公司很可能不同意，另一方面，购买超额保险将会导致ΔU到了期初财富线的右侧，ΔU′则到了期初财富线的左侧，对消费者而言是不合算的。

因此，在保险公司只收取纯保费的条件下，风险厌恶的消费者不但会购买保险，而且会购买足额保险。

正如平狄克、鲁宾费尔德（2000）在《微观经济学》中所述，人们之所以愿意投保，关键是因为，“财富从没有损失的情况下向有损失的情况转移一定会增加总效用，而这财富的转移正是通过购买保险来实现的。”