行为保险经济学：期望效用理论公理化

丹尼尔•伯努利发明期望效用理论后，1940年代，冯•诺依曼和摩根斯坦（vonNeumann and Morgenstern）将其进行了公理化^[2]，建立了公理化的期望效用理论。^[3]

冯•诺依曼和摩根斯坦首先为理性决策提供了一套明确的基本假设或者公理，这些公理主要包含：①有序性公理。即理性决策者可以对任意两个备选行动方案进行比较，结果是，要么偏好其中一个，要么对两个都无所谓；②占优性公理。即理性决策者永远都不会采取一个被其他行动策略占优的行动策略，所谓A策略比B策略占优，是指采取A策略一定比采取B策略更好，会带来更大的效用；③相消性公理。如果两个备选方案的行动结果都是不确定的，可能的结果中包含了一些数值相同且出现概率相等的结果（即两个概率分布中有部分完全相同），那么，理性决策者在对这两个方案进行选择时，应该忽略那些数值相同且出现概率相等的结果的效用，或者说两个方案的相同部分应该相互抵消；④可传递性公理。如果理性决策者在方案A和方案B中更偏好方案A（即A比B好），在方案B和方案C中更偏好方案B（即B比C好），那么这个人在方案A和方案C中肯定更偏好A方案；⑤连续性公理。对于任何一组结果，如果出现最好结果的概率非常大，那么，理性决策者总是偏好在最好和最坏的结果中进行赌博而不是选择一个中间值。例如，如果面临这样的选择，方案1的结果是确定地获得100元，方案2是以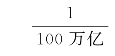的概率遭受巨额损失、以“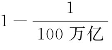”的概率获得1000元，理性决策者会偏好方案2；⑥恒定性公理。理性决策者不会受到备选方案的表现方式的影响。例如，面对本质上相同的一个复杂赌博（如两阶段彩票，第一、二阶段的获奖概率均为50%，两阶段均中奖则得到1000元）和一个简单赌博（如一次性彩票，获奖概率25%，获奖金额1000元），理性决策者肯定会认为两者无差异，而不是偏好某一个。

在定义上述公理的基础上，冯•诺依曼和摩根斯坦从数学上对期望效用最大化准则的合理性进行了论证，他们从数学上证明了，如果个体的偏好能够满足上述理性行为的基本公理，那么该个体所做出的决策就可以被认为达到了期望效用最大化。反之，如果决策者违背了这些公理，期望效用就无法达到最大化。(www.xing528.com)

由此，期望效用最大化被视为理性行为准则，因为它是由一些所有理性人都会接受的公理化原则推导出来的，是一套科学的理论体系。