组合图形面积计算-上海中学东校导学培优

上节课我们已经学习过如何求组合图形的周长.那么.如图4-20所示，我们怎样去计算阴影部分的面积呢？

在求组合图形周长时，我们采取的是将组合图形拆分或组合成几个比较规则的图形，分别计算其周长，然后再去求组合图形的周长，从而使问题得以解决.

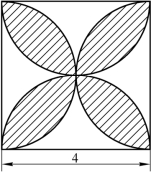
图4-20

那么，针对上述问题，我们是否可以采用类似的思路，将组合图形拆分或组合为几个规则的图形，然后再进一步去计算组合图形的面积呢？

我们可以这样来思考：阴影部分的面积等于两个直径为4的圆的面积减掉一个边长为4的正方形的面积，具体算法如下：

S阴影=2×π×22-42=8π-16≈9.12.（π≈3.14）

你还有其他的解决方法吗？试试看.

下面我们通过一些例题来研究如何求组合图形的面积.

容斥原理：在计数时，必须注意没有重复，没有遗漏.为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理.

例1 如图4-21所示，正方形ABCD 的边长为4厘米，分别以B，D 为圆心以4厘米为半径在正方形内画弧.求阴影部分的面积.（π≈3.14）

答：阴影部分的面积约为9.12平方厘米.

以上两个问题的解决，我们是将阴影部分的图形看做是两个或两个以上图形的重叠部分，然后运用“容斥原理”来进行解决.

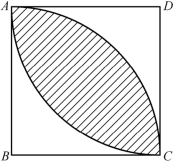
图4-21

例2 如图4-22所示，大正方形的边长为4厘米，每个小正方形的边长为2厘米.求阴影部分的面积.（π≈3.14）解法1 我们可以分别计算每部分阴影的面积，然后再乘以4.

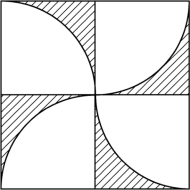
图4-22

解法2 我们可以将原图重新组合成一个图形，如图4-23所示，这样就可以很方便地求出阴影部分的面积.

S阴影=16-π×22≈3.44（平方厘米）.

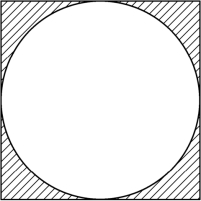
图4-23

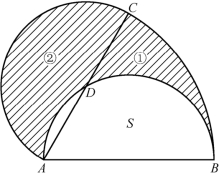
图4-24

例3 如图4-24所示，将直径AB为6厘米的半圆绕点A逆时针旋转60°，此时AB 到达AC 的位置.求阴影部分的面积.（π ≈

3.14）

分析 我们可以尝试通过割补的方法，将阴影部分拼成一个规则的图形.显然②号区域的面积等于S，于是可以将②的面积补到S区域，这样阴影部分就拼成了一个半径为6，圆心角为60°的扇形.

答：阴影部分的面积约为18.84平方厘米.

出入相补（又称以盈补虚）原理是中国古代数学中一条用于推证几何图形的面积或体积的基本原理.出入相补原理最早由魏晋时期数学家刘徽认识到其重要性并发展的.

例4 如图4-25所示，等腰直角三角形ABD 中，∠ADB=90°，AD=DB=1厘米，AC=厘米.求阴影部分的面积.

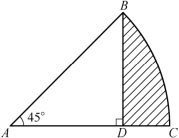
图4-25

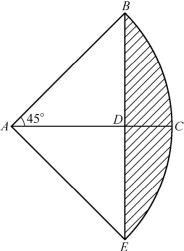
图4-26

分析 我们可以作出图4-25关于直线AC的对称图形，从而得到一个新的图形，如图4-26所示，再利用图4-26间接求阴影部分的面积.

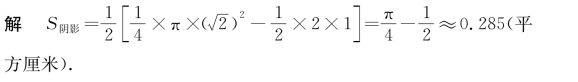
答：阴影部分的面积约为0.285平方厘米.

练习4.6(www.xing528.com)

1.如图所示，阴影部分的面积是____________.（π≈3.14）

（第1题）

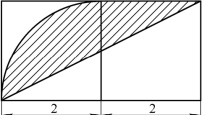
（第2题）

2.如图所示，阴影部分的面积是____________.（π≈3.14）

3.如图所示，阴影部分的面积是_______________.

（第3题）

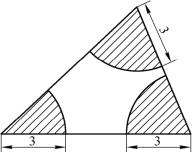
（第4题）

4.如图所示，求阴影部分的面积.（π≈3.14）

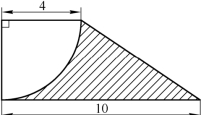
（第5题）

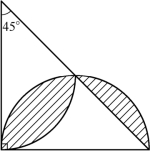
（第6题）

5.如图所示，求阴影部分的面积.（π≈3.14）6.如图，已知直角三角形的面积是12，求阴影部分的面积.（π≈

3.14）

阅读材料

不规则图形的面积测量与计算

同学们已经学习了规则图形以及组合图形面积的求法.在实际工作中，我们会遇到更多计算不规则图形的面积的问题.对于不规则图形的面积计算，基本思路是将曲边转化成直边，复杂图形转化成简单规则图形，然后进行计算.具体的方法有分割法、割补法与数方格计算法等.一般来说，这些方法都是近似计算方法.但是，由于生产建设中，需要提供的面积数量大小的精确度要求往往是不高的（少数情况例外），因此在一般情况下，这些近似计算方法已能满足实际工作的需要.

一、分割法

把一个不规则图形分割成（或近似地分割成）若干个规则图形来计算面积的方法叫作分割法.分割时可以采用作普通的辅助线或作系列平行线两种作图方法.

如图4-27所示，为了求一条河流在某处的横断面面积，我们将它分成10个图形，分别近似成三角形或者梯形.先求出每个图形的面积，再把它们加起来就行了.

图4-27

二、割补法

把一个不规则的图形割补成一个边数由折线组成的多边形，再来计算面积的方法，叫作割补法.对于边线是闭合曲线的地块，如果不能直接用分割法把它分割成规则图形，这时常常可以采用割补法.

使用割补法时，要注意以下两点：

（1）尽量使多边形的边数少一些；

（2）取直的直线往往要穿过曲线，这时总有一部分面积被割去，也有一部分面积做补进，割补时要尽量使割去的和补进的面积相等.

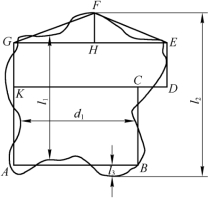
图4-28

如图4-28所示，为了测量这个不规则形状图形的面积，采用割补法.将该图形割补成多边形ABCDEFG.再将这多边形分割成两个长方形与一个三角形，测量出它们的有关边长，得到数据，再进行计算就可以了.

三、数方格计算法（方格法）

对于已给出其平面图的曲边形土地的面积，可以把印有方格的透明纸盖在图形上，然后通过数方格的个数来确定曲边形土地的面积.具体做法是：数出位于图形轮廓内完整的与不完整的格数，对不完整的格数一律以半格来计算（或用目估法将不完整格数凑成完整的格数）.从而求出图形所占的总格数=完整格数不完整格数.如果总格数为n，每格面积为a，那么S ≈na，如图4-29所示.

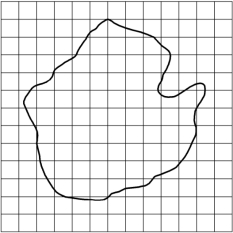
图4-29

同学们，看了以上方法之后，我们一起动动手测一测我们的校园（如图4-30所示）占地面积吧.

图4-30