我们已经学习过三角形、长方形、正方形、圆形、扇形等图形的周长计算方法，如图4-15所示，两个小半圆的半径均为3厘米，我们怎样去计算阴影部分的周长呢？
图4-15
我们注意到，阴影部分已经不再是前面所学的基本图形，不能简单地利用周长公式来进行直接计算.类似于这些，不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的图形，它们的面积及周长无法直接应用公式计算，一般我们称这样的图形为组合图形.
针对上面的问题，我们可以考虑将阴影部分的周长分割为一个半径为3厘米的圆的周长与一个半径为6厘米的半圆圆弧长的和.
下面我们通过一些例题来研究如何求组合图形的周长.
图4-16
答：阴影部分的周长为6π厘米.
以上两个问题的解决，我们都是将组合图形拆分成几个比较规则的图形，分别计算周长，然后再计算组合图形的周长.
如图4-17所示，三角形的三条边长都是27毫米.分别以A，B，C三点为圆心，27毫米为半径画弧，求AB︵+BC︵+AC︵的长.
图4-17
分别以等边三角形的每个顶点为圆心、以边长为半径，在另两个顶点间作一段圆弧，三段圆弧围成的曲边三角形称为勒洛三角形.
例3 如图4-18所示，有三根原木，其横截面均为直径为4分米的圆.如果把它们用铁丝捆在一起（接头不计），那么至少应准备多长的铁丝？
图4-18
分析 铁丝的总长度，相当于求图中组合图形的周长，而组合图形的周长相当于一个直径为4分米的圆的周长加上一个边长为4分米的等边三角形的周长之和.
解 l=π×4+4×3=12+4π（分米）.
答：至少应准备长为（12+4π）分米的铁丝.
例4 如图4-19所示，求阴影部分的周长.
分析 阴影部分的周长相当于两个半径分别为3和5的四分之三圆的周长与两条长度为2的线段长之和.
答：阴影部分的周长为12π+4.(www.xing528.com)
图4-19
通过上述几个例题的学习，我们能够感受到，求组合图形周长的基本思路，是将组合图形进行合理的分割与组合，先利用计算公式求某一部分的长度，然后再对所求得的周长进行和差运算，进而求出阴影部分的周长.
练习4.5
1.如图所示，这是一个由三个半圆组成的图形，尺寸如图中所示（单位：厘米），则其阴影部分的周长为________.（π≈3.14）
2.如图所示，三角形ABC的边长都为6厘米.分别以A，B，C三点为圆心，边长的一半为半径作弧，则阴影部分的周长是________.（π≈3.14）
（第1题）
（第2题）
3.如图所示，在半径为4厘米的圆内，有两个半径为4厘米的圆弧，则阴影部分的周长为________.（π≈3.14）
（第3题）
（第4题）
4.如图所示，矩形的长和宽分别为10厘米和6厘米，则阴影部分的周长为________.
5.制造弯形管道时，经常要先按中心线计算“展直长度”，再备料.下图是一段管道，其中直管道部分AB 的长为3000毫米，弯形管道部分BC，CD弧的半径都是1000毫米，∠O=∠O′=90°.计算图中中心虚线的长度.（π≈3.14）
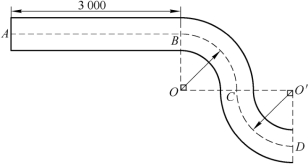
（第5题）
6.已知矩形ABCD的长AB=4，宽AD=3，对角线BD=5，按如图放置在直线AP上，然后不滑动，只转动.当它从A转动到A′时，顶点A所经过的路线长等于多少？ （π≈3.14）
（第6题）
7.如图所示是某学校田径体育场一部分的示意图.第一条跑道每圈为400米，跑道分直道和弯道，直道为长相等的平行线段，弯道为同心的半圆，弯道与直道相连接.已知直道BC的长为86.96米，跑道的宽为1米.（π≈3.14，结果精确到0.01）
（1）求第一条跑道的弯道部分AB︵的半径；
（2）求一圈中第二条跑道比第一条跑道长多少米；
（3）若进行200米比赛，求第六道的起点F与圆心O的连线FO与OA的夹角∠FOA的度数.
（第7题）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
