圆环的面积计算方法及答案

如图4-7，一个直径是30米的圆形牛栅，则牛能够活动的范围有多大？

圆的面积：圆所占平面的大小.

问题1 如何计算圆的面积呢？它与什么量有关呢？

圆的面积与直径有关，直径越大，则面积越大.

图4-7

问题2 你能估算直径是3厘米的圆的面积吗？

用正方形的面积来估计圆的面积.如图4-8所示，圆的面积大于小正方形的面积，小于大正方形的面积.

如果能将圆沿半径剪切拼成基本几何图形，则可计算面积.

操作

将一张圆形纸片剪切拼成近似的直线性图形.

沿半径将一个圆8等分，可拼出接

近平行四边形、三角形、梯形等图形，则可计算其面积.

沿半径将圆8等分、16等分，然后按图4-9的方法拼起来.

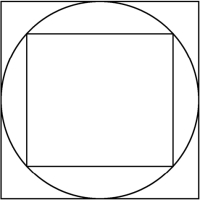
图4-8

思考：等分后，怎么拼图？

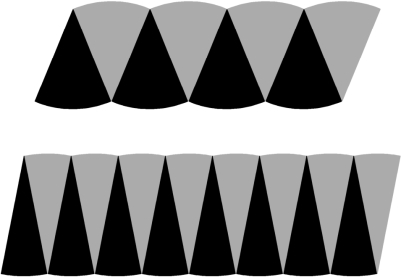
图4-9

思考：当等分的份数越多时，拼成的图形是什么？怎么计算面积呢？

通过观察和猜想，圆等分的份数越多，拼成的图形就越接近于一个长方形.长方形的长和宽分别是圆的周长的一半和半径.

思考：计算圆的面积时，蕴含了什么数学思想？

化曲为直和无限逼近的数学思想.

用字母S表示圆的面积，r表示圆的半径，则

例1 已知一个圆形桌面的直径为1.6米，求这个圆形桌面的面积.(www.xing528.com)

思考：如何测量圆形餐桌的面积？

测量直径.

例2 一台挂钟的时针长5厘米，求经过12小时后这根时针所扫过的区域面积.（π≈3.14）

解 ∵r=5，

∴S=πr2≈3.14×52=78.5（平方厘米）.

答：经过12小时后这根时针所扫过的区域面积为78.5平方厘米.

思考：时针扫过的区域是什么？

例3 圆环的外圆周长是18.84厘米，内圆周长是12.56厘米，求圆环的面积.（π≈3.14）

S环=S外-S内=πr2

外-πr2

内≈3.14×32-3.14×22=15.7（平方厘米）.

答：圆环的面积是15.7平方厘米.

思考：怎么计算圆环的面积？

练习4.3

1.圆的半径扩大到原来的4倍，下列说法错误的是（ ）.

A.直径扩大到原来的4倍

B.周长扩大到原来的4倍

C.面积扩大到原来的4倍

D.面积扩大到原来的16倍

2.一个圆形水池，它的周长是25.12米，求这个水池的面积.（π≈3.14）

3.把长和宽分别为4分米和3分米的长方形纸片剪成一个最大的圆，求这个圆的面积.

4.一个周长50.24米的圆形草坪的中心位置装有自动旋转喷灌装置，结果发现灌溉的面积只有78.5平方米.为了对整个草坪进行灌溉，灌溉装置的最大射程至少要增加多少米？（π≈3.14）

5.用两根同样长的铁丝，分别围成一个正方形和一个圆形，比较两个图形的面积大小.