上一节我们学习了分数和除法的关系,这节课我们进一步学习分数具有什么性质.我们仍然以几个生活中的常见问题作为问题的开始.

问题2 在下列□中填上合适的数:
你能把左边的除法改成分数形式吗?
(1)1÷4=(1×2)÷(4×□);
(2)2÷8=(2÷2)÷(8÷□).

思考:还有别的折法吗?如果有,比较分数所得出的结果是否一样.

图2-2
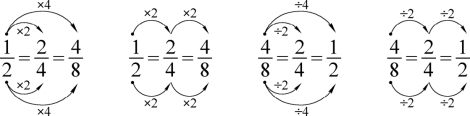
图2-3
你能从中发现什么规律?
根据图2-2和图2-3,这些分数的大小是相等的,即
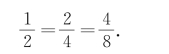
由分数和除法的关系以及除法的运算性质可得分数的基本性质:
思考:为什么分数会有这样的性质?
分数的分子和分母都乘以或都除以同一个不为零的数,所得的分数与原分数的大小相等.即
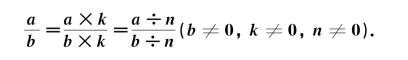
根据分数的上述性质,你能回答问题1吗?
例1 在括号内填上适当的数,使等式成立:
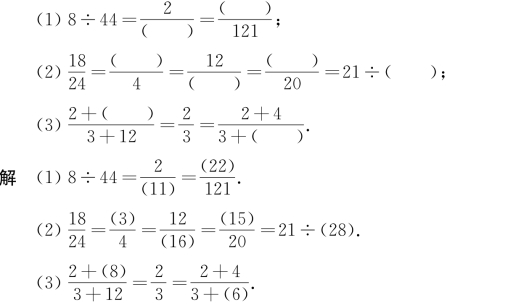
想一想:第(3)题该如何思考?

试一试:写出3个最简分数.
我们把分子和分母互素的分数,叫作最简分数(irreducible fraction),把一个分数的分子和分母的公因数约去的过程,称为约分(cancelling).通过约分可以化简分数.

根据约分的定义,只要除以分子与分母的公因数,即

例3 把下列单位换算的结果用最简分数表示.(https://www.xing528.com)
(1)125克是1千克的几分之几?
(2)400秒是多少小时?

把低级单位的单位名数改写为高级单位的单位名数,只要除以进率.把高级单位的单位名数改写为低级单位的单位名数,只要乘以进率.
例4 京沪高速铁路是一条连接北京市与上海市的高速铁路.现已知该高速铁路全长1318千米,某列高速试验列车全程共需行驶约3小时48分钟,那么这列高速试验列车平均每小时行驶多少千米?行驶1千米需要多少小时?
解 3小时48分钟=3.8小时.

两个问题需区分哪个量作为单位“1”.
例5 甲有苹果22个,乙有苹果18个,问:
(1)乙的苹果数占总苹果数的几分之几?
(2)若甲给乙6个苹果,则甲的苹果数是乙的苹果数的几分之几?
(3)当甲给乙多少个苹果后,甲的苹果数是乙的苹果数的![]() ?
?
注意:结果需用最简分数表示.

甲给乙苹果
![]()

练习2.2
![]()
2.填空题:

5.某班原有男生28人,女生20人,女生人数比男生人数少____________;后来又转来2位男生,则此时男生人数占全班人数的________.(填最简分数)
6.一条水渠全长48千米,已经修了40千米,__________________
________________________________________________
(在横线上填上适当的问句,编一道求一个数是另一个数的几分之几的题目,并说明理由).
7.七(3)班有45人,按要求每人至少要订阅《少年报》或《科技报》中的一种,其中30人订阅《少年报》,27人订阅《科技报》.问:
(1)订阅《少年报》的人数占全班人数的几分之几?
(2)订阅《科技报》的人数占全班人数的几分之几?
(3)两份报纸都订阅的学生人数占全班人数的几分之几?
(4)只订阅《科技报》的人数占全班人数的几分之几?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




