想一想 如何求一个正整数的所有因数?
例如:如何找出64和90的所有因数呢?
我们可以用64分别除以1,2,3,4,5,…,一直除到除数和商是同一个数时结束.另外,根据前面的学习,我们知道64不是3的倍数,也不是5的倍数,所以我们就不用去除以3和5.于是我们有64÷1=64,64÷2=32,64÷4=16,64不能被6和7整除,接着,64÷8=8.现在就不用往下除了,在这些算式中我们就可以找出64的所有因数:1,64,2,32,4,16,8(也就是算式中的除数和商).
同样,找90的因数时,我们有90÷1=90,90÷2=45,90÷3=30,90÷5=18,90÷6=15,90÷9=10,90÷10=9.这时除数和商交换位置了,我们就不用往下除了.
从以上方法我们可以看出,找一个数的所有因数,就用这个数从1开始去除,一直除到除数和商相同或交换位置,这些算式中的除数和商就是这个数的所有因数,重复的因数只写一个.
我们还可以用乘法算式的方法来找某些数的因数.例如:找出24的所有因数,我们就想哪两个数相乘的积是24:1×24=24,2×12=24,3×8=24,4×6=24.所以24的所有因数是1,2,3,4,6,8,12,24.
既然我们会求一个正整数的所有因数,那么一个正整数有几个因数呢?
找一个数的所有因数的方法不止我们现在介绍的这些,在随后的学习中,我们还有新的方法.
问题1 下列每个数各有几个因数?
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,…
因数只有一个的整数是__________________________________ .
因数有两个的整数是_____________________________________ .
因数有两个以上的整数是________________________________ .
一个正整数,如果只有1和它本身两个因数,这样的数叫作素数(primenumber);如果除了1和它本身以外还有别的因数,这样的数叫作合数(compositenumber).
例如:2,3,5,7,11,13,…都是素数;4,6,8,9,10,12,14,15,16,…都是合数.
从素数和合数的定义我们可知,素数的因数只有2个,合数的因数多于2个.
我们知道1只有它本身这一个因数,因此
1既不是素数,也不是合数.
之前我们学习过正整数按能否被2整除可以分为奇数和偶数,由以上可知正整数还可按因数个数分为1、素数和合数这三类.
注意:在素数中,2是唯一的一个偶素数,而奇素数却有无限多个.
因数和倍数、素数和合数、奇数和偶数是不同的概念,要注意区分.
试一试 判断题(正确的在题后的括号里打“√”,错误的打“×”).
(1)一个合数至少有3个因数.( )
(2)一个正整数不是素数就是合数.( )
(3)5的倍数一定是合数.( )
(4)所有的奇数都是素数.( )
(5)所有的素数都是奇数.( )
(6)所有的偶数都是合数.( )
(7)除了2以外任何一个正偶数都是合数.( )
(8)大于2的素数必为奇数.( )
问题2 奇数与素数、奇数与合数、偶数与素数、偶数与合数之间有什么区别和联系吗?
例1 判断21,31,43,57,85和91是素数还是合数.
解 21的因数有1,3,7,21;
31的因数有1,31;
43的因数有1,43;
57的因数有1,3,19,57;
85的因数有1,5,17,85;
91的因数有1,7,13,91.
通过检查每个数的因数的个数,可以知道31,43是素数,21,57,85,91是合数.
可以利用我们之前学习的整除的特征来判断:
21,57都能被3整除,所以除了1和它们本身这两个因数外,还有因数3,所以21,57是合数.
同样,85能被5整除,所以85也是合数.91是7的倍数,所以91也是合数.
思维拓展
通过上面的例题,我们如何判定一个正整数是素数还是合数呢?
素数的判定:
(1)查表法(https://www.xing528.com)
要判断一个数是不是素数,可以查看素数表.如果表内有这个数,那么它就是素数,否则就不是素数.
素数表的制作,可以用筛选法.同学们,下面让我们一起来制作100以内的素数表吧!
学习活动卡
表1-1是100以内的正整数.
表1-1 100以内的正整数
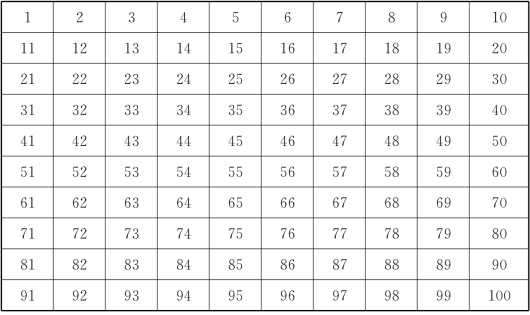
(1)1既不是素数也不是合数,故把1先划掉.
(2)剩余数中的第一个数2是素数,把它留下.把2后面所有2的倍数即偶数全部划掉.
(3)2后面第一个数3是素数,把它留下.把3后面所有3的倍数全部划掉.
(4)3后面没有划去的第一个数5是素数,把它留下.再把5后面所有5的倍数全部划掉.
……
这样继续下去,所有留下的素数就组成一张100以内的素数表.
同学们,请将你筛选出的100以内的素数填入表1-2.
表1-2 100以内的素数表

观察你制作出的素数表,你能总结出100以内的素数表的特点吗?
(2)试除法
如果没有素数表,可以用试除法来判断.
例如:判断197是不是素数.根据能被2,3,5,7,11,13整除的数的特征,我们可以判定197不能被2,3,5,7,11,13整除,接下来用17去试除:197÷17=11……10.此时商11比除数17小,说明197不可能有两个比17大的因数.如果197能被比17大的素数整除,那么所得的商一定比17小.但通过试除,比17小的素数都不是197的因数.因此我们可断定197只有1和它本身两个因数,即为素数.
又如:判断167是不是素数.通过试除我们知道167不能被2,3,5,7,11整除,接着我们用13去试除:167÷13=12……11.因为商12<除数13,且有余数,所以167是素数.
像上面这种判断一个数是不是素数的方法就是试除法.用由小到大的素数一个个去除,如果发现所给的数能被某一个素数整除,那么它就是合数;如果除到商比除数小还未能整除,就可断定所给的数是素数.
给定一个正整数,我们可以先根据经验,以及学习过的能被2,3,5,7等数整除的数的特征来试着判断一下它是否为合数,然后再考虑用查表法和试除法来判断它到底是合数还是素数.
练习1.5
1.在自然数1到20中,
(1)奇数有_________________,偶数有_____________________ ;
(2)素数有________________,合数有_____________________ .
2.在正整数中,
最小的素数是________,最小的合数是________,
最小的奇数是________,最小的偶数是________.
3.把30表示成2个素数的和________.
4.一个长方形的周长是16,且长和宽都是素数,则这个长方形的面积是________.
5.既是60的因数又是素数的有_______________.
6.在正整数中,1是( ).
A.最小的奇数B.最小的偶数
C.最小的素数D.最小的合数
7.在正整数中,4是( ).
A.最小的奇数B.最小的偶数
C.最小的素数D.最小的合数
8.判断题(正确的在题后的括号里打“√”,错误的打“×”).
(1)素数与素数的积一定是素数.( )
(2)能被1和它本身整除的数都是素数.( )
(3)两个素数的和一定是偶数.( )
(4)任意一个正整数至少有两个因数.( )
9.已知两个素数的和是40,求这两个素数乘积的最大值.
10.自然数123456789是素数还是合数?
11.连续九个自然数中至多有几个素数?
12.面积是72平方厘米的长方形,它的长和宽都是合数,则这个长方形的周长可能是多少厘米?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




