数一数,瞧一瞧,世界真奇妙!
图1-1
在日常生活中,我们经常需要计算物体的个数.在数的时候,用来表示物体个数的数1,2,3,4,5,…叫作正整数.
如图1-1所示,如果树上一只小鸟也没有,枝头上一个果子也没有,这时我们就说树上小鸟的只数是“0”,枝头上果子的个数是“0”.
零是一个数,记作“0”.在日常生活中,若没有物体,我们就用“0”表示,但这仅是零最初的含义.随着社会的不断发展,人类也赋予了零更多含义.零除了表示没有,还有以下我们常见的其他含义.
(1)表示数的某位上没有计数单位:如101,0.054中的0都表示某位上没有计数单位,即起到占位的作用.
(2)表示界限:如零上温度和零下温度以0摄氏度为界,向东、向西以原点0为界.
(3)表示起点:如刻度尺的起点刻度是0.
(4)用于编号:如邮编252000.
(5)表示概率:如一个事件发生的概率为0.
(6)表示精确度:如4.720表示精确到千分之一.
(7)记账的需要:如3元一般记作3.00元.
(8)在数的运算中零的作用举足轻重:如任何数与0相加,它的值不变;任何数减去0,它的值也不变;任何数与0相乘,积都为0;0作除数没有意义,故0不能作除数.
以后随着我们学习的深入,我们会对零有更进一步的认识.
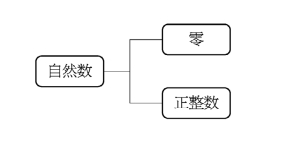
零和正整数统称为自然数(naturalnumber).
本章中学习的整数,在没有特别说明时,都是指正整数.
想一想 (1)有多少个自然数呢?(2)是否有最小的自然数?(3)是否有最大的正整数?(4)是否有最小的正整数? 六(1)班有36名同学.体育课上,王老师让体育委员组织同学排好队伍做操,要求每列人数相同.体育委员提出了以下5种排队的方案:
(1)排成4列;
(2)排成5列;
(3)排成6列;
(4)排成7列;
(5)排成8列.
你认为以上方案都可行吗?为什么?
解 (1)36÷4=9.
(2)36÷5=7……1.
(3)36÷6=6.
(4)36÷7=5……1.
(5)36÷8=4……4.
因为队伍要求每列人数相同,故方案(1)排成4列或方案(3)排成6列可行.
上面算式中的被除数和除数都是整数,它们的运算结果有什么不同?
问题
整数a除以整数b,如果除得的商是整数而没有余数,我们就说a能被b整除,或者说b能整除a,记作b|a.否则,则称a不能被b整除,或者说b不能整除a.
区别整除与除尽:
整除:(1)被除数、除数、商都是整数;(2)没有余数.
除尽:商是有限小数.
注意:整除可以理解为除尽的一种特殊形式.
用式子可以表达为:a÷b=c(a,b,c都是整数且b≠0),我们就说a能被b整除,或者说b能整除a.
在算式(1)(3)中,36能被4,6整除;也可以说,________能整除________.
而在算式(2)(4)(5)中,36不能被5,7,8整除;也可以说,_________________不能整除________.
例1 下列哪一个算式的被除数能被除数整除?
(1)17÷3; (2)36÷4; (3)15÷10.(https://www.xing528.com)
解 (1)17÷3=5……2.
(2)36÷4=9.
(3)15÷10=1……5.
所以,被除数能被除数整除的是算式(2).
例2 3.4÷1.7=2,可以说3.4能被1.7整除吗?解 因为被除数和除数都不是整数,所以不能说3.4能被1.7整除.
注意整除的条件:
(1)被除数和除数都是整数;
(2)被除数除以除数,商是整数而且没有余数.
想一想
整除有以下常用的性质(a,b,c均为正整数):
(1)若a|b,b|a,则a=b.
(2)若c|b,b|a,则c|a.
(3)若b|a,k为正整数,则b|ka.
(4)若c|a,c|b,则c|(a±b).
你能说明以上性质为什么成立吗?
在学习了互素的概念后,我们还会继续补充整除与互素有关的性质.
思考:小明同学根据整除的性质第(2)条得到一个类似的结论:若a不能被b整除,b不能被c整除,则a不能被c整除.你认为他的说法对吗?为什么? (1)0能被任何不为0的整数整除吗?
(2)任意一个自然数都能被1整除吗?
(3)m÷n=3,n一定能整除m吗?
练习1.1
1.从下列数中选择适当的数填入相应的横线上.
![]()
正整数:_________________; 自然数:_________________.
2.判断题(正确的在题后的括号里打“√”,错误的打“×”).
(1)2.5能被5整除.( )
(2)0是自然数.( )
(3)12能被1整除.( )
(4)4能整除2.( )
3.填空题:
20能被_____________整除, ___________能整除15.
4.在下列各组数中,第一个数能被第二个数整除的有________组.
17和34, 0.5和5, 17和3,
0.2和4, 20和5,18和3.
5.在下列各组数中,为四个连续的自然数的是( ).
A.0,1,1.5,2B.0,1,2,3
C.6,8,10,12D.3,5,7,9
6.请将下列12个数中存在整除关系的数一一找出,并写出整除关系式,例如:4÷2=2.
4,2,6,3,8,10,5,12,16,20,24,15.
7.求50以内被6整除的所有数的和.
8.64能被a整除,写出所有符合条件的a.
9.既能整除12又能被2整除的数有哪些?
10.96名同学报名参加“垃圾分类”志愿者活动,需平均分成若干组,且每组不少于4人,也不多于6人,应怎样分组?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




