哈勃定律发现与宇宙演化极简科学史

我们前面已经提到，假如宇宙是无限的，均匀和静态的，宇宙中分布着无限个恒星，则我们无论从哪个方向观看天空，视线都会碰到不止一颗恒星，因而整个天空看上去就会亮得像太阳一样。而实际上，如我们所知，不仅夜晚天空是黑暗的，而且即使白昼天空也不是像太阳一样耀眼，此即著名的奥伯斯之谜（图3.5）。为了解释这一现象，天文学家提出了各式各样的假说，有人用天体分布的非均匀性、天体寿命的有限性或演化效应来解释；也有人假设引力常数随距离增大而减小来解释等等。事实上，奥伯斯现象是把天文观测与理论推断相联系，在考虑宇宙的大尺度空间性质时提出来的。它标志着科学的宇宙学的萌芽。

广义相对论建立后，爱因斯坦即用其考察宇宙结构问题。1917年，他发表了“根据广义相对论对宇宙学所作的考察”一文，这是现代宇宙学的奠基之作。在这篇论文中，爱因斯坦假设，从大尺度来考虑，宇宙空间和物质分布是均匀的和各向同性的。这一假设经过苏联科学家弗里德曼的发展，后来被称为宇宙学原理。由于当时的天文观测只是初步发现旋涡星云的谱线红移现象，天文学界并未形成宇宙膨胀观念，基于他的均匀各向同性假设，爱因斯坦通过求解广义相对论引力场方程，并且引入宇宙常数项，建立了一个“静态、有限、无界”的宇宙模型。所谓静态，是指从大尺度来考察，宇宙空间中的物质基本上是静止不动的；所谓有限无界，是指我们的宇宙空间是三维的黎曼空间，它的大小有限，光线在这个空间内沿弯曲路径传播，始终不会有它的终点，即这个空间没有边界。爱因斯坦的这种研究，开辟了以广义相对论为基础的现代宇宙学研究的新时代。

图3.5　奥伯斯之谜，若宇宙是无限的，O处观察者的每一视线迟早将会遇到恒星或星系，所以天空必定是明亮的。

继爱因斯坦之后，荷兰天文学家德西特也于1917年利用爱因斯坦引力场方程提出了一个静态宇宙模型，但他认为宇宙的物质不是静止的，而是有运动，不过物质的平均密度趋近于零。

爱因斯坦在提出他的宇宙模型时，为了获得静态解，人为地在广义相对论引力场方程中增加了具有斥力性质的“宇宙项”。他认为宇宙中引力与斥力达到平衡时即处于静态状况，但如何说明“宇宙项”的物理基础，却是一个令人头痛的问题。1922年，苏联科学家弗里德曼重新求解了爱因斯坦引力场方程，并且未像爱因斯坦那样人为地引入“宇宙项”，结果发现，这一方程既存在着如爱因斯坦模型和德西特模型那样的静态解，也存在着两类膨胀解和一类振荡解，由此他建立了著名的弗里德曼宇宙模型。他还认为，爱因斯坦在场方程中引入“宇宙项”的做法是完全不必要的。根据弗里德曼模型，宇宙永远处于运动状态，它或者无限地膨胀下去或者膨胀和收缩交替进行（即做振荡运动）。宇宙究竟是单调膨胀还是不断振荡？人们对弗里德曼模型作了进一步研究后发现，关键在于宇宙物质的平均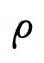密度与临界密度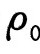的比值。如果宇宙平均密度小于临界密度，即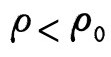，则宇宙空间曲率为负，对应于一个双曲型的开放宇宙，宇宙会一直膨胀下去；如果宇宙平均物质密度与临界密度相等，即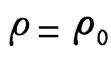，则宇宙空间曲率为零，对应于一个欧几里得的平直的开放宇宙，这种情况下的宇宙也会一直膨胀下去；如果宇宙平均物质密度大于临界密度，即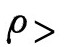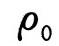，则宇宙空间的曲率为正，对应于一个没有边界的、体积有限的闭合宇宙，即宇宙膨胀到一定时候会收缩，然后再重新开始膨胀，形成膨胀、收缩、再膨胀、再收缩的振荡形式（图3.6）。

图3.6　开、平、闭三种宇宙模型的弗里德曼膨胀曲线。开放宇宙永远膨胀，闭宇宙膨胀后会再次收缩

我们生活于其中的宇宙会不断膨胀，或者到了一定时候还会收缩，由此意味着宇宙有个开端，或者还有末日，这太奇妙了！这个结论是在人们还没有发现宇宙膨胀的充分事实的情况下作出的。在传统观念上，人们习惯于认为宇宙在时间上是无始无终的，在空间上是无限的，否则怎样想象宇宙创生之前或宇宙末日之后的情景呢？所以人们乐于接受静态的、永恒的宇宙模型。弗里德曼模型在观念上如此新颖，以致爱因斯坦在开始时对其正确性也表示怀疑，但很快他即认识到了弗里德曼这一工作的重要意义，他甚至认为自己在引力场方程中引入“宇宙项”的做法是愚蠢的。弗里德曼模型的一系列奇妙结果都是通过求解广义相对论引力场方程得出的自然结论，不存在任何人为的假设，因此在未得到天文观测检验之前，人们虽然没有理由肯定它，但也同样没有理由否定它。在科学认识活动中，只要是正确的东西，它总会被越来越多的事实所证明。

1927年，比利时天文学家勒梅特通过求解广义相对论引力场方程也获得了一个膨胀宇宙模型，据此他把天文学家观测到的河外旋涡星系退行现象，解释为宇宙膨胀的结果。前面说过，爱因斯坦的宇宙学模型是静态的。当时他认为宇宙在大尺度上的特征是不随时间变化的，正因如此他才有意识地设法得到静态解。弗里德曼和勒梅特都证明，爱因斯坦的宇宙学模型是不稳定的，只要出现扰动，就会破坏平衡，使宇宙空间一直膨胀下去。所以，根据广义相对论所建立的宇宙学模型，本质上是动态模型，正如弗里德曼和勒梅特两人所建立的模型那样，它揭示了宇宙空间的膨胀属性。实际上，随着河外天文观测的进步，越来越多的事实也充分证明了我们生活的宇宙正在不断膨胀着。

有关宇宙膨胀的第一个观测上的启示，来自对旋涡星系的径向速度（即沿观测视线方向的速度）的早期测量。1842年，奥地利物理学家多普勒研究声音的传播时，发现了一种常见的效应。譬如当我们坐在火车里，如果对面有飞驰而来的火车，它的汽笛声就会突然变得很尖锐刺耳；但火车开过身旁而远去时，汽笛的声调便一下子低沉下来。这是由于当声源向着我们运动时，我们的耳朵接收到的声波频率将高于声源频率；当声源背离我们做后退运动时，我们耳朵听到的声波频率将低于发射频率，这种现象称为多普勒效应。多普勒还指出，光的传播应该具有和声波相同的行为。换言之，倘若光源退离观测者，则观测到的光的频率应该减小。由于光的颜色由其频率决定，所以频率的下降将会导致其颜色看上去变红了，此即所谓的多普勒红移。这一原理对于观测天体的径向运动情况很有价值。由于光的频率变化效应远远小于声音的频率变化，所以实际上光源颜色的变化很微小，难以据此准确判断光源的运动情况。后来人们发现，运用光谱分析方法可准确测定恒星的多普勒红移情况，也即恒星的径向运动情况。因为特定的谱线是由特定类型的原子所产生的，所以可以把恒星光谱中某一谱线的频率与实验室中同种原子所产生的该谱线频率加以比较，即可求出频率变化量，由此推算出恒星的径向速度。1914年，洛威尔天文台的斯利弗观测了十几个旋涡星系都在以大约每秒100英里到200英里的速度背离我们退行，但其中也有少数旋涡星系以很高的速度向我们接近。在随后的几年中，斯利弗观测到的具有径向运动的旋涡星系数目不断增加。这类现象意味着什么？天文学家当时还难以说清楚。1923年，英国天文学家爱丁顿针对这种情况指出，宇宙演化学的最令人困惑的问题之一，就是旋涡星系的巨大速度。但不久，这种困惑就被美国天文学家哈勃的出色工作所解决（图3.7）。(www.xing528.com)

1924年，哈勃利用当时世界上最大的反射望远镜观测旋涡星系之一的仙女座星系，结果发现它位于银河系之外，是和银河系一样的恒星系统，并非是一片模糊不清的星云。由此人们推测所有的旋涡星系都是位于银河系之外的恒星系，从而揭开了探索大尺度宇宙的新篇章。

1927年，荷兰天文学家奥尔特根据观测资料证实了银河系具有自转运动的假设，从理论上推导出银河系自转对恒星视向速度影响的公式，由此人们发现太阳和银河系中的其他天体也在绕着银河中心转动。考虑到银河系和太阳系的运动，必须对斯利弗观测的河外旋涡星系径向速度作某种修正，修正后的速度真实地反映了它们的运动状况，这使得人类对遥远宇宙天体的运动情况有了进一步的认识。

图3.7　哈勃

在上述认识基础上，1929年，哈勃经过对24个已知距离和视向速度的河外星系的分析研究，惊奇地发现，各星系都在背离我们而后退，它们退行的速度并非是杂乱无章的，而是遵循其视向退行速度与其距地球的距离成正比的关系，即星系离地球越远，其视向退行速度越大，用公式表示为V=HD，式中V是星系退行速度，D是距离，H是哈勃常数，此即著名的哈勃定律。

哈勃定律说明了星系红移现象的规律，红移越大，星系的退行速度越大，其距离地球也越遥远。由此证明，宇宙正在不断地膨胀着。这一结论与广义相对论的膨胀宇宙模型是一致的，是对膨胀宇宙论的有力支持。

为什么会造成河外星系的普遍退行呢？为了理解这一现象，可以把我们所处的宇宙空间设想为一个三维球面，并使它像一个正在被吹胀的气球一样膨胀。如果在球面上画着许多小点，当气球膨胀时，气球表面各点会相互散开。一个观察者站在气球上任何一点观看，其余各点都在远离他而去，而且他将发现，离他越远，各点的退行速度也越大。这种现象在球面上哪一点来看都是一样的（图3.8），这也形象地说明了宇宙是没有中心的，是均匀各向同性的。如果把星系看作气球上的点，那么可以看出，我们所能观测到的最遥远的天区，都处在膨胀之中，所以，是宇宙的膨胀造成了星系的系统性红移现象及普遍退行。

图3.8　宇宙的膨胀可用气球的膨胀作类比。气球上每一个斑点都可以认为自己是膨胀的中心