反比例函数与图形面积教学案例设计

1.课题名称：反比例函数与图形面积教学案例设计

2.教学目标：

（1）了解反比例函数式中的k的几何意义，理解反比例函数与图形面积的内在联系，掌握运用数形结合法双向解决反比例函数与图形的面积数学问题。

（2）在解决问题的过程中，体会数形结合思想在数学应用中的重要地位，经历探索反比例函数与图形面积的内在联系，体会函数的思想与建模的思想在数学问题中的运用。

（3）在小组交流学习活动中学会与人合作获得成功的体验，培养学生的合作意识和乐于探究的良好品质；在探究活动中培养学生学会观察、分析、归纳的能力；在问题变式中感受函数图像的简洁美，激发学生学数学的兴趣。

3.教学重难点：

教学重点：探索反比例函数式中的k与图形的面积联系。

教学难点：分析图像中信息来确定k与图形面积的关系。

4.教学过程

（说明：截取利用超级画板设计的教学片段，省略其他教学片断。）

（1）教学片段一：回顾反比例函数的性质

教师：拖动点k，改变k值，观察函数图像与k值的关系？

学生：当k＞0时，函数的图像分布在一、三象限；当k＜0时，函数的图像分布在二、四象限。

教师：在每一象限内，分别拖动点P，与点P观察yP，随xP的变化情况，观察yP随xP的变化情况。

学生：当k＞0时，在每支函数图像上y随x的增大而减小；当k＜0时，在每支函数图像上y随x的增大而增大。

设计意图：利用超级画板合理设计，通过动态操作演示，直观而形象地展示反比例函数，让学生在动态的数学实验环境中感受数形结合的思想方法。

（2）教学片段二：反比例函数与图形面积（矩形）

教师：用超级画板画出反比例函数y=的图像，通过标尺改变k的大小，在函数图像上取一点P，过P做PA⊥x轴，PB⊥y轴，得到矩形OAPB。当k＞0时，拖动点P（或点击“动画”按钮），同学们思考在这一过程中P点坐标、k值、矩形OAPB的面积的变化？

学生：在拖动P点过程中P点横纵坐标的乘积不变，等于k，矩形OAPB的面积等于k。(www.xing528.com)

教师：请同学们，打开超级画板自己验证一下以上结论。

学生亲自动手操作，验证自己的结论，教师给出必要的指导。

教师：拖动标尺，改变k的大小，猜想当k＜0时，拖动点P，P点坐标、k值、矩形OAPB的面积的变化？

学生抢答：以上结论仍然成立。

教师：真是这样吗？我们一起验证一下吧！

学生亲自动手操作，验证自己的结论，教师给出必要的指导。

教师：通过验证，k＜0时，以上结论成立吗？

学生：在拖动P点过程中P点横纵坐标的乘积不变，等于k ，矩形OAPB的面积等于。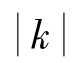

教师：综合以上两种情况，我们得出：过反比例函数图像上任何一点向两坐标轴做垂线，所构成的矩形的面积不变，等于。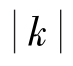

设计意图：利用超级画板合理设计，为学生创造一个动态的数学实验平台，通过亲自动手操作、增加学生学习数学的积极性。

（3）教学片段三：反比例函数与图形面积（直角三角形）

教师：类比反比例函数与矩形面积的推理过程，打开超级画板文件3，在函数图像上取一点P，过P做PA⊥x轴，链接OP，得到RtΔOPA。当k＞0时，拖动点P（或点击“动画”按钮），同学们思考在这一过程中P点坐标、k值、RtΔOPA的面积的变化？通过标尺改变k的大小，分别讨论k＞0与k＜0两种情况。

学生亲自动手操作，验证自己的结论，教师给出必要的指导。

教师：有谁能归纳自己的结论？

学生抢答：我得出：过反比例函数图像上任何一点P向一条坐标轴做垂线，连接OA所构成的RtΔOPA的面积不变，等于与。

设计意图：这里利用类比的方法，完成反比例函数与图形面积（矩形）的探究之后，放手让学生通过动手实验，通过小组合作学习总结、归纳相关知识，在理解的基础上建构新知识。

在教学过程中，通过以上三个教学片段的设计，合理地利用超级画板，为学生提供了一个动态的数学实验环境，教学中注重师生双边活动、小组交流突破难点，激发不同层次的学生积极参与数学思维活动，充分发挥学生的主体作用。及时评价学生的创新思维，让学生建立起自信心，逐次营造“会学”“乐学”的氛围来达成本课教学目标。