交互电子白板在几何概念教学中的应用效果

（一）交互式电子白板几何概念教学的优势

（1）提供多种形式的图形资源

在概念教学中，往往需要教师出示大量的图形或者模型来促进学生建立概念的抽象感官认知，交互式电子白板能够以多种形式为教师和学生提供图形资源。教师可以利用交互式电子白板的几何工具，如三角形、圆形等等，直接拖出图形，使用智能画笔画出任意需要的图形，利用直线连接成想到要形成的图形。或者利用交互式电子白板强大的资源库，在数学图库中寻找满足要求的图形，或者教师提前制作好图形放入资源库中以便上课时调用。此外，教师还可以在课前将资源准备好放到白板书写区以页面的形式保存，待上课时就可以像播放PPT那样方便地切换上下页，展示图形。

（2）可利用各种工具和软件变形图形，展示变化过程

在概念教学中，教师可能要利用之前学过的相似的图形概念来引出新的概念，这可能就需要教师在展示已学过的图形之后，通过将该相似图形变形而引出新的图形。交互式电子白板能对对象进行翻转、旋转、移动、缩放等操作，能够对用交互式电子白板工具画出的各种图形进行任意地变形。此外，通过交互式电子白板的电子笔，教师可以直接在“黑板”上对计算机进行操作，这可以使教师使用各种其他软件来实现图形的变形，比如word、几何画板等。让学生亲眼见证图形的变化过程，能帮助其找出新图形与旧图形之间的差别，从而更好地理解新的图形概念的本质。

（3）为学生提供协作探索的平台

在概念教学中，往往需要组织学生对新概念的性质进行探索。交互式电子白板能够回放所有页面的形成过程，教师可以通过带领学生回忆概念引入的过程或观看录像与学习者探讨此图形的属性特点，在观看的过程中还可以使用照相机、聚光灯等工具使学生把注意力集中在图形的某一部分或者某一处变化中，从而引导学生发现图形的性质。此外，学生还可以自己动手操作白板，来对图形进行各种操作，或与相似图形进行比较，在操作的过程中通过小组协作的方式来发现图形的各种特点。

总而言之，相比传统的多媒体，交互式电子白板不仅能提供各种平面几何教学模型资源，而且能够与其他的专业几何教学软件结合起来使用，能够满足教师对几何图形的各种操作^[9]，比如变形、删除、旋转和截取等等，在很大程度上丰富了几何概念的教学方法和手段，它的易操作性也使学生能够对几何图形进行独立的操作。最重要的是，它能够将计算机与“黑板”无缝结合，教师能够回归讲台与学生和教学内容进行交互，能大大提高对课堂的控制力和教学效果。

（二）交互式电子白板几何概念教学的流程

笔者以“再创造”理论为指导，根据几何概念教学的这几个步骤，分析每个步骤需要达到的教学目标，以最大限度发挥交互式电子白板的功能和教学效果最优化为宗旨，结合交互式电子白板的几何教学功能对几何概念的教学过程进行细化和交互式电子白板适应性调整，形成了如图3-1所示的基于交互式电子白板的几何概念教学流程，并对交互式电子白板在这个教学流程中的教学功能和所起到的教学支持作用进行了分析。

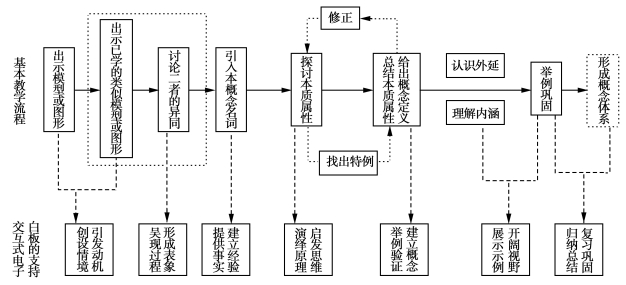
图3-1　基于交互式电子白板的几何概念教学流程

1.引入概念

几何概念教学中，概念的引入是非常重要的，特别是比较抽象又十分重要的概念。它能创设一定的学习情境，引发学习者对概念进行“再创造”的动机，使学习者形成对概念的感性认，达到对概念图形的直观思维水平，帮助学生将新知识与原有认知结构联系起来。

一般而言，引入的方法有两种，即以感性的材料引入新概念和在学生已有知识的基础上引入新概念。^[10]在几何概念教学过程中，教师可以出示符合概念的模型或图形，也可以出示已经学过的类似模型或图形，呈现概念的感性表象。

（1）出示模型或图形

在这个过程中，教师可利用交互式电子白板的几何画图功能，画出符合概念的平面几何图形，根据需要调节图形的大小和位置，还可对图形进行颜色填充等设置以吸引学习者的注意力，也可将资源库中的资源（如数学图形，图片等）调出。比如，学习平行四边形的概念之前，教师可利用几何绘图工具在白板上画出一个平行四边形或者直接从资源库中调出平行四边形的图片，也可以利用画笔工具在先在白板上画出一条线段，复制该线段后将其中一条线段平移，使两条线段平行，再画一条线段将平行的两条线段连接起来，复制这条新的线段，将复制的线段平移到两条平行线的另一端并将其连接起来，使四条线段形成首尾相接的封闭图形。

（2）出示类似模型或图形，讨论异同

若已经学过类似的概念，就可以先画出已学过的平面几何图形，再通过变形或教师用白板笔手动调整变成所教概念的图形，变形的同时要求学生说出图形是如何变化的，并利用白板的书写功能将变化过程记录下来，甚至可以利用白板的录像功能记录变化过程，让学生观看回放并总结出两种图形的异同之处。或者将已学过的图形和新授图形的同时画出来，让学习者观察总结二者的异同。比如学习平行四边形概念的定义时，可以先画出正方形图形，复制一次，再通过变形将其中一个正方形的内角大小改变，使其成为平行四边形，并与正方形相比较。(www.xing528.com)

2.明确概念

通过概念的引入对概念有了感性的认识后，应该引导学生由对概念的直观思维水平向分析和抽象思维水平转变，牢记概念名词，理解概念的本质属性。

（1）引入概念名词

教师应该准确无误地将图形的概念名词介绍给学习者，并要求他们记住。此时教师可利用白板的书写功能中的彩色笔或者特殊笔形将概念名词作为本堂课的标题写在白板上以示强调。

（2）探讨概念的属性

教师通过带领学生回忆概念引入的过程或观看录像与学习者探讨此图形的属性特点，并逐条写在白板上。教师应让学生积极发挥，不管写出的是不是该概念的本质属性，只要符合白板上所画图形的特点就应该全部记录下来。比如，画出平行四边形后，学习者可能会说平行四边形的四个角中两个是钝角，另外两个是锐角等等。

（3）给出概念的定义，总结本质属性

待学生尽述图形的特点后，教师可以给出该图形概念的定义，并在白板上用醒目的彩色笔或者特殊笔形写出，如果图形有符号表示则应把符号和图形的记法讲解透彻。比如平行四边形用符号“◇”表示，可把一个四个顶点分别标有字母A，B，C，D的平行四边形表示为◇ABCD，教师还可以用交互式电子白板的移动功能来改变顶点字母的顺序来强调强调平行四边形正确的表示方法。

为了让学生深入地了解概念，应对探讨概念属性过程中学生总结的非本质属性与本质属性区分开来，达到抽象思念水平。此时，教师可在白板上用不同的颜色建立两个不规则图形区域用来存放本质属性和非本质属性。教师通过举例将学生总结的概念的非本质属性排除，并将其移到非本质属性的颜色区域中。比如通过列举长方形或正方形两个特殊的平行四边形证明并不是所有的平行四边形都有两个钝角和两个锐角。

（4）充分理解概念内涵，认识外延

概念的定义仅仅突出了被定义的概念的最特殊的本质属性，实际上一些概念的本质并没有完全在定义中完全给出，而是以性质定理的形式表示的。要透彻地理解此概念的内涵，也要对概念的性质定理全面认识。

在总结概念的本质属性时，已经包括一部分性质定理，教师只需要将这些性质或者定理板书出来，加强学生的印象即可。但是有些性概念的某些质定理是无法直接从图形中观察出来的，比如平行四边形有一条性质为“夹在两条平行线间的平行线段相等”，需要通过教师的引导加深对概念内涵的理解。比如，在讲解平行四边形的这条性质时，教师可以用直尺工具的辅助画出两条平行线，使其夹在平行四边形的两条平行边中间，然后用直尺分别测量两条平行线的长度，并配合放大镜让学生看得更清楚，读数得出夹在平行四边形两条平行线中间的平行线段等长。当然，除了性质之外，还有一系列的判定定理来帮助学生更深入地理解几何概念的内涵。

要真正理解概念，要做到概念的内涵与外延的统一，要让学生明白概念外延包括的每一个对象都具有概念内涵所反映的所有本质属性。教师可以在白板上尽可能多地以各种形式出示属于该概念的图形，包括用几何工具画的图形、资源库中的资源和现实生活中的例子。^[11]

3.巩固概念

为了让学生更牢固地掌握所学的概念，并能正确运用该概念，应该采用多种形式复习巩固所学概念。

（1）举例巩固

图形是认识概念、复习概念和对概念进行思考的最直观的方式。教师可利用几何画图工具和资源库列举大量图形，比如标准图形、特例图形和反例图形等，要求学生依据所学概念的定义、性质和定理来做出判断。或者提出具体要求，让学生画出符合要求的图形，让学生从图形的画法中深入体会图形的性质。

（2）形成概念体系

几何图形概念实际上是成概念体系的，具有一个个的概念系列。如果能够将概念纳入概念体系，并揭示它们之间的逻辑关系，便有助于学生更加深入地认识单个概念、能使学生进一步理解单个概念的内涵。^[12]比如四边形的概念体系中就包括长方形、正方形、平行四边形、梯形、菱形等。在讲解其中某一个概念时，可用白板自带的量角器、直尺、圆规、三角板、放大器和一些外部工具等来找出这个概念和它所在的概念体系的其他图形之间的异同。